沪科版数学2023-2024学年八年级上册期中数学优质模拟卷【三】
试卷更新日期:2023-08-31 类型:期中考试
一、选择题
-
1. 在平面直角坐标系中,若点P的坐标为 , 则点P所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 在函数y= + 中,自变量x的取值范围是( )A、x<4 B、x≥4且x≠-3 C、x>4 D、x≤4且x≠-33. 等腰三角形的两条边长分别为15和7,则它的周长等于( )A、22 B、29 C、37 D、29或374. 在平面直角坐标系中,有四个点 , , , , 其中不在同一个一次函数图象上的是( )A、点A B、点B C、点C D、点D5. 下列命题属于真命题的是( )A、坐标轴上的点不属于任何象限 B、若 , 则点表示原点 C、点A、B的横坐标相同,则直线轴 D、在第四象限6. 下列说法正确的是( )A、三条线段首尾顺次相接所组成的图形叫做三角形 B、三角形按边分类可分为三边都不相等的三角形、等腰三角形和等边三角形 C、各边都相等的多边形叫正多边形 D、三角形三条中线的交点叫做三角形的重心7. 如图,直线与直线交于点 , 则关于x的不等式的解集为( )
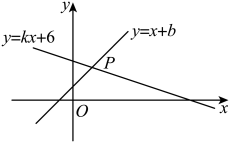 A、 B、 C、 D、8. 若函数y=kx+b由直线y=-x+2平移得到,且平移后的直线过点(2,1),则直线y=kx+b与y轴的交点坐标是( )A、(0,-3) B、(3,0) C、(1,2) D、(0,3)9. 如图,在中,点F是边 , 的垂直平分线的交点,连接 , , 若 , 则等于( )
A、 B、 C、 D、8. 若函数y=kx+b由直线y=-x+2平移得到,且平移后的直线过点(2,1),则直线y=kx+b与y轴的交点坐标是( )A、(0,-3) B、(3,0) C、(1,2) D、(0,3)9. 如图,在中,点F是边 , 的垂直平分线的交点,连接 , , 若 , 则等于( ) A、 B、 C、 D、10. 一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,两车在途中相遇时,快车恰巧出现故障,慢车继续驶往甲地,快车维修好后按原速继续行驶乙地,两车到达各地终点后停止,两车之间的距离s(km)与慢车行驶的时间t(h)之间的关系如图.下列说法正确的是( )
A、 B、 C、 D、10. 一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,两车在途中相遇时,快车恰巧出现故障,慢车继续驶往甲地,快车维修好后按原速继续行驶乙地,两车到达各地终点后停止,两车之间的距离s(km)与慢车行驶的时间t(h)之间的关系如图.下列说法正确的是( ) A、快车的速度为160km/h B、B点的坐标为 C、C点的坐标为 D、慢车出发时两车相距200km
A、快车的速度为160km/h B、B点的坐标为 C、C点的坐标为 D、慢车出发时两车相距200km二、填空题
-
11. 已知函数是一次函数,则的值为.12. 函数y=kx+b(k≠0)的图象平行于直线y=2x+3,且交y轴于点(0,-1),则其解析式是 .13. 如图,已知直线和直线交于点 , 若二元一次方程组的解为、 , 则关于.
 14. 如图, 中, , , 为线段 上一动点(不与点 , 重合),连接 ,作 , 交线段 于 .以下四个结论:
14. 如图, 中, , , 为线段 上一动点(不与点 , 重合),连接 ,作 , 交线段 于 .以下四个结论:
① ;
②当 为 中点时, ;
③当 为等腰三角形时, ;
④当 时, .
其中正确的结论是(把你认为正确结论的序号都填上),
15. 如图,在第一个△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2 , 使得A1A2=A1C,得到第二个△A1A2C;在A2C上取一点D,延长A1A2=A2D;…,按此做法进行下去,则第5个三角形中,以点A4为顶点的等腰三角形的底角的度数为.
三、作图题
-
16. 在平面直角坐标系中,三角形ABC经过平移得到三角形 . 位置如图所示.
 (1)、分别写出点A,的坐标:A , ;(2)、三角形的面积为 .(3)、若点M(m,4-n)是三角形ABC内部一点,则平移后对应点的坐标为(2m-8,n-4),求m和n的值.
(1)、分别写出点A,的坐标:A , ;(2)、三角形的面积为 .(3)、若点M(m,4-n)是三角形ABC内部一点,则平移后对应点的坐标为(2m-8,n-4),求m和n的值.四、解答题
-
17. 在平面直角坐标系中,已知点 .(1)、若点A在y轴上,求a的值;(2)、已知点 , 且直线轴,求线段的长.18. 如图: , , 若将线段平移至 , 求a与b的值.
 19. 已知一次函数 .(1)、若该函数是正比例函数,求这个一次函数的解析式;(2)、若该函数的图象经过一、二、四象限,且为整数,求这个一次函数的解析式.
19. 已知一次函数 .(1)、若该函数是正比例函数,求这个一次函数的解析式;(2)、若该函数的图象经过一、二、四象限,且为整数,求这个一次函数的解析式.五、综合题
-
20. 已知直线交x轴于点A , 交y轴于点B . 直线交x轴于点D , 与直线相交于点C .
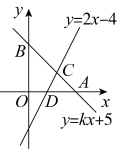 (1)、直接写出关于x的不等式的解集;(2)、求直线的解析式;(3)、求的面积.21. 如图所示,在中,平分交于点E,交于点D, , , 求的度数.
(1)、直接写出关于x的不等式的解集;(2)、求直线的解析式;(3)、求的面积.21. 如图所示,在中,平分交于点E,交于点D, , , 求的度数. 22. 为促进销售,某地水果种植户借助网络平台,在线下批发的基础上同步网络零售水果.已知销售相同数量的水果,网络零售的销售额为450元,线下批发销售额为300元,且网络零售的单价比线下批发的单价贵15元.(1)、求网络零售和线下批发水果的单价分别为每千克多少元?(2)、该种植户某天网络零售和线下批发共销售水果100千克,且网络销售的数量低于线下批发数量的2倍,设网络零售a(a为正整数)千克,获得的总销售额为W元.请写出W与a之间的函数关系式,并求出当网络销售水果的数量为多少时,当天所获得的总销售额最大?最大销售额是多少?23. 如图,直线y=-2x+7与x轴、y轴分别相交于直C、B.与直线y=x相交于点A.
22. 为促进销售,某地水果种植户借助网络平台,在线下批发的基础上同步网络零售水果.已知销售相同数量的水果,网络零售的销售额为450元,线下批发销售额为300元,且网络零售的单价比线下批发的单价贵15元.(1)、求网络零售和线下批发水果的单价分别为每千克多少元?(2)、该种植户某天网络零售和线下批发共销售水果100千克,且网络销售的数量低于线下批发数量的2倍,设网络零售a(a为正整数)千克,获得的总销售额为W元.请写出W与a之间的函数关系式,并求出当网络销售水果的数量为多少时,当天所获得的总销售额最大?最大销售额是多少?23. 如图,直线y=-2x+7与x轴、y轴分别相交于直C、B.与直线y=x相交于点A. (1)、求A点坐标;(2)、如果在y轴上存在一点P,使OAP是以OA为底边的等腰三角形,求P点坐标;(3)、在直线y=-2x+7上是否存在点Q,使OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
(1)、求A点坐标;(2)、如果在y轴上存在一点P,使OAP是以OA为底边的等腰三角形,求P点坐标;(3)、在直线y=-2x+7上是否存在点Q,使OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
-