【备考2024】2023年高考数学新高考一卷真题变式分层精准练:第4题
试卷更新日期:2023-08-31 类型:二轮复习
一、原题
-
1. 设函数在区间(0,1)单调递减,则a的取值范围是( )A、(−∞,−2] B、[−2,0) C、(0,2] D、[2,+∞)
二、基础
-
2. 下列函数中,在定义域上单调递增的是( )A、 B、 C、 D、
-
3. 下列函数中,既是偶函数又在区间上单调递增的函数是( )A、 B、 C、 D、
-
4. 已知 , 则( )A、 B、 C、 D、
-
5. 下列四个函数中,在其定义域内单调递增的是( )A、 B、 C、 D、
-
6. 下列函数中,在上为增函数的是( )A、 B、 C、 D、
-
7. 已知函数在定义域上是减函数,且 , 则实数的取值范围是( )A、 B、 C、 D、
-
8. 已知( , 且),且 , 则实数a的取值范围是( )A、0<a<1 B、a>1 C、a<1 D、a>0
-
9. 函数的单调递增区间是
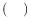 A、 B、 C、 D、
A、 B、 C、 D、 -
10. 若对任意 , 有恒成立,则实数的取值范围是( )A、 B、 C、 D、
-
11. 已知函数 , 则( )A、4 B、8 C、16 D、32
三、提高
-
12. 已知函数是上的单调函数,且 , 则在上的值域为( )A、 B、 C、 D、
-
13. 函数在区间上的图象大致为( )A、
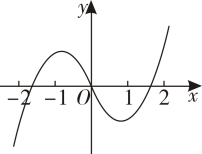 B、
B、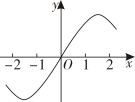 C、
C、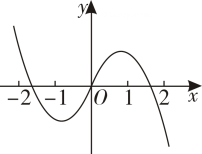 D、
D、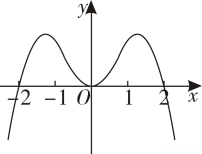
-
14. 已知 , , , 则( )A、 B、 C、 D、
-
15. 已知 , 且 , 则下列各式一定成立的是( )A、 B、 C、 D、
-
16. 已知 , 则( )A、 B、 C、 D、
-
17. 若函数在上单调,则实数的取值范围是( )A、 B、 C、 D、
-
18. 已知函数 , 若且 , 则的取值范围是( )A、 B、 C、 D、
-
19. 设函数在区间上单调递增,则的取值范围为( )A、 B、 C、 D、
-
20. 函数满足 , 当时都有 , 且对任意的 , 不等式恒成立.则实数的取值范围是
 ( ) A、 B、 C、 D、
( ) A、 B、 C、 D、
四、巅峰
-
21. 已知函数的大致图象如图所示,则的解析式可能为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
22. 已知定义在上的三个函数 , 其中为偶函数,是奇函数,且在上单调递增,在上单调递增,在上单调递减,则( )A、是奇函数,且在上单调递增 B、是偶函数,且在上单调递减 C、是奇函数,且在上单调递减 D、是偶函数,且在上单调递增
-
23. 已知函数的定义域为R,为奇函数,且对于任意 , 都有 , 则下列结论中一定成立的是( )A、 B、 C、为偶函数 D、为奇函数
-
24. 设是定义在上的奇函数,对任意的 , 满足: , 且 , 则不等式的解集为( )A、 B、 C、 D、
-
25. 已知是定义在上的函数,其导函数为 , 且不等式恒成立,则下列不等式成立的是( )A、 B、 C、 D、
