沪科版数学2023-2024学年八年级上册期中数学优质模拟卷【一】
试卷更新日期:2023-08-31 类型:期中考试
一、选择题
-
1. 已知点点 , 且直线轴,则a的值为( )A、1 B、 C、2 D、2. 已知等腰△ABC的两边长分别为2和3,则等腰△ABC的周长为( )A、7 B、8 C、6或8 D、7或83. 如图,在平面直角坐标系中,直线与直线相交于点 , 则关于 , 的二元一次方程组的解是( )
 A、 B、 C、 D、4. 下列命题为真命题的是( )A、两直线平行,同位角相等 B、实数a、b,若 , 则 C、相等的角是对顶角 D、若 , 则5. 已知点与点关于轴对称,则在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,在中, , , 直线 , 顶点在直线上,直线交于点 , 交于点 , 若 , 则的度数是( )
A、 B、 C、 D、4. 下列命题为真命题的是( )A、两直线平行,同位角相等 B、实数a、b,若 , 则 C、相等的角是对顶角 D、若 , 则5. 已知点与点关于轴对称,则在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,在中, , , 直线 , 顶点在直线上,直线交于点 , 交于点 , 若 , 则的度数是( ) A、 B、 C、 D、7. 如果关于的分式方程有非负整数解,且一次函数不经过第四象限,则所有符合条件的的和是( ).A、0 B、2 C、3 D、58. 已知一次函数和 , 则函数和的图象可能是( )A、
A、 B、 C、 D、7. 如果关于的分式方程有非负整数解,且一次函数不经过第四象限,则所有符合条件的的和是( ).A、0 B、2 C、3 D、58. 已知一次函数和 , 则函数和的图象可能是( )A、 B、
B、 C、
C、 D、
D、 9. 如图,为内一点,过点的直线与边 , 分别交于点 , , 若点 , 点恰好分别在 , 的垂直平分线上,记 , , 则 , 满足的关系式为( )
9. 如图,为内一点,过点的直线与边 , 分别交于点 , , 若点 , 点恰好分别在 , 的垂直平分线上,记 , , 则 , 满足的关系式为( ) A、 B、 C、 D、10. 已知一次函数( , k是常数),则下列结论正确的是( )A、若点在一次函数的图象上,则它的图象与两个坐标轴围成的三角形面积是2; B、若 , 则一次函数图象上任意两点和满足: C、一次函数的图象不一定经过第三象限 D、若对于一次函数和 , 无论x取任何实数,总有 , 则k的取值范围是或
A、 B、 C、 D、10. 已知一次函数( , k是常数),则下列结论正确的是( )A、若点在一次函数的图象上,则它的图象与两个坐标轴围成的三角形面积是2; B、若 , 则一次函数图象上任意两点和满足: C、一次函数的图象不一定经过第三象限 D、若对于一次函数和 , 无论x取任何实数,总有 , 则k的取值范围是或二、填空题
-
11. 将命题“线段垂直平分线上的点到线段两端的距离相等”改写成“如果……,那么……”的形式为 .12. 已知正比例函数的图象经过第二、四象限,若点在该函数的图象上,则ab.(填“>”“<”或“=”)13. 如图,在中,已知点D , E分别为边 , 中点,且的面积等于 , 则阴影部分图形面积等于 .
 14. 在平面直角坐标系中,对于点 , 我们把 叫做点 P的伴随点,已知点的伴随点为 , 点的伴随点为 , 点的伴随点为… ,这样依次得到点 , , , … ,…若 点的坐标为 , 则点的坐标为 .
14. 在平面直角坐标系中,对于点 , 我们把 叫做点 P的伴随点,已知点的伴随点为 , 点的伴随点为 , 点的伴随点为… ,这样依次得到点 , , , … ,…若 点的坐标为 , 则点的坐标为 .三、作图题
-
15. 已知中,点 , , .
 (1)、在直角坐标系中画出 , 将向右平移4个单位长度,然后再向下平移5个单位长度、得到 , 画出平移后的图形;(2)、求的面积;(3)、点在的边上,求点M′在上的对应点M的坐标.16. 在直角坐标系内,已知直线 , 请画出直线 , 并由图象解答:
(1)、在直角坐标系中画出 , 将向右平移4个单位长度,然后再向下平移5个单位长度、得到 , 画出平移后的图形;(2)、求的面积;(3)、点在的边上,求点M′在上的对应点M的坐标.16. 在直角坐标系内,已知直线 , 请画出直线 , 并由图象解答: (1)、写出方程组的解;(2)、写出不等式的解集.
(1)、写出方程组的解;(2)、写出不等式的解集.四、解答题
-
17. 已知函数(1)、若函数图象经过原点,求的值;(2)、若函数的图象平行于直线 , 求的值(3)、若这个函数是一次函数,且随着的增大而增大,且不经过第二象限,求的取值范围.18. △ABC的三边长分别为 , , .(1)、求的取值范围;(2)、若是等腰三角形,求三边长.19. 如图,已知直线:与直线平行,与x轴交于点A,与y轴交于点B.直线与y轴交于点 , 与x轴交于点D,与直线交于点.
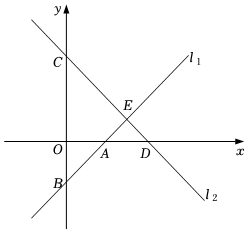 (1)、求直线对应的函数表达式;(2)、求四边形的面积.20. 如图,是的角平分线,是的边上的中线.
(1)、求直线对应的函数表达式;(2)、求四边形的面积.20. 如图,是的角平分线,是的边上的中线. (1)、若的周长为13, , , 求的长度;(2)、若 , 的面积为10, , 求点到的距离.
(1)、若的周长为13, , , 求的长度;(2)、若 , 的面积为10, , 求点到的距离.五、综合题
-
21. 小颖和小明两人分别从甲、乙两地出发骑自行车沿相同的路线相向而行,图中折线和线段分别表示小颖和小明离甲地的距离y(单位:米)与小颖行驶的时间x(单位:分)之间的函数关系图象,根据图中提供的信息,解答下列问题:
 (1)、小明骑车的速度为米/分,点C的坐标为;(2)、求线段对应的函数关系式;(3)、请直接写出小颖出发多长时间和小明相距750米.22. 阅读下列材料,并完成相应任务.
(1)、小明骑车的速度为米/分,点C的坐标为;(2)、求线段对应的函数关系式;(3)、请直接写出小颖出发多长时间和小明相距750米.22. 阅读下列材料,并完成相应任务.小学时候我们就知道三角形内角和是180度,学习了平行线之后,可以证明三角形内角和是180度,证明方法如下:
如图1,已知:三角形 ,求证 .

证法一:如图2,过点A作直线DE∥BC ,
∵ ,∴ , ,
∵ ,∴ ,
即三角形内角和是 .
证法二:如图3,延长 至M,过点C作CN∥AB ,
…
(1)、任务:(1)证法一的思路是用平行线的性质得到 , ,将三角形内角和问题转化为一个平角,进而得到三角形内角和是 ,这种方法主要体现的数学思想是(将正确选项代码填入空格处)A . 数形结合思想,B . 分类思想,C . 转化思想,D . 方程思想
(2)、将证法二补充完整.23. 等面积法是一种常用的、重要的数学解题方法. (1)、如图1,在中, , , , , , 则的长为:.(2)、如图2,在中, , , 则的高与的比是: .(3)、如图3,在中, , 点D,P分别在边 , 上,且 , , , 垂足分别为点E,F.若 , 求的值.
(1)、如图1,在中, , , , , , 则的长为:.(2)、如图2,在中, , , 则的高与的比是: .(3)、如图3,在中, , 点D,P分别在边 , 上,且 , , , 垂足分别为点E,F.若 , 求的值.