【备考2024】2023年高考数学新高考一卷真题变式分层精准练：第3题

试卷更新日期：2023-08-31 类型：二轮复习

进入出卷网下载

一、原题

1. 已知向量a=(1，1)，b=(1，−1).若(a+λb)⊥(a+µb)，则（）

A、λ+µ=1 B、λ+µ=−1 C、λµ=1 D、λµ=−1

查看试题解析

二、基础

2. 已知向量 $\vec{a} = (2 ， 1) ， \vec{b} = (m ， 1)$ ，若 $\vec{a} ⊥ \vec{b}$ ，则m为（）

A、1 B、 $\frac{1}{2}$ C、0 D、 $- \frac{1}{2}$

查看试题解析
3. 已知 $| \vec{a} | = 2 \sqrt{5}$ ， $\vec{b} = (1 ， 2)$ ， $\vec{a} / / \vec{b}$ ，则 $\vec{a} =$ （）

A、 $(2 ， 4)$ B、 $(4 ， 2)$ C、 $(2 ， - 4)$ D、 $(2 ， 4)$ 或 $(- 2 ， - 4)$

查看试题解析
4. 已知向量 $\vec{a} = (x ， 1)$ ， $\vec{b} = (1 ， - 2)$ ，且 $\vec{a} ⊥ \vec{b}$ ，则 $| \vec{a} - 2 \vec{b} | =$ （）

A、3 B、5 C、 $5 \sqrt{2}$ D、25

查看试题解析
5. 已知向量 $\vec{a} = (3 ， - 6)$ ， $\vec{b} = (2 ， λ) (λ \in R)$ ，若 $\vec{a} ⊥ \vec{b}$ ，则 $λ =$ （）

A、－4 B、－1 C、1 D、4

查看试题解析
6. 不共线的平面向量 $\overset{⇀}{a}$ ， $\overset{⇀}{b}$ 满足 ${\overset{⇀}{b}}^{2} = 2 {\overset{⇀}{a}}^{2}$ ， $(\overset{⇀}{a} + b) ⊥ \overset{⇀}{a}$ ，则平面向量 $\overset{⇀}{a}$ ， $\overset{⇀}{b}$ 的夹角为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、 $\frac{2 π}{3}$ D、 $\frac{3 π}{4}$

查看试题解析
7. 已知 $\vec{a} = (3 ， 2)$ ， $\vec{b} = (3 + m ， m + 1)$ ， $\vec{a} = λ \vec{b} (λ \in R)$ ，则m＝（）

A、－2 B、2 C、3 D、－3

查看试题解析
8. 已知向量 $\vec{a} = (1 ， 2)$ ， $\vec{b} = (- 1 ， m)$ ，若 $\vec{a} ⊥ \vec{b}$ ，则 $m$ 的值为（）

A、-2 B、 $2$ C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析

三、提高

9. 下列说法正确的是（）

A、若 $| \vec{a} | = | \vec{b} |$ ，则 $\vec{a}$ 与 $\vec{b}$ 的长度相等且方向相同或相反； B、若 $| \vec{a} | = | \vec{b} |$ ，且 $\vec{a}$ 与 $\vec{b}$ 的方向相同，则 $\vec{a} = \vec{b}$ C、平面上所有单位向量，其终点在同一个圆上； D、若 $\vec{a} / / \vec{b}$ ，则 $\vec{a}$ 与 $\vec{b}$ 方向相同或相反

查看试题解析
10. 已知向量 $\vec{a} = (2 ， - 1) ， \vec{b} = (1 ， n)$ ，若 $\vec{a} ⊥ \vec{b}$ ，则 $\vec{a} + \vec{b}$ 在 $\vec{b}$ 上的投影向量的坐标为（）

A、 $(2 ， 1)$ B、 $(- \sqrt{2} ， 1)$ C、 $(1 ， 2)$ D、 $(- 1 ， - \sqrt{2})$

查看试题解析
11. 蜜蜂的巢房是令人惊叹的神奇天然建筑物.巢房是严格的六角柱状体，它的一端是平整的六角形开口，另一端是封闭的六角菱形的底，由三个相同的菱形组成.巢中被封盖的是自然成熟的蜂蜜.如图是一个蜂巢的正六边形开口 $A B C D E F$ ，下列说法正确的是（）

A、 $\vec{A C} - \vec{A E} = \vec{B F}$ B、 $\vec{A C} + \vec{A E} = \frac{1}{2} \vec{A D}$ C、 $\vec{A D} \cdot \vec{A B} = \vec{A D} \cdot \vec{D E}$ D、 $\vec{A D} = 2 (\vec{A B} + \vec{A F})$

查看试题解析
12. 已知平面向量 $\vec{a} = (1 ， 2)$ ， $\vec{b} = (m ， 5)$ ，当 $\vec{a} + \vec{b}$ 和 $\vec{a}$ 垂直时， $\vec{a} \cdot (2 \vec{a} - 3 \vec{b}) =$ （）

A、 $- 22$ B、22 C、 $- 25$ D、25

查看试题解析
13. 已知点O是 $△ A B C$ 的内心， $A B = 4 ， A C = 3$ ， $\vec{C B} = λ \vec{C A} + μ \vec{C O}$ ，则 $λ + μ =$ （）

A、 $\frac{4}{3}$ B、 $\frac{5}{3}$ C、2 D、 $\frac{7}{3}$

查看试题解析
14. 在平行四边形 $A B C D$ 中， $\vec{B E} = \frac{1}{2} \vec{B C}$ ， $\vec{A F} = \frac{1}{3} \vec{A E}$ ．若 $\vec{A B} = m \vec{D F} + n \vec{A E}$ ，则 $m + n =$ （）

A、 $\frac{1}{2}$ B、 $\frac{3}{4}$ C、 $\frac{5}{6}$ D、 $\frac{4}{3}$

查看试题解析
15. 在△ABC中，已知 $∠ A C B = \frac{2 π}{3}$ ， $B C = 4$ ， $A C = 3$ ， D是边AB的中点，点E满足 $\vec{A E} = \frac{3}{4} \vec{A B} + \frac{1}{4} \vec{A C}$ ，则 $\vec{C D} \cdot \vec{D E} =$ （）

A、 $- \frac{5}{8}$ B、－1 C、 $\frac{1}{2}$ D、 $\frac{1}{8}$

查看试题解析
16. 已知平面向量 $\vec{a}$ ， $\vec{b}$ 满足 $(3 \vec{a} - 2 \vec{b}) ⊥ (5 \vec{a} + \vec{b})$ ，且 $\vec{a} \cdot \vec{b} = \frac{1}{7}$ ，若 $| \vec{a} | = 1$ ，则 $| \vec{b} | =$ （）

A、 $\frac{9}{2}$ B、 $\frac{15}{2}$ C、 $\sqrt{7}$ D、 $\sqrt{2}$

查看试题解析

四、巅峰

17. 如图所示，正方形 $A B C D$ 的边长为2，点 $E$ ， $F$ ， $G$ 分别是边 $B C$ ， $C D$ ， $A D$ 的中点，点 $P$ 是线段 $E F$ 上的动点，则 $\vec{G P} \cdot \vec{A P}$ 的最小值为（）

A、 $\frac{23}{8}$ B、3 C、 $\frac{27}{8}$ D、48

查看试题解析
18. 已知点 $A (- 2 ， 0) ， B ， C$ 分别为直线 $y = m x ， y = n (m ， n \in R ， m n \neq 0)$ 上的动点，若 $\vec{A B} \cdot \vec{B C} = 0$ ，则 $\vec{A B} \cdot \vec{A C}$ 的最小值为（）

A、 $n^{2}$ B、 $m n$ C、 $\frac{4 m^{2}}{m^{2} + 1}$ D、 $\frac{4 m n}{m n + 1}$

查看试题解析
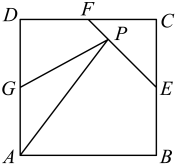19. 已知平面向量 $\vec{a} ⊥ \vec{b}$ ，且 $| \vec{c} - λ \vec{a} |$ 的最小值与 $| \vec{c} - μ \vec{b} |$ 的最小值乘积为2（ $λ ， μ$ 为实数），则 $| \vec{c} |$ 的最小值为（）

A、1 B、 $\sqrt{2}$ C、2 D、 $2 \sqrt{2}$

查看试题解析
20. 已知非零向量 $\vec{O A} ， \vec{O B} ， \vec{O C}$ ，满足 $| \vec{O A} | = 4$ ， $| \vec{O B} | = 2 | \vec{O C} |$ ，且 $3 + \vec{O A} \cdot \vec{O C} + \vec{O C} \cdot \vec{O B} = {| \vec{O C} |}^{2} + \vec{O A} \cdot \vec{O B}$ ，则 $| \vec{A B} |$ 的最小值为（）

A、 $\frac{2 \sqrt{6}}{3}$ B、3 C、 $\frac{2 \sqrt{5}}{3}$ D、1

查看试题解析
21. 如图，正方形的边长为4，剪去四个角后成为一个正八边形，则可求出此正八边形的外接圆直径 $d$ ，根据我国魏晋时期数学家刘徽的“割圆术”思想，如果用此正八边形的周长近似代替其外接圆周长，便可估计 $π$ 的值，下面 $d$ 及 $π$ 的值都正确的是（）

A、 $d = \frac{8 (\sqrt{2} - 1)}{s i n 22.5 °}$ ， $π \approx 8 s i n 22.5 °$ B、 $d = \frac{4 (\sqrt{2} - 1)}{s i n 22.5 °}$ ， $π \approx 4 s i n 22.5 °$ C、 $d = \frac{4 (\sqrt{2} - 1)}{s i n 22.5 °}$ ， $π \approx 8 s i n 22.5 °$ D、 $d = \frac{8 (\sqrt{2} - 1)}{s i n 22.5 °}$ ， $π \approx 4 s i n 22.5 °$

查看试题解析
22. 在平面中，已知单位向量 $\vec{e_{1}}$ 、 $\vec{e_{2}}$ 的夹角为 $6 0^{∘}$ ，向量 $\vec{a} = x \vec{e_{1}} + y \vec{e_{2}}$ ，且 $1 \leq x^{2} \leq 4$ ， $1 \leq y^{2} \leq 4$ ，设向量 $\vec{a}$ 与 $\vec{e_{1}}$ 的夹角为 $α$ ，则 $c o s α$ 的最大值为（）

A、 $\frac{\sqrt{6}}{4}$ B、 $\frac{\sqrt{6}}{3}$ C、 $\frac{5 \sqrt{7}}{14}$ D、 $\frac{2 \sqrt{7}}{7}$

查看试题解析
23. 已知O是 $△ A B C$ 的外心，且满足 $2 \vec{A O} = \vec{A B} + \vec{A C}$ ，若 $\vec{B A}$ 在 $\vec{B C}$ 上的投影向量为 $\frac{9}{10} \vec{B C}$ ，则 $c o s ∠ A O C =$ （）

A、 $\frac{3}{5}$ B、 $\frac{\sqrt{10}}{10}$ C、 $\frac{4}{5}$ D、 $\frac{3 \sqrt{10}}{10}$

查看试题解析
24. $\vec{e_{1}} ， \vec{e_{2}}$ 均为单位向量，且它们的夹角为45°，设 $\vec{a}$ ， $\vec{b}$ 满足 $| \vec{a} + \vec{e_{2}} | = \frac{\sqrt{2}}{4} ， \vec{b} = \vec{e_{1}} + k \vec{e_{2}} (k \in R)$ ，则 $| \vec{a} - \vec{b} |$ 的最小值为（）

A、 $\sqrt{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{2}}{4}$ D、 $\frac{3 \sqrt{2}}{4}$

查看试题解析