【备考2024年】中考数学广东卷真题变式分层精准练第6题

试卷更新日期：2023-08-30 类型：二轮复习

进入出卷网下载

一、原题

1. 我国著名数学家华罗庚曾为普及优选法作出重要贡献，优选法中有一种0.618法应用了（）

A、黄金分割数 B、平均数 C、众数 D、中位数

查看试题解析

二、基础

2. 神奇的自然界处处隐含着数学美！生物学家在向日葵圆盘中发现：向日葵籽粒成螺线状排列，螺线的发散角是 $137.5 °$ ．我们知道圆盘一周为 $360 °$ ， $360 ° - 137.5 ° = 222.5 °$ ， $137.5 ° \div 222.5 ° \approx 0.618$ ．这体现了（）

A、轴对称 B、旋转 C、平移 D、黄金分割

查看试题解析
3. 神奇的自然界处处蕴含着数学知识．动物学家在鹦鹉螺外壳上发现，其每圈螺纹的直径与相邻螺纹直径的比约为0.618．这体现了数学中的（）

A、平移 B、旋转 C、轴对称 D、黄金分割

查看试题解析
4. 若点Р是线段 $A B$ 的黄金分割点 $(A P > P B)$ ， $A B = 2$ ，则 $A P$ 的长为（）

A、 $\sqrt{5} - 1$ B、 $3 - \sqrt{5}$ C、 $\sqrt{5} + 1$ D、 $3 + \sqrt{5}$

查看试题解析
5. 比值为 $\frac{\sqrt{5} - 1}{2}$ （约0.618）的比例被公认为是最能引起美感的比例，因此被称为黄金分割比，我们中国的国旗宽与长之比就非常接近这个比例，如果某面国旗长为2米，则其宽约为（）

A、1.5米 B、1.2米 C、1.0米 D、0.8米

查看试题解析
6. 校园里一片小小的树叶，也蕴含着“黄金分割”，如图，P为AB的黄、金分割点(AP>PB)，如果AB的长度为10cm，那么AP的长度为（）cm．

A、 $\sqrt{5}$ -1 B、2 $\sqrt{5}$ -2 C、5 $\sqrt{5}$ -5 D、10 $\sqrt{5}$ -10

查看试题解析
7. 已知 $P$ 是线段 $A B$ 的黄金分割点，且 $A P > B P$ ，则下列比例式能成立的是（）

A、 $\frac{A B}{A P} = \frac{B P}{A B}$ B、 $\frac{B P}{A P} = \frac{A B}{B P}$ C、 $\frac{A P}{A B} = \frac{B P}{A P}$ D、 $\frac{A B}{A P} = \frac{\sqrt{5} - 1}{2}$

查看试题解析
8. 某品牌20寸的行李箱拉杆拉开后放置如图所示，经测量该行李箱从轮子底部到箱子上沿的高度 $A B$ 与从轮子底部到拉杆顶部的高度 $C D$ 之比是黄金比（约等于 $0.618$ ）．已知 $C D = 80$ cm，则AB约是（）

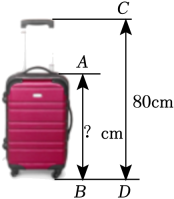A、30cm B、49cm C、55cm D、129cm

查看试题解析
9. 一般认为，如果一个人的肚脐以上的高度与肚脐以下的高度符合黄金分割，则这个人身材好．如图，是一个参加空姐选拔的选手的实际身高情况，如果要使身材好，那么她穿鞋子的高度最好为（） $c m$ ．（精确到 $1 c m$ ，参考数据：黄金分割比为 $\frac{\sqrt{5} - 1}{2} \approx 0.618$ ）

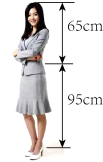A、5 B、8 C、10 D、12

查看试题解析
10. 如果一个矩形的宽与长的比等于黄金数 $\frac{\sqrt{5} - 1}{2}$ （约为0.618），就称这个矩形为黄金矩形．若矩形ABCD为黄金矩形，宽AD＝ $\sqrt{5}$ ﹣1，则长AB为（）

A、1 B、﹣1 C、2 D、﹣2

查看试题解析

三、提高

11. 如果把一条线段分为两部分，使其中较长的一段与整个线段的比是黄金分割数，那么较短一段与较长一段的比也是黄金分割数.由此，如果设整个线段长为1，较长段为x，可以列出的方程为（）

A、 $\frac{x - 1}{x}$ ＝ $\frac{x}{1}$ B、 $\frac{1 - x}{1}$ ＝ $\frac{1}{x}$ C、 $\frac{x}{1 - x}$ ＝ $\frac{1 - x}{1}$ D、 $\frac{1 - x}{x}$ ＝ $\frac{x}{\sqrt{5}}$

查看试题解析
12. 主持人在舞台上主持节目时，站在黄金分割点上，观众看上去感觉最好．若舞台长20米，主持人从舞台一侧进入，设他至少走x米时恰好站在舞台的黄金分割点上（BP长为x），则x满足的方程是（）

A、 ${(20 - x)}^{2} = 20 x$ B、 $x^{2} = 20 (20 - x)$ C、 $x (20 - x) = 2 0^{2}$ D、以上都不对

查看试题解析
13. 宽与长的比是 $\frac{\sqrt{5} - 1}{2}$ （约为0.618）的矩形叫黄金矩形，黄金矩形给我们以协调、匀称的美感．世界各国许多著名的建筑，为取得最佳的视觉效果，都采用了黄金矩形的设计，如希腊的巴特神庙等．若黄金矩形的长为 $\sqrt{5}$ ，则该黄金矩形的宽是（）

A、 $\sqrt{5} - 1$ B、 $\frac{\sqrt{5} + 1}{2}$ C、 $\frac{5 + \sqrt{5}}{2}$ D、 $\frac{5 - \sqrt{5}}{2}$

查看试题解析
14. 乐器古筝示意图如图所示，弦AB的黄金分割点C是称为玛子的支撑物，若AB=8分米，则玛子离较远的端点A的距离为（）

A、（4 $\sqrt{5}$ +4）分米 B、（4 $\sqrt{5}$ -4）分米 C、（12-4 $\sqrt{5}$ ）分米 D、（8-4 $\sqrt{5}$ ）分米

查看试题解析
15. 某校开展“展青春风采，树强国信念”科普大阅读活动．小明看到黄金分割比是一种数学上的比例关系，它具有严格的比例性、艺术性、和谐性，蕴藏着丰富的美学价值，应用时一般取0.618．特别奇妙的是在正五边形中，如图所示，连接AB，AC， $∠ A C B$ 的角平分线交边AB于点D，则点D就是线段AB的一个黄金分割点，且 $A D > B D$ ，已知 $A C = 10 c m$ ，那么该正五边形的周长为（）

A、19.1cm B、25cm C、30.9cm D、40cm

查看试题解析
16. 如图，点 $E$ 是正方形 $A B C D$ 的边 $A B$ 边上的黄金分割点，且 $A E$ ＞ $E B$ ， $S_{1}$ 表示 $A E$ 为边长的正方形面积， $S_{2}$ 表示以 $B C$ 为长， $B E$ 为宽的矩形面积， $S_{3}$ 表示正方形 $A B C D$ 除去 $S_{1}$ 和 $S_{2}$ 剩余的面积， $S_{3}$ ： $S_{2}$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、 $\frac{\sqrt{5} - 1}{2}$ D、 $\frac{3 - \sqrt{5}}{2}$

查看试题解析

四、培优

17. 如图，线段 $A B = 1$ ，在线段AB上找一点C，C把 $A B$ 分为 $A C$ 和 $B C$ 两段，其中 $A C < B C$ ，若 $\frac{A C}{C B} = \frac{C B}{A B}$ ，则点C就叫做线段 $A B$ 的黄金分割点，其中 $\frac{A C}{C B}$ （或 $\frac{C B}{A B}$ ）的值叫做黄金分割数．则黄金分割数是（）

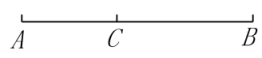A、 $\frac{\sqrt{5} + 1}{2}$ B、 $\frac{\sqrt{5} - 1}{2}$ C、 $\sqrt{5} + 1$ D、 $\sqrt{5} - 1$

查看试题解析
18. 在学习画线段 $A B$ 的黄金分割点时，小明过点B作 $A B$ 的垂线 $B C$ ，取 $A B$ 的中点M，以点B为圆心， $B M$ 为半径画弧交射线 $B C$ 于点D，连接 $A D$ ，再以点D为圆心， $D B$ 为半径画弧，前后所画的两弧分别与 $A D$ 交于E，F两点，最后，以A为圆心，“■■”的长度为半径画弧交 $A B$ 于点H，点H即为 $A B$ 的其中一个黄金分割点，这里的“■■”指的是线段（）

A、 $A F$ B、 $D F$ C、 $A E$ D、 $D E$

查看试题解析
19. 某校开展“展青春风采，树强国信念”科普阅读活动．小明看到黄金分割比是一种数学上的比例关系，它具有严格的比例性、艺术性、和谐性，蕴藏着丰富的美学价值，应用时一般取0.618．特别奇妙的是在正五边形中，如图所示，连接顶点AB，AC， $∠ A C B$ 的平分线交边AB于点D，则点D就是线段AB的一个黄金分割点，即 $\frac{A D}{A B} \approx 0.618$ ，已知 $A C = 10 c m$ ，那么该正五边形的周长为（）

A、19.1cm B、25cm C、30.9cm D、40cm

查看试题解析
20. 如图，将 $⊙ O$ 的圆周分成五等分（分点为A、B、C、D、E），依次隔一个分点相连，即成一个正五角星形.小张在制图过程中，惊讶于图形的奇妙，于是对图形展开了研究，得到：点M是线段AD、BE的黄金分割点，也是线段NE、AH的黄金分割点.在以下结论中，不正确的是（）

A、 $\frac{M N}{A M} = \frac{\sqrt{5} - 1}{2}$ B、 $\frac{F D}{A D} = \frac{\sqrt{5} - 1}{2}$ C、 $B N = N M = M E$ D、 $∠ A = 36 °$

查看试题解析