【备考2024年】中考数学杭州卷真题变式分层精准练第23题
试卷更新日期:2023-08-30 类型:二轮复习
一、原题
-
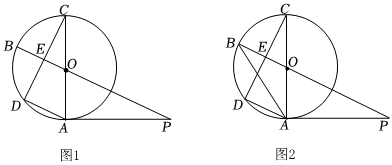
1. 如图,在中,直径垂直弦于点 , 连接 , 作于点 , 交线段于点(不与点重合),连接 .
 (1)、若 , 求的长.(2)、求证: .(3)、若 , 猜想的度数,并证明你的结论.
(1)、若 , 求的长.(2)、求证: .(3)、若 , 猜想的度数,并证明你的结论.二、基础
-
2. 如图,为的直径,D,E是上的两点,延长至点C,连接 , .
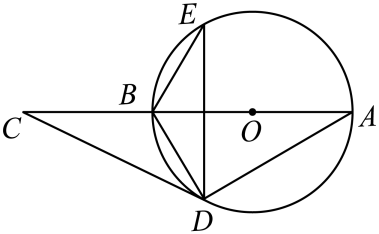 (1)、求证:;(2)、求证:是的切线;(3)、若 , 求的半径.3. 如图,为的直径,C是圆上一点,D是的中点,弦 , 垂足为点F.
(1)、求证:;(2)、求证:是的切线;(3)、若 , 求的半径.3. 如图,为的直径,C是圆上一点,D是的中点,弦 , 垂足为点F.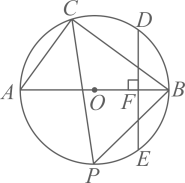 (1)、求证:;(2)、P是上一点, , 求;(3)、在(2)的条件下,当是的平分线时,求的长.4. 如图,内接于 , , 过点作的垂线,交于点 , 并与的延长线交于点 , 作 , 垂足为 , 交于点 .
(1)、求证:;(2)、P是上一点, , 求;(3)、在(2)的条件下,当是的平分线时,求的长.4. 如图,内接于 , , 过点作的垂线,交于点 , 并与的延长线交于点 , 作 , 垂足为 , 交于点 . (1)、求证:;(2)、若的半径 , , 求线段的长.5. 如图,为的直径,E为的延长线上一点,过点E作的切线,切点为点C,连接 , , 过点A作交延长线于点D.
(1)、求证:;(2)、若的半径 , , 求线段的长.5. 如图,为的直径,E为的延长线上一点,过点E作的切线,切点为点C,连接 , , 过点A作交延长线于点D. (1)、求证: .(2)、若 , , 求的长.6. 如图,已知 , 是的两条直径,直径平分 , 的一边与和直径分别交于点 , , 连接 , 且 .
(1)、求证: .(2)、若 , , 求的长.6. 如图,已知 , 是的两条直径,直径平分 , 的一边与和直径分别交于点 , , 连接 , 且 .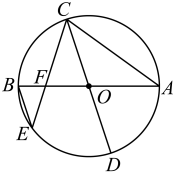 (1)、证明:;(2)、若 , 求的长.7. 如图,AB为⊙O的直径,弦CD⊥AB于点E,G为劣弧AD上一动点,AG与CD的延长线交于点F,连接AC、AD、CG、DG.记tan∠DGF=m(m为常数,且m>1).
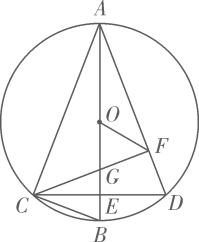
(1)、证明:;(2)、若 , 求的长.7. 如图,AB为⊙O的直径,弦CD⊥AB于点E,G为劣弧AD上一动点,AG与CD的延长线交于点F,连接AC、AD、CG、DG.记tan∠DGF=m(m为常数,且m>1).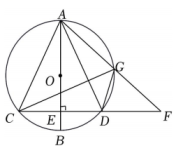 (1)、求证:∠AGC=∠ACF;(2)、求的值(用含m的式子表示).8. 如图,为的内接三角形, , 垂足为D,直径平分 , 交于点F,连结 .
(1)、求证:∠AGC=∠ACF;(2)、求的值(用含m的式子表示).8. 如图,为的内接三角形, , 垂足为D,直径平分 , 交于点F,连结 .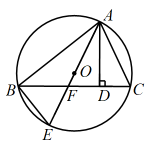 (1)、求证:;(2)、若 , 求的长;9. 如图,是的直径,C是上一点,的平分线交于E,交于 , 连接 , .
(1)、求证:;(2)、若 , 求的长;9. 如图,是的直径,C是上一点,的平分线交于E,交于 , 连接 , .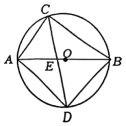 (1)、求证::(2)、若 , , 求的值.10. 如图,在中, , D是上一点,经过点A , C , D交于点E . 过点D作 , 分别交于点G , 于点F .
(1)、求证::(2)、若 , , 求的值.10. 如图,在中, , D是上一点,经过点A , C , D交于点E . 过点D作 , 分别交于点G , 于点F . (1)、求证;(2)、若 , 求的长.
(1)、求证;(2)、若 , 求的长.三、提高
-
11. 如图,在中, , 以为直径作与交于点D,过点D作 , 交延长线于点F,垂足为点E.
 (1)、求证:为的切线;(2)、若 , , 求的长.12. 如图,为的内接三角形,为延长线上一点, , 为的直径,过作交于 , 交于 , 交于 .
(1)、求证:为的切线;(2)、若 , , 求的长.12. 如图,为的内接三角形,为延长线上一点, , 为的直径,过作交于 , 交于 , 交于 . (1)、判断直线与的位置关系,并说明理由;(2)、求证:;(3)、若的直径为 . , , 求的值.13. 如图,是的直径,D是上一点,点E是的中点,过点A作的切线交的延长线于点F.连接并延长交于点C.
(1)、判断直线与的位置关系,并说明理由;(2)、求证:;(3)、若的直径为 . , , 求的值.13. 如图,是的直径,D是上一点,点E是的中点,过点A作的切线交的延长线于点F.连接并延长交于点C. (1)、求证:;(2)、如果 , , 求的长.14. 如图, 是 的直径, 是圆上的一点, 为 的中点,过点 作 的切线与 的延长线交于点 ,与 的延长线交于点 ,弦 、 交于点 .
(1)、求证:;(2)、如果 , , 求的长.14. 如图, 是 的直径, 是圆上的一点, 为 的中点,过点 作 的切线与 的延长线交于点 ,与 的延长线交于点 ,弦 、 交于点 . (1)、求证: ;(2)、求证: ;(3)、若 , ,求 的长.15. 如图,为的直径,且 , 与为圆内的一组平行弦,弦交于点H.点A在上,点B在上,.
(1)、求证: ;(2)、求证: ;(3)、若 , ,求 的长.15. 如图,为的直径,且 , 与为圆内的一组平行弦,弦交于点H.点A在上,点B在上,. (1)、求证:.(2)、求证:.(3)、在中,沿弦所在的直线作劣弧的轴对称图形,使其交直径于点G.若 , 求的长.16. 如图,点是的内心,的延长线与边相交于点 , 与的外接圆相交于点 .
(1)、求证:.(2)、求证:.(3)、在中,沿弦所在的直线作劣弧的轴对称图形,使其交直径于点G.若 , 求的长.16. 如图,点是的内心,的延长线与边相交于点 , 与的外接圆相交于点 . (1)、求证:;(2)、求证:;(3)、求证:;(4)、猜想:线段三者之间存在的等量关系.(直接写出,不需证明.)17. 如图1,在中,直径于点F,点E为上一点,点C为弧的中点,连接 , 交于点G.
(1)、求证:;(2)、求证:;(3)、求证:;(4)、猜想:线段三者之间存在的等量关系.(直接写出,不需证明.)17. 如图1,在中,直径于点F,点E为上一点,点C为弧的中点,连接 , 交于点G. (1)、求证:;(2)、如图2,过点C作的切线交BA的延长线于点Q,若 , , 求的长度;(3)、在(2)的基础上,点P为上任一点,连接 , 的比值是否发生改变?若不变,求出比值;若变化,说明变化规律.
(1)、求证:;(2)、如图2,过点C作的切线交BA的延长线于点Q,若 , , 求的长度;(3)、在(2)的基础上,点P为上任一点,连接 , 的比值是否发生改变?若不变,求出比值;若变化,说明变化规律.四、培优
-
18. 如图1,为的对角线,的外接圆交于点 , 连结 .
 (1)、求证∶ .(2)、如图2,当时,连结 , 延长交于点 , 求证 .(3)、如图3,在(2)的条件下,记的交点为点 , 连结 .
(1)、求证∶ .(2)、如图2,当时,连结 , 延长交于点 , 求证 .(3)、如图3,在(2)的条件下,记的交点为点 , 连结 .①求证∶ .
②当时,求的值.
19. 如图,内接于圆O, , 点D为劣弧上动点,延长 , 交于点E,作交圆O于点F,连接 . (1)、如图1,当点D为弧的中点时,求证:;(2)、如图2,若 , , 试用含有的代数式表示;(3)、在(2)的条件下,若 .
(1)、如图1,当点D为弧的中点时,求证:;(2)、如图2,若 , , 试用含有的代数式表示;(3)、在(2)的条件下,若 .①求证:;
②求的值.
20. 如图,内接于 , 且 , . 是劣弧上一点,分别交 , 于点 , 点 , 交于点 . (1)、当经过圆心时,
(1)、当经过圆心时,①求证:平分;
②求的值;
(2)、①连接 , 求证:;②连接 , 求证:;
③连接 , 若 , 求的长.
 21. 如图1:以x轴的正半轴上一点O1为圆心作⊙O1 , 交x轴于C、D两点,交y轴于A、B两点,以O为圆心OA为半径的⊙O与x轴的负半轴交于G点.设⊙O1的弦AC的延长线交⊙O于F点,连结GF,AG,若AO=4,
21. 如图1:以x轴的正半轴上一点O1为圆心作⊙O1 , 交x轴于C、D两点,交y轴于A、B两点,以O为圆心OA为半径的⊙O与x轴的负半轴交于G点.设⊙O1的弦AC的延长线交⊙O于F点,连结GF,AG,若AO=4, (1)、求证:△AGC∽△AFG;(2)、求出点O1的坐标;(3)、如图2,线段EA、EB(或它们的延长线)分别交⊙O于点M、N.问:当点E在(不含端点A、B)上运动时,线段MN的长度是否会发生变化?若不变,求出MN的长度;若变化,请说明理由.22.
(1)、求证:△AGC∽△AFG;(2)、求出点O1的坐标;(3)、如图2,线段EA、EB(或它们的延长线)分别交⊙O于点M、N.问:当点E在(不含端点A、B)上运动时,线段MN的长度是否会发生变化?若不变,求出MN的长度;若变化,请说明理由.22.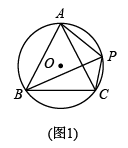

 (1)、【证明体验】
(1)、【证明体验】
如图1,是等腰的外接圆, , 在上取一点 , 连结 , 求证:;(2)、【思考探究】
如图2,在(1)条件下,若点为的中点, , 求的值;(3)、【拓展延伸】
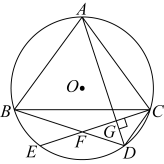
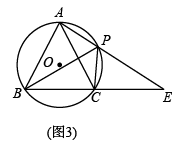
如图3,的半径为5,弦 , 弦 , 延长交的延长线于点 , 且 , 求的值.23. A,B在半径为的上, , C在劣弧上,、延长线交于点D,连结. (1)、求的度数;(2)、若 , , 求y与x的关系式;(3)、 , 以M为圆心的圆经过点A,C.当时,求的半径.
(1)、求的度数;(2)、若 , , 求y与x的关系式;(3)、 , 以M为圆心的圆经过点A,C.当时,求的半径.
-