【备考2024年】中考数学杭州卷真题变式分层精准练第20题
试卷更新日期:2023-08-30 类型:二轮复习
一、原题
-
1. 在直角坐标系中,已知 , 设函数与函数的图象交于点和点 . 已知点的横坐标是2,点的纵坐标是 .
 (1)、求的值.(2)、过点作轴的垂线,过点作轴的垂线,在第二象限交于点;过点作轴的垂线,过点作轴的垂线,在第四象限交于点 . 求证:直线经过原点.
(1)、求的值.(2)、过点作轴的垂线,过点作轴的垂线,在第二象限交于点;过点作轴的垂线,过点作轴的垂线,在第四象限交于点 . 求证:直线经过原点.二、基础
-
2. 如图,一次函数的图象与反比例函数的图象相交于两点,与轴相交于点 .
 (1)、求一次函数与反比例函数的解析式;(2)、若点与点关于轴对称,求的面积.3. 已知反比例函数 , 点都在该反比例函数图象上.
(1)、求一次函数与反比例函数的解析式;(2)、若点与点关于轴对称,求的面积.3. 已知反比例函数 , 点都在该反比例函数图象上. (1)、求反比例函数的表达式;(2)、当时,直接写出y的取值范围;(3)、若经过的直线与y轴交于点C,求的面积.4. 已知反比例函数的图象与一次函数的图象交于点 .(1)、求反比例函数的表达式;(2)、点A先往左平移n个单位,再往下平移6个单位后落在反比例函数的图象上,求n的值.5. 如图所示,一次函数的图象与反比例函数交于 , 两点.(1)、求反比例函数的表达式;(2)、写出当一次函数大于反比例函数时,的取值范围.6. 如图,一次函数与反比例函数的图象交于点 , .
(1)、求反比例函数的表达式;(2)、当时,直接写出y的取值范围;(3)、若经过的直线与y轴交于点C,求的面积.4. 已知反比例函数的图象与一次函数的图象交于点 .(1)、求反比例函数的表达式;(2)、点A先往左平移n个单位,再往下平移6个单位后落在反比例函数的图象上,求n的值.5. 如图所示,一次函数的图象与反比例函数交于 , 两点.(1)、求反比例函数的表达式;(2)、写出当一次函数大于反比例函数时,的取值范围.6. 如图,一次函数与反比例函数的图象交于点 , .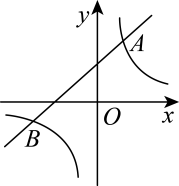 (1)、求反比例函数和一次函数的表达式.(2)、根据图象,当x取何值时,一次函数的值大于反比例函数的值?7. 如图,在平面直角坐标系中,直线与轴交于点 , 与反比例函数在第二象限内的图象相交于点 .
(1)、求反比例函数和一次函数的表达式.(2)、根据图象,当x取何值时,一次函数的值大于反比例函数的值?7. 如图,在平面直角坐标系中,直线与轴交于点 , 与反比例函数在第二象限内的图象相交于点 .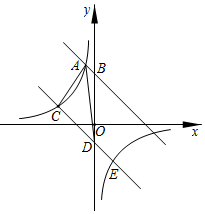 (1)、求直线的解析式;(2)、将直线向下平移个单位后与反比例函数的图象交于点和点 , 与轴交于点 , 求的面积;(3)、设直线的解析式为 , 根据图象直接写出不等式的解集.8. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于、两点.
(1)、求直线的解析式;(2)、将直线向下平移个单位后与反比例函数的图象交于点和点 , 与轴交于点 , 求的面积;(3)、设直线的解析式为 , 根据图象直接写出不等式的解集.8. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于、两点. (1)、求一次函数和反比例函数的解析式;(2)、直接写出当时,自变量x的取值范围.(3)、若P是y轴上一点,且满足的面积是10,请求出点P的坐标.9. 如图,在平面直角坐标系中,直线与x轴、y轴分别交于F,E两点,与反比例函数的图象交于点和点 .
(1)、求一次函数和反比例函数的解析式;(2)、直接写出当时,自变量x的取值范围.(3)、若P是y轴上一点,且满足的面积是10,请求出点P的坐标.9. 如图,在平面直角坐标系中,直线与x轴、y轴分别交于F,E两点,与反比例函数的图象交于点和点 . (1)、求反比例函数解析式和B点坐标;(2)、如图,连接 , P为线段上一点,使得 , 求P点坐标.10. 如图,一次函数的图象与反比例函数的图象相交于点 , 两点.
(1)、求反比例函数解析式和B点坐标;(2)、如图,连接 , P为线段上一点,使得 , 求P点坐标.10. 如图,一次函数的图象与反比例函数的图象相交于点 , 两点. (1)、分别求出一次函数和反比例函数的解析式;(2)、根据图象,直接写出满足的x的取值范围;(3)、连接并延长交双曲线于点C,连接 , 求的面积.
(1)、分别求出一次函数和反比例函数的解析式;(2)、根据图象,直接写出满足的x的取值范围;(3)、连接并延长交双曲线于点C,连接 , 求的面积.三、提高
-
11. 一次函数与反比例函数的图象交于 , 两点,点的坐标为 .
 (1)、求一次函数和反比例函数的表达式;(2)、求的面积;(3)、过动点作轴的垂线 , 与一次函数和反比例函数的图象分别交于 , 两点,当在的上方时,请直接写出的取值范围.12. 如图,在平面直角坐标系中,矩形的两个顶点A,点B分别在x轴,y轴上,已知点A为 , , 点D是边的中点,反比例函数的图象经过点D,交边于点E,直线的解析式为 . 点M在反比例函数图象上,过点M作x轴的垂线交直线于点N.
(1)、求一次函数和反比例函数的表达式;(2)、求的面积;(3)、过动点作轴的垂线 , 与一次函数和反比例函数的图象分别交于 , 两点,当在的上方时,请直接写出的取值范围.12. 如图,在平面直角坐标系中,矩形的两个顶点A,点B分别在x轴,y轴上,已知点A为 , , 点D是边的中点,反比例函数的图象经过点D,交边于点E,直线的解析式为 . 点M在反比例函数图象上,过点M作x轴的垂线交直线于点N. (1)、求反比例函数的解析式和直线的解析式;(2)、连接 , 是否存在点M,使得以C,D,M,N为顶点的四边形为平行四边形?若存在,求点M的坐标;若不存在,请说明理由.13. 如图,一次函数与函数为的图象交于两点.
(1)、求反比例函数的解析式和直线的解析式;(2)、连接 , 是否存在点M,使得以C,D,M,N为顶点的四边形为平行四边形?若存在,求点M的坐标;若不存在,请说明理由.13. 如图,一次函数与函数为的图象交于两点. (1)、求这两个函数的解析式;(2)、根据图象,直接写出满足时x的取值范围;(3)、点P在线段上,过点P作x轴的垂线,垂足为M,交函数的图象于点Q,若面积为3,求点P的坐标.14. 如图,点A在反比例函数的图象上,轴于点B, , .
(1)、求这两个函数的解析式;(2)、根据图象,直接写出满足时x的取值范围;(3)、点P在线段上,过点P作x轴的垂线,垂足为M,交函数的图象于点Q,若面积为3,求点P的坐标.14. 如图,点A在反比例函数的图象上,轴于点B, , . (1)、求反比例函数的解析式;(2)、点C在这个反比例函数图象上,连接并延长交x轴于点D,且 , 求点C的坐标.15. 如图,正比例函数与反比例函数的图象交于、两点,的横坐标为 , 的纵坐标为 .
(1)、求反比例函数的解析式;(2)、点C在这个反比例函数图象上,连接并延长交x轴于点D,且 , 求点C的坐标.15. 如图,正比例函数与反比例函数的图象交于、两点,的横坐标为 , 的纵坐标为 .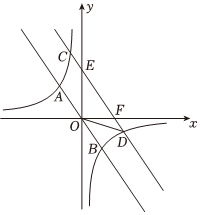 (1)、求反比例函数的表达式.(2)、观察图象,直接写出不等式的解集.(3)、将直线向上平移个单位,交双曲线于、两点,交坐标轴于点、 , 连接、 , 若的面积为 , 求直线的表达式.16. 如图,一次函数的图象与反比例函数的图象分别交于点 , 点 , 与轴,轴分别交于点 , 点 , 作轴,垂足为点 , .
(1)、求反比例函数的表达式.(2)、观察图象,直接写出不等式的解集.(3)、将直线向上平移个单位,交双曲线于、两点,交坐标轴于点、 , 连接、 , 若的面积为 , 求直线的表达式.16. 如图,一次函数的图象与反比例函数的图象分别交于点 , 点 , 与轴,轴分别交于点 , 点 , 作轴,垂足为点 , .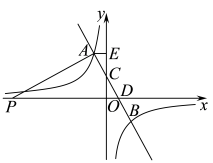 (1)、求反比例函数的表达式;(2)、在第二象限内,当时,直接写出的取值范围;(3)、点在轴负半轴上,连接 , 且 , 求点坐标.
(1)、求反比例函数的表达式;(2)、在第二象限内,当时,直接写出的取值范围;(3)、点在轴负半轴上,连接 , 且 , 求点坐标.四、培优
-
17. 如图,菱形的边在轴上,点A的坐标为 , 点在反比例函数的图象上,直线经过点 , 与轴交于点 , 连接 .
 (1)、求的值.(2)、求的面积.(3)、已知点在反比例函数的图象上,点的横坐标为 . 若 , 则的取值范围为 .18. 如图,在平面直角坐标系中,直线l:与x轴、y轴分别交于点A、B,与双曲线相交于点C,点C在第二象限且的面积为20.点在双曲线上.
(1)、求的值.(2)、求的面积.(3)、已知点在反比例函数的图象上,点的横坐标为 . 若 , 则的取值范围为 .18. 如图,在平面直角坐标系中,直线l:与x轴、y轴分别交于点A、B,与双曲线相交于点C,点C在第二象限且的面积为20.点在双曲线上.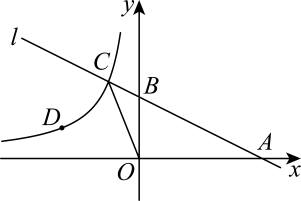 (1)、求点C的坐标以及k的值;(2)、联结 , 直线l向上平移交直线于点P,点Q为平面内任意一点,如果四边形为菱形,求点P的坐标;(3)、点E为y轴上一动点,联结 , 以为边向右侧作正方形 , 在点E运动的过程中,当顶点F落在直线上时,求点E的坐标.19. 定义:把能被一条对角线分成两个全等直角三角形的四边形叫做勾股四边形.(1)、矩形勾股四边形(填“是”或“不是”).(2)、如图在直角坐标系中,直线y=-x+1与双曲线相交于A,B两点,点在x轴负半轴上,Q为直角坐标平面上一点.
(1)、求点C的坐标以及k的值;(2)、联结 , 直线l向上平移交直线于点P,点Q为平面内任意一点,如果四边形为菱形,求点P的坐标;(3)、点E为y轴上一动点,联结 , 以为边向右侧作正方形 , 在点E运动的过程中,当顶点F落在直线上时,求点E的坐标.19. 定义:把能被一条对角线分成两个全等直角三角形的四边形叫做勾股四边形.(1)、矩形勾股四边形(填“是”或“不是”).(2)、如图在直角坐标系中,直线y=-x+1与双曲线相交于A,B两点,点在x轴负半轴上,Q为直角坐标平面上一点.
①分别求出A、B两点的坐标.
②当四边形是平行四边形时,如图,请证明是勾股四边形.
(3)、在(2)的条件下,当以A、B、P、Q为顶点的四边形是勾股四边形时,请直接写出Q点的坐标.20. 如图,直线分别与反比例函数和的图象交于A,B两点,点B横坐标为2. (1)、求n的值.(2)、若点C为图像上一点,过点C作直线轴,交反比例函数于点D,当时,求C点横坐标.(3)、若点E在直线AB上,请在坐标平面内找一点F,使得以C,D,E,F四点为顶点的四边形是正方形,并求出点F的坐标.21. 如图1,在平面直角坐标系中,点 , 点 , 直线与反比例函数的图象在第一象限交于点 .
(1)、求n的值.(2)、若点C为图像上一点,过点C作直线轴,交反比例函数于点D,当时,求C点横坐标.(3)、若点E在直线AB上,请在坐标平面内找一点F,使得以C,D,E,F四点为顶点的四边形是正方形,并求出点F的坐标.21. 如图1,在平面直角坐标系中,点 , 点 , 直线与反比例函数的图象在第一象限交于点 . (1)、求反比例函数的解析式(2)、如图2,点是反比例函数图象上一点,连接 , 。试问在轴上是否存在一点 , 使△ACD的面积与△ACE的面积相等,若存在,请求出点的坐标;若不存在,请说明理由。(3)、在(2)的条件下,坐标原点O关于点的对称点为 , 且点在轴的正半轴上,若点是反比例函数的第一象限图象上一个动点,连接MG,以MG为边作正方形 , 当顶点恰好落在直线上时,求点M的坐标。22. 我们定义:如果一个矩形周长和面积都是矩形的倍,那么我们就称矩形是矩形的完全倍体.(1)、若矩形为正方形,是否存在一个正方形是正方形的完全倍体?(填“存在”或“不存在”).(2)、【深入探究】长为 , 宽为的矩形是否存在完全倍体?
(1)、求反比例函数的解析式(2)、如图2,点是反比例函数图象上一点,连接 , 。试问在轴上是否存在一点 , 使△ACD的面积与△ACE的面积相等,若存在,请求出点的坐标;若不存在,请说明理由。(3)、在(2)的条件下,坐标原点O关于点的对称点为 , 且点在轴的正半轴上,若点是反比例函数的第一象限图象上一个动点,连接MG,以MG为边作正方形 , 当顶点恰好落在直线上时,求点M的坐标。22. 我们定义:如果一个矩形周长和面积都是矩形的倍,那么我们就称矩形是矩形的完全倍体.(1)、若矩形为正方形,是否存在一个正方形是正方形的完全倍体?(填“存在”或“不存在”).(2)、【深入探究】长为 , 宽为的矩形是否存在完全倍体?小鸣和小棋分别有以下思路:
【小鸣方程流】设新矩形长和宽为、 , 则依题意 ,
联立得 , 再探究根的情况;
【小棋函数流】如图,也可用反比例函数:与一次函数:来研究,作出图象,有交点,意味着存在完全倍体.

那么长为4.宽为3的矩形是否存在完全倍体?请利用上述其中一种思路说明原因.(3)、如果长为4,宽为3的矩形存在完全倍体,请求出的取值范围。
-