【备考2024年】中考数学杭州卷真题变式分层精准练第19题
试卷更新日期:2023-08-30 类型:二轮复习
一、原题
-
1. 如图,平行四边形的对角线相交于点 , 点在对角线上,且 , 连接 , .
 (1)、求证:四边形是平行四边形.(2)、若的面积等于2,求的面积.
(1)、求证:四边形是平行四边形.(2)、若的面积等于2,求的面积.二、基础
-
2. 如图,在平行四边形中,点E,F对角线上,且 , 连接、、、、求证:四边形是平行四边形.
 3. 如图,在中,点E在上,点F在上,且 .
3. 如图,在中,点E在上,点F在上,且 .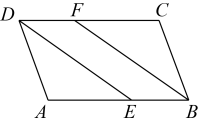 (1)、求证:四边形是平行四边形;(2)、若为的平分线,且 , , 求的周长.4. 如图,四边形对角线交于点 , 且为中点,点、在直线上, , . 求证:四边形是平行四边形.
(1)、求证:四边形是平行四边形;(2)、若为的平分线,且 , , 求的周长.4. 如图,四边形对角线交于点 , 且为中点,点、在直线上, , . 求证:四边形是平行四边形. 5. 如图,在中,对角线 , 相交于点O , 点E , F在上,点G , H在上,且 , .
5. 如图,在中,对角线 , 相交于点O , 点E , F在上,点G , H在上,且 , .
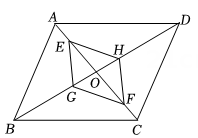 (1)、若 , , 试求的度数.(2)、求证:四边形是平行四边形.6. 如图,点B是的边上的定点,点C是边上的动点,将绕点B逆时针旋转得到 , 且点A的对应点D恰好落在边上,连接 . 点F是上一点,连接 , 且点F到的距离等于点F到的距离.当时.
(1)、若 , , 试求的度数.(2)、求证:四边形是平行四边形.6. 如图,点B是的边上的定点,点C是边上的动点,将绕点B逆时针旋转得到 , 且点A的对应点D恰好落在边上,连接 . 点F是上一点,连接 , 且点F到的距离等于点F到的距离.当时. (1)、求证:四边形是平行四边形;(2)、若 , 求的度数.7. 如图,等边的边长是4,D、E分别为、的中点,过E点作交的延长线于点F,连接 .
(1)、求证:四边形是平行四边形;(2)、若 , 求的度数.7. 如图,等边的边长是4,D、E分别为、的中点,过E点作交的延长线于点F,连接 . (1)、求证:四边形平行四边形;(2)、求的长.8. 如图,点B是的边上的定点,点C是边上的动点,将绕点B逆时针旋转得到 , 且点A对应点D恰好落在边上,连接 . 点F是上一点,连接 , 且点F到的距离等于点F到的距离.当时.
(1)、求证:四边形平行四边形;(2)、求的长.8. 如图,点B是的边上的定点,点C是边上的动点,将绕点B逆时针旋转得到 , 且点A对应点D恰好落在边上,连接 . 点F是上一点,连接 , 且点F到的距离等于点F到的距离.当时. (1)、求证:四边形是平行四边形;(2)、若 , 求度数.9. 如图,在四边形中, , 点在边上, , , 垂足为 .
(1)、求证:四边形是平行四边形;(2)、若 , 求度数.9. 如图,在四边形中, , 点在边上, , , 垂足为 .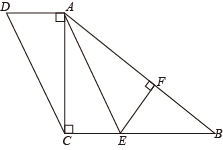 (1)、求证:四边形是平行四边形;(2)、若平分 , , , 求和的长.10. 如图,在中, , D为边上一点,连接 , E为中点,过点C作交BE的延长线于F,连接交于点G,连接 .
(1)、求证:四边形是平行四边形;(2)、若平分 , , , 求和的长.10. 如图,在中, , D为边上一点,连接 , E为中点,过点C作交BE的延长线于F,连接交于点G,连接 . (1)、求证:四边形是平行四边形;(2)、若 , , , 求四边形的面积.
(1)、求证:四边形是平行四边形;(2)、若 , , , 求四边形的面积.三、提高
-
11. 如图,点 , , , 在同一条直线上,点 , 分别在直线的两侧,且 , , .
 (1)、求证:四边形是平行四边形(2)、若四边形是菱形, , , , 求的长.12. 如图,是的中线,是线段上一点(不与点重合).交于点 , , 连接 .
(1)、求证:四边形是平行四边形(2)、若四边形是菱形, , , , 求的长.12. 如图,是的中线,是线段上一点(不与点重合).交于点 , , 连接 . (1)、如图1,当点与重合时,证明;(2)、如图1,当点与重合时,求证:四边形是平行四边形;(3)、如图2,当点不与重合时,(2)中的结论还成立吗?请说明理由.13. 如图,在中, , 点E是的中点,的平分线交于点D , 作 , 连接并延长交于点F , 连接 .
(1)、如图1,当点与重合时,证明;(2)、如图1,当点与重合时,求证:四边形是平行四边形;(3)、如图2,当点不与重合时,(2)中的结论还成立吗?请说明理由.13. 如图,在中, , 点E是的中点,的平分线交于点D , 作 , 连接并延长交于点F , 连接 . (1)、求证:四边形是平行四边形;(2)、当时,请判断四边形的形状,并说明理由.14. 如图,已知是等边三角形,点是边上的一点.
(1)、求证:四边形是平行四边形;(2)、当时,请判断四边形的形状,并说明理由.14. 如图,已知是等边三角形,点是边上的一点. (1)、求作:直线 , 使于点(要求:尺规作图,保留作图痕迹,不写作法);(2)、在(1)所作图中,取边上的点 , 使 , 连接 , . 若 , 请按要求补全图形,并证明四边形是平行四边形(若完成第(1)题有困难,可画草图完成第(2)题).15. 如图,在中, , 分别是边 , 的中点,过点作交延长线于点 , 连接 , .
(1)、求作:直线 , 使于点(要求:尺规作图,保留作图痕迹,不写作法);(2)、在(1)所作图中,取边上的点 , 使 , 连接 , . 若 , 请按要求补全图形,并证明四边形是平行四边形(若完成第(1)题有困难,可画草图完成第(2)题).15. 如图,在中, , 分别是边 , 的中点,过点作交延长线于点 , 连接 , . (1)、求证:四边形为平行四边形;(2)、请对的边或角添加一个条件,使得四边形成为菱形,并进行证明.16. 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连结CF.
(1)、求证:四边形为平行四边形;(2)、请对的边或角添加一个条件,使得四边形成为菱形,并进行证明.16. 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连结CF.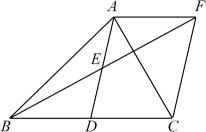 (1)、求证:① △AEF≌△DEB;② 四边形ADCF是平行四边形;(2)、若AB=AC,试判断四边形ADCF的形状,并证明你的结论.
(1)、求证:① △AEF≌△DEB;② 四边形ADCF是平行四边形;(2)、若AB=AC,试判断四边形ADCF的形状,并证明你的结论.四、培优
-
17. 如图,在中,且分别交对角线于点E、F , 连接 .
 (1)、求证:四边形是平行四边形;(2)、若 , , , 求的长.(3)、在(2)的条件下,求四边形的面积.18. 综合与实践:如图,在中,的平分线交边于点 , 交边的延长线于点 .
(1)、求证:四边形是平行四边形;(2)、若 , , , 求的长.(3)、在(2)的条件下,求四边形的面积.18. 综合与实践:如图,在中,的平分线交边于点 , 交边的延长线于点 .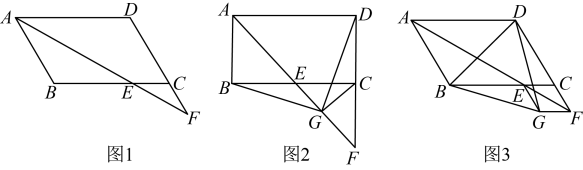 (1)、如图1,求证:;(2)、如图2,若 , 是的中点,分别连接 , , , 求证:;(3)、如图3,若 , 四边形为平行四边形,分别连接 , , , 请直接判断的形状.19. “先天下之忧而忧,后天下之乐而乐”这是《岳阳楼记》中的一句千古名言,也是岳阳精神的真实写照,这句话具有鲜明的对称美.如果一个凸四边形沿着它的一条对角线对折后能完全重合,我们就把这个四边形称为“忧乐四边形”.如图1,凸四边形沿对角线对折后完全重合,四边形是以直线为对称轴的“忧乐四边形”.
(1)、如图1,求证:;(2)、如图2,若 , 是的中点,分别连接 , , , 求证:;(3)、如图3,若 , 四边形为平行四边形,分别连接 , , , 请直接判断的形状.19. “先天下之忧而忧,后天下之乐而乐”这是《岳阳楼记》中的一句千古名言,也是岳阳精神的真实写照,这句话具有鲜明的对称美.如果一个凸四边形沿着它的一条对角线对折后能完全重合,我们就把这个四边形称为“忧乐四边形”.如图1,凸四边形沿对角线对折后完全重合,四边形是以直线为对称轴的“忧乐四边形”.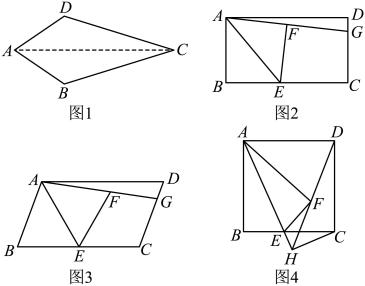 (1)、下列四边形一定是“忧乐四边形”的有(填序号)
(1)、下列四边形一定是“忧乐四边形”的有(填序号)①平行四边形;②长方形;③正方形;④菱形;⑤梯形
(2)、在四边形中,点E是边上的中点,四边形是以直线为对称轴的“忧乐四边形”(点F在四边形内部),连接并延长交于点G .①如图2,若四边形是矩形,求证:四边形是“忧乐四边形”.
②如图3,若四边形是平行四边形,①中的结论是否仍然成立,请说明理由.
(3)、如图4,四边形是正方形,且点E为线段上的动点(不与B、C重合),四边形是以直线为对称轴的“忧乐四边形”(点F在正方形内部),连接并延长,与的延长线交于点H , 连接 , 请直接写出三条线段之间的数量关系.20. 综合与实践如图1,在正方形中,点 , 分别是边 , 上的点,且 .
 (1)、求证: .(2)、如图2,在图1的基础上,过点作的垂线,与正方形的外角的平分线交于点 , 连接 . 求证:四边形是平行四边形.(提示:在上截取 , 连接)(3)、如图3,连接 , 若四边形的面积是9, , 则直接写出的长.21. 综合与探究
(1)、求证: .(2)、如图2,在图1的基础上,过点作的垂线,与正方形的外角的平分线交于点 , 连接 . 求证:四边形是平行四边形.(提示:在上截取 , 连接)(3)、如图3,连接 , 若四边形的面积是9, , 则直接写出的长.21. 综合与探究如图,直线分别交轴,轴于点 , 过点A作直线分别交轴,轴于点 , .
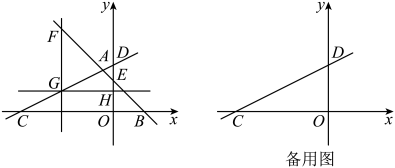 (1)、求直线的解析式.(2)、在轴左侧作直线轴,分别交直线 , 于点 . 当时,过点作直线轴,交轴于点 . 能否在直线上找一点 , 使的值最小,求出点的坐标.(3)、为直线上一点,在(2)的条件下,轴上是否存在点使得以为顶点的四边形为平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.22. 综合与实践(1)、问题情境:
(1)、求直线的解析式.(2)、在轴左侧作直线轴,分别交直线 , 于点 . 当时,过点作直线轴,交轴于点 . 能否在直线上找一点 , 使的值最小,求出点的坐标.(3)、为直线上一点,在(2)的条件下,轴上是否存在点使得以为顶点的四边形为平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.22. 综合与实践(1)、问题情境:
在综合实践活动课上,同学们以“平行四边形纸片的折叠”为主题开展数学活动.在平行四边形纸片中,E为边上任意一点,将沿折叠,点D的对应点为 .

分析探究:
如图1,当点恰好落在边上时,四边形的形状为 .(2)、问题解决:
如图2,当E,F为边的三等分点时,连接并延长,交边于点G.试判断线段与的数量关系,并说明理由.(3)、如图3,当 , 时,连接并延长,交边于点H.若的面积为24, , 请直接写出线段的长.
-