四川省达州市开江县2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-08-29 类型：期末考试

进入出卷网下载

一、单选题

1. 下列计算中正确的是（）

A、 $a^{3} \cdot a^{4} = a^{12}$ B、 ${(a^{3})}^{4} = a^{7}$ C、 $a^{3} + a^{3} = a^{6}$ D、 $a^{8} \div a^{4} = a^{4}$

查看试题解析
2. 2023年5月30日9时31分，搭载神舟十六号载人飞船的长征二号F遥十六运载火箭在酒泉卫星发射中心发射升空，跑好星辰大海中的新接力．下列图形是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 纳米是非常小的长度单位，把长为2纳米的物体放在乒乓球上，就如同把乒乓球放在地球上.2纳米=0.000000002米，0.000000002这个数用科学记数法表示为（）

A、 $20 \times 1 0^{- 10}$ B、 $0.2 \times 1 0^{- 8}$ C、 $2 \times 1 0^{- 9}$ D、 $0.02 \times 1 0^{- 7}$

查看试题解析
4. 下列事件中，属于必然事件的是（）

A、在一张纸上任意画两条线段，这两条线段相交 B、若a是有理数，则 $| a | \geq 0$ C、篮球队员在罚球线上投篮一次，未投中 D、两个负数的和为正数

查看试题解析
5. 如图，要测量河中礁石A离岸边B点的距离，可以采用如下方法：顺着河岸方向任取一条线段 $B C$ ，作 $∠ C B A^{^{'}} = ∠ C B A$ ， $∠ B C A^{'} = ∠ B C A$ ，可得 $△ A^{'} B C ≌ △ A B C$ ，所以 $A^{'} B = A B$ ，所以测量 $A^{'} B$ 的长就是礁石A离岸边B点的距离．判定两个三角形全等的理由是（）

A、 $S S S$ B、 $A A S$ C、 $S A S$ D、 $A S A$

查看试题解析
6. 已知 $a ∥ b$ ，将一个等腰直角三角板按图所示方式摆放．若 $∠ 2 = 30 °$ ，则 $∠ 1$ 的度数为（）

A、 $10 °$ B、 $15 °$ C、 $20 °$ D、 $25 °$

查看试题解析
7. 如图是一张直角三角形纸片 $A B C$ ， $∠ C = 90 °$ ， $∠ B = 40 °$ ，将 $△ A B C$ 折叠使点B和点A重合，折痕为 $D E$ ，则 $∠ C A D$ 的度数为（）

A、 $10 °$ B、 $20 °$ C、 $30 °$ D、 $40 °$

查看试题解析
8. 李强一家自驾车到离家 $500 k m$ 的九寨沟旅游，出发前将油箱加满油．下表记录了轿车行驶的路程 $x (k m)$ 与油箱剩余油量 $y (L)$ 之间的部分数据：
轿车行驶的路程 $x / k m$
0
100
200
300
400
…
油箱剩余油量 $y / L$
50
42
34
26
18
…
下列说法不正确的是（）

A、该车的油箱容量为 $50 L$ B、该车每行驶100km耗油8L C、油箱剩余油量 $y (L)$ 与行驶的路程 $x (k m)$ 之间的关系式为 $y = 50 - 8 x$ D、当李强一家到达九寨沟时，油箱中剩余 $10 L$ 油

查看试题解析
9. 如图，在 $△ A B C$ 中，按以下步骤作图：①分别以点B和点C为圆心，大于 $\frac{1}{2} B C$ 的长为半径作弧，两弧相交于点M和N ，连接 $M N$ ，分别与 $A B$ ， $B C$ 交于点D和E；②以点A为圆心，任意长为半径作弧，交 $A B$ 于点G ，交 $A C$ 于点H；③分别以点G和点H为圆心，大于 $\frac{1}{2} G H$ 的长为半径作弧，两弧相交于点P；④作射线 $A P$ ，分别交 $B C$ ， $M N$ 于点F ， Q ．若 $∠ B = 40 °$ ， $∠ C = 60 °$ ，则 $∠ E Q F$ 的度数为（）

A、 $10 °$ B、 $15 °$ C、 $20 °$ D、 $25 °$

查看试题解析
10. 如图，在 $△ A B C$ 中， $A B = A C$ ， $B D$ 为 $A C$ 边上的高， $B E$ 平分 $∠ A B D$ ，点F在 $B D$ 上连接 $E F$ 并延长交 $B C$ 于点G ，若 $B G = E G$ ， $∠ A = 2 ∠ D E F$ ，有下列结论：① $∠ D E F = ∠ C B D$ ；② $∠ A B E + ∠ C B D = 45 °$ ；③ $E G ⊥ B C$ ；④ $B E = B C$ ；⑤ $B F = C E$ ．其中一定成立的有（）

A、5个 B、4个 C、3个 D、2个

查看试题解析

二、填空题

11. 足球、篮球、排球“三大球”单列成为体育中考第一类项目（自主选考三选一），考生若任选一项参加考试，则考生选择考篮球的概率为．

查看试题解析
12. 若 $∠ α$ 与 $∠ β$ 是对顶角， $∠ α$ 的补角是 $120 °$ ，则 $∠ β$ 的余角的度数为．

查看试题解析
13. 已知 $4 x^{2} - x = 1013$ ，则代数式 $(2 x + 1) (4 x - 3)$ 的值为.

查看试题解析
14. 若一个等腰三角形的一条边是另一条边的k倍，我们把这样的等腰三角形叫做“k倍边等腰三角形”如果一个等腰三角形是“3倍边等腰三角形”，且周长为 $35 c m$ ，那么该等腰三角形的底边长为 $c m$ ．

查看试题解析
15. 如图， $△ A B C$ 的面积是 $150 c m^{2}$ ，最长边 $A B = 30 c m$ ， $A D$ 平分 $∠ B A C$ ，点M ， N分别是 $A D$ ， $A C$ 上的动点，则 $C M + M N$ 的最小值为 $c m$ ．

查看试题解析

三、解答题

16. 计算：

(1)、 $2 m^{3} n \cdot {(- 3 m n^{2})}^{2}$ ；

(2)、 $2^{- 2} + (2 - π)^{0} + (- 2)^{2023} \times {(- \frac{1}{2})}^{2022}$ ．

查看试题解析
17. 先化简，再求值： $[(x + 2 y) (2 y - x) - 4 y (- x + y)] \div (- 2 x)$ ，其中 $x = 1$ ， $y = 2$ ．

查看试题解析
18. 下面三个试验中我们都可以通过看图估算或者图形计算各自的概率．

(1)、在一次试验中，老师共做了400次掷图钉游戏并记录了游戏的结果，绘制了钉尖朝上的频率折线统计图，如图①所示，请估计钉尖朝上的概率；

(2)、图②是一个可以自由转动的转盘，任意转动该转盘，当转盘停止时，计算指针落在丁区域的概率；

(3)、有一个小球在图③所示的三个完全相同的正方形拼成的地板上自由滚动，求小球最终停留在黑色区域的概率．

查看试题解析
19. 如图，已知 $∠ α$ 及线段 $b$ ，求作一个三角形，使得它的两内角分别为 $α$ 和 $2 α$ ，且这两内角的夹边长为 $b$ ．（要求：尺规作图，保留作图痕迹，不写作法）

查看试题解析
20. 如图，在 $△ A B C$ 中， $A B = A C$ ， AB的垂直平分线DE分别交AC，AB于点D，E.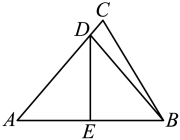

(1)、若 $∠ A = 50 °$ ，求 $∠ C$ 的度数：

(2)、若 $A B = 7$ 且 $△ C B D$ 周长为12，求BC的长.

查看试题解析
21. 如图，点E ， F分别在 $A B$ ， $C D$ 上， $A F ⊥ C E$ 于点O ， $∠ 1 = ∠ B$ ， $∠ A + ∠ 2 = 90 °$ ．试说明： $A B ∥ C D$ ．
下面是某同学的说理过程，请阅读并补全说理过程．

解：因为 $A F ⊥ C E$ ，所以 $∠ A O E = 90 °$ ．
又因为 $∠ 1 = ∠ B$ ，
根据“（  ）”，
所以     ▲   $∥$      ▲  ．
根据“（  ）”，
所以 $∠ A F B = ∠ A O E$ ．
所以 $∠ A F B =$      ▲   $°$ ．
又因为 $∠ A F C + ∠ A F B + ∠ 2 = 180 °$ ，
所以 $∠ A F C + ∠ 2 =$      ▲   $°$ ．
又因为 $∠ A + ∠ 2 = 90 °$ ，
根据“（  ）”，
所以 $∠ A = ∠ A F C$ ．
根据“（  ）”，
所以 $A B ∥ C D$ ．

查看试题解析
22. 为了迎接2023年渠县川渝龙舟赛，达州市周边的县市先组织进行了赛龙舟选拔赛．图是甲、乙两队在选拔赛时的路程y（米）与时间x（分）之间的关系图象，请你根据图象，回答下列问题：

(1)、图象中的自变量是，因变量是；

(2)、这次龙舟选拔赛的全程是米，队先到达终点；

(3)、求甲队和乙队相遇时乙队的速度；

(4)、求甲队和乙队相遇时，甲队划行了多少米．

查看试题解析
23. 如图，已知 $A B = A D$ ， $A E = A C$ ， $∠ B A C = ∠ D A E$ ，则 $∠ E$ 和 $∠ C$ 相等吗？请说明理由．

查看试题解析
24. 知识生成：我们已经知道，通过计算几何图形的面积可以表示一些代数恒等式．
例如：由图①可以得到 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ ，基于此，请解答下列问题：

(1)、直接应用：若 $x y = 5$ ， $x + y = 7$ ，直接写出 $x^{2} + y^{2}$ 的值为；

(2)、类比应用：填空：
①若 $x (4 - x) = 2$ ，则 $x^{2} + (x - 4)^{2} =$ ；
②若 $(x - 3) (x - 5) = 2$ ，则 $(x - 3)^{2} + (x - 5)^{2} =$ ；

(3)、知识迁移：如图②，一农家乐准备在原有长方形用地（即长方形 $A B C D$ ）上进行装修和扩建，先用长为120m的装饰性篱笆围起该长方形用地，再以 $A D$ ， $C D$ 为边分别向外扩建正方形 $A D G H$ 、正方形 $D C E F$ 的空地，并在这两块正方形空地上建造功能性花园，该功能性花园面积和为 $2000 m^{2}$ ，求原有长方形用地 $A B C D$ 的面积．

查看试题解析
25. 在 $△ A B C$ 中， $A B = A C$ ， $D$ 是直线 $A B$ 上一动点（不与点 $A$ ， $B$ 重合）．

(1)、如图1，若 $∠ A < 90 °$ ，点 $D$ 在边 $A B$ 上， $D E ⊥ A B$ 交 $B C$ 于点 $E$ ， $E F ⊥ B C$ 交 $A C$ 于点 $F$ ．若 $∠ A F E = 155 °$ ，求 $∠ D E F$ 的度数．

(2)、如图2，若 $∠ B A C = 90 °$ ，点 $D$ 在边 $A B$ 上， $B E ⊥ C D$ ，交直线 $C D$ 于点 $E$ ，交直线 $A C$ 于点 $F$ ．
①线段 $A B$ ， $A F$ ， $B D$ 三者之间的数量关系是 ▲ ；

②若点 $D$ 在 $A B$ 的延长线①中的结论是否成立？若成立，请给出推理过程；若不成立，请画出图形，并直接写出 $A B$ ， $A F$ ， $B D$ 三者之间的数量关系．

③若点 $D$ 在边 $A B$ 上，且 $C D = 2 B E$ ，请判断 $A B$ ， $A F$ ， $B C$ 三者之间的数量关系，并说明理由．

查看试题解析

轿车行驶的路程 $x / k m$	0	100	200	300	400	…
油箱剩余油量 $y / L$	50	42	34	26	18	…