四川省广元市朝天区2022-2023学年七年级下学期期末数学试题

试卷更新日期：2023-08-29 类型：期末考试

进入出卷网下载

一、单选题

1. 16的算术平方根是（）

A、 $\pm 4$ B、4 C、 $\sqrt{16}$ D、2

查看试题解析
2. 如图，如果要把河流中的水引到水池 $A$ 中，那么在河岸的 $B$ 处（已知 $A B ⊥ C D$ ）挖渠就能使得水渠 $A B$ 的长度最短，这样做的数学依据是（）

A、点到直线的距离 B、垂线段最短 C、两点确定一条直线 D、两点之间线段最短

查看试题解析
3. 下列各式中，是二元一次方程的是（）

A、 $4 x - 5 y = 5$ B、 $x y - y = 1$ C、 $4 x + 5 y$ D、 $\frac{2}{x} + \frac{5}{y} = \frac{1}{7}$

查看试题解析
4. 在平面直角坐标系中，点 $(2 - m ， 2 m - 1)$ 在第四象限，且到y轴的距离为3，则m的值为（）

A、 $- 1$ B、1 C、 $- 2$ D、 $- 1$ 或5

查看试题解析
5. 下面调查中，最适合采用抽样调查方式的是（）

A、调查乘坐飞机的旅客是否携带了违禁物品 B、调查一捆钞票里有没有假钞 C、调查广元市居民的人均年消费情况 D、调查用于发射卫星的运载火箭的各零部件

查看试题解析
6. 已知 $a > b$ ，下列不等式成立的是（）

A、 $a + 2 < b + 2$ B、 $a - c < b - c$ C、 $- 5 a > - 5 b$ D、 $\frac{a}{4} > \frac{b}{4}$

查看试题解析
7. 如下图，在“ $A$ ”字型图中， $A B$ 、 $A C$ 被 $D E$ 所截，则 $∠ A$ 与 $∠ 4$ 是（）

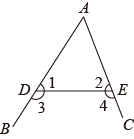A、同位角 B、内错角 C、同旁内角 D、邻补角

查看试题解析
8. 已知 ${\begin{array}{l} 2 x + 4 y = 5 \\ x - y = 10 \end{array}$ ，则 $x + y$ 的值是（　　）

A、4 B、5 C、6 D、7

查看试题解析
9. 若关于x的不等式组 ${\begin{array}{l} x < 1 ， \\ x > n - 1 \end{array}$ 恰有两个整数解，则n的取值范围是（）

A、 $- 1 ≤ n < 0$ B、 $- 1 < n \leq 0$ C、 $- 1 \leq n \leq 0$ D、 $- 1 < n < 0$

查看试题解析
10. 在平面直角坐标系中，对于点 $P (x ， y)$ ，我们把点 $P^{^{'}} (- y + 1 ， x + 1)$ 叫作点P的伴随点，已知点 $A_{1}$ 的伴随点为 $A_{2}$ ，点 $A_{2}$ 的伴随点为 $A_{3}$ ，点 $A_{3}$ 的伴随点为 $A_{4}$ ， …，这样依次得到点 $A_{2}$ ， $A_{3}$ ， …， $A_{n}$ ．若点 $A_{1}$ 的坐标为 $(2 ， 4)$ ，则点 $A_{2023}$ 的坐标为（）

A、 $(- 3 ， 3)$ B、 $(- 2 ， - 2)$ C、 $(3 ， - 1)$ D、 $(2 ， 4)$

查看试题解析

二、填空题

11. 已知整数x满足 $\sqrt{27} < x < 7$ ，则x的值为．

查看试题解析
12. 一组数据的最大值为 $169$ ，最小值为 $143$ ，在绘制频数直方图时要求组距为 $3$ ，则组数为．

查看试题解析
13. 如图，直线 $a ∥ b$ ， $R t △ A B C$ 的直角顶点C在直线b上，若 $∠ 1 = 40 °$ ，则 $∠ 2$ 的度数为．

查看试题解析
14. 方程组 ${\begin{array}{l} x + y = 3 \\ 2 (x + y) - y = 5 \end{array}$ 的解是．

查看试题解析
15. 如图，平移线段 $A B$ ，使点B到点C ，则平移后点A的坐标为．

查看试题解析
16. 已知 $m$ ， $n$ 为常数，若 $m x + n > 0$ 的解集为 $x > \frac{2}{5}$ ，则 $n x - m < 0$ 的解集是．

查看试题解析

三、解答题

17. 计算： $| \sqrt{25} - 3 | + \sqrt[3]{- 27} - (- 2)^{3}$ ．

查看试题解析
18. 解不等式组： ${\begin{array}{l} 3 x + 5 > - 1 ， \\ \frac{9 x + 1}{4} \leq x + 4 ， \end{array}$ 并把解集在数轴上表示出来．

查看试题解析
19. 如图，在平面直角坐标系中，三角形 $A B C$ 的顶点都在网格点上，其中点C的坐标为 $(1 ， 2)$ ．

(1)、点A的坐标是点B的坐标是．

(2)、画出将三角形 $A B C$ 先向左平移2个单位长度，再向上平移1个单位长度所得到的三角形 $A^{'} B^{'} C^{'}$ ．请写出三角形 $A^{'} B^{'} C^{'}$ 的三个顶点坐标；

(3)、求三角形 $A B C$ 的面积．

查看试题解析
20. 如图， $A B ∥ D G$ ， $∠ 1 + ∠ 2 = 180 °$ ，

(1)、求证： $A D ∥ E F$ ；

(2)、若 $D G$ 是 $∠ A D C$ 的平分线， $∠ 2 = 148 °$ ，求 $∠ E F D$ 的度数．

查看试题解析
21. 为了解某地区中学生创新能力大赛的比赛情况，随机调查了部分参赛同学的成绩x（百分制），整理并绘制成如下统计图表（不完整）．
分数段
频数
频率
          $60 \leq x < 70$
a
0.1
          $70 \leq x < 80$
90
b
          $80 \leq x < 90$
c
0.4
          $90 \leq x \leq 100$
60
0.2

请根据图表中提供的信息，解答下列问题：

(1)、统计表中： $a =$ ， $b =$ ， $c =$ ；

(2)、补全频数分布直方图；

(3)、若将调查的该地区参赛同学的成绩绘制成扇形统计图，且比赛成绩达到80分为优秀，求比赛成绩为优秀的学生所在扇形对应的圆心角度数．

查看试题解析
22. 位于广元市朝天区的朝天古城有着悠久的历史，距今已有2000多年，因其独特的民俗文化，吸引了众多游客前来观光．为了抓住商机，某商店决定购进A ， B两种纪念品，已知购进A种纪念品10件，B种纪念品5件，共需要2000元；购进A种纪念品5件，B种纪念品3件，共需要1050元．

(1)、购进A ， B两种纪念品每件各需要多少元？

(2)、若该商店决定拿出4000元全部用来购进这两种纪念品，其中每种纪念品至少购进12件，那么该商店共有几种进货方案？

查看试题解析
23. 阅读下面的材料：
对于实数a ， b ，我们定义符号 $m i n {a ， b}$ 的意义为：当 $a \geq b$ 时， $m i n {a ， b} = b$ ，如： $m i n {4 ， - 2} = - 2$ ， $m i n {5 ， 5} = 5$ ．
根据上面的材料回答下列问题：

(1)、 $m i n {- \sqrt{3} ， - 2} =$ ；

(2)、当 $m i n {\frac{2 x - 3}{2} ， \frac{x + 2}{3}} = \frac{x + 2}{3}$ 时，求x的取值范围．

查看试题解析
24. 已知 $x - 1$ 的平方根是 $\pm 2$ ， $4 x + y$ 的立方根是 $3$ ， $y - x$ 的算术平方根是 $m$ ．

(1)、求 $m$ 的值；

(2)、如果 $5 + m = a + b$ ，其中 $a$ 是整数，且 $0 < b < 1$ ，求 $a - {(\sqrt{2} - b)}^{2}$

查看试题解析
25. 已知当m ， n都是实数，且满足 $2 m = 4 + n$ 时，称点 $P (m - 1 ， \frac{n + 2}{2})$ 为“如意点”．

(1)、当 $m = 2$ 时，写出“如意点”：；

(2)、判断点 $A (3 ， 3)$ 是否为“如意点”，并说明理由；

(3)、若点 $M (a ， 2 a - 1)$ 是“如意点”，请判断点M在第几象限，并说明理由．

查看试题解析
26. 已知直线 $A B ∥ C D$ ，点E ， F分别在 $A B ， C D$ 上，O是平面内一点(不在直线 $A B$ 、 $C D$ 、 $E F$ 上)， $O G$ 平分 $∠ E O F$ ，射线 $O H ∥ A B$ ，交 $E F$ 于点H ．

(1)、如图①，若 $∠ A E O = 45 ° ， ∠ C F O = 75 °$ ，则 $∠ H O G =$ ，

(2)、如图②，若 $∠ A E O = 150 ° ， ∠ H O G = 20 °$ ，则 $∠ C F O =$ ；

(3)、直接写出点O在不同位置时 $∠ A E O$ 、 $∠ C F O$ 和 $∠ H O G$ 三个角之间满足的数量关系．

查看试题解析

分数段	频数	频率
$60 \leq x < 70$	a	0.1
$70 \leq x < 80$	90	b
$80 \leq x < 90$	c	0.4
$90 \leq x \leq 100$	60	0.2