四川省广安市岳池县2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-08-29 类型:期末考试
一、单选题
-
1. 的立方根是( )A、2 B、 C、 D、42. 在平面直角坐标系中,点在第二象限,则的值可能为( )A、1 B、0 C、 D、3. 在如图所示的字母“”中,和的位置关系是( )
 A、互为邻补角 B、互为内错角 C、互为同位角 D、互为同旁内角4. 为了获取关于人口全面正确的信息,我国每年对人口进行一次全面调查,每年会进行一次人口变动情况抽样调查.下列调查某省人口变动情况选取的样本中,合适的是( )A、对全省居民进行调查 B、对该省某市的居民进行调查 C、对该省某社区居民进行调查 D、随机选取该省的居民进行调查5. 一款西服上标有下列信息:
A、互为邻补角 B、互为内错角 C、互为同位角 D、互为同旁内角4. 为了获取关于人口全面正确的信息,我国每年对人口进行一次全面调查,每年会进行一次人口变动情况抽样调查.下列调查某省人口变动情况选取的样本中,合适的是( )A、对全省居民进行调查 B、对该省某市的居民进行调查 C、对该省某社区居民进行调查 D、随机选取该省的居民进行调查5. 一款西服上标有下列信息:洗涤说明
以下网袋机洗,不可漂白,低温熨烫,不可干洗,不可曝晒,请勿浸泡
根据信息,关于这款西服的洗涤温度范围,在数轴上表示正确的是( )
A、 B、
B、 C、
C、 D、
D、 6. 如图,三角形沿射线方向平移得到三角形 . 若 , 则( )
6. 如图,三角形沿射线方向平移得到三角形 . 若 , 则( )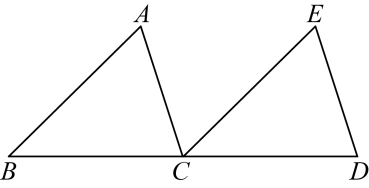 A、 B、 C、 D、无法确定7. 如图,已知直线 , , 直角三角板的直角顶点落在直线上.若 , 则的度数为( )
A、 B、 C、 D、无法确定7. 如图,已知直线 , , 直角三角板的直角顶点落在直线上.若 , 则的度数为( ) A、 B、 C、 D、8. 某种仪器由1个部件和2个部件配套构成,每名工人每天可以加工50个部件或60个部件,现有72名工人,应怎样安排人力,才能使每天加工的部件和部件配套?设安排名工人加工部件,安排y名工人加工部件,则可列出方程组( )A、 B、 C、 D、9. 下列命题是真命题的是( )A、若 , 则 B、相等的两个角互为对顶角 C、正实数一定有两个平方根 D、过一点有且只有一条直线与已知直线平行10. 若关于x , y的二元一次方程组的解满足 , 则k的值为( )A、0 B、1 C、2 D、-1
A、 B、 C、 D、8. 某种仪器由1个部件和2个部件配套构成,每名工人每天可以加工50个部件或60个部件,现有72名工人,应怎样安排人力,才能使每天加工的部件和部件配套?设安排名工人加工部件,安排y名工人加工部件,则可列出方程组( )A、 B、 C、 D、9. 下列命题是真命题的是( )A、若 , 则 B、相等的两个角互为对顶角 C、正实数一定有两个平方根 D、过一点有且只有一条直线与已知直线平行10. 若关于x , y的二元一次方程组的解满足 , 则k的值为( )A、0 B、1 C、2 D、-1二、填空题
-
11. 如图所示,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是 .
 12. 用代入消元法解方程组时,消去 , 得到关于的方程是 . (不用化简)13. 若关于的不等式的解集是 , 则的取值范围是 .14. 如图是某局象棋比赛的残局(部分图),在残局上建立平面直角坐标系,若“
12. 用代入消元法解方程组时,消去 , 得到关于的方程是 . (不用化简)13. 若关于的不等式的解集是 , 则的取值范围是 .14. 如图是某局象棋比赛的残局(部分图),在残局上建立平面直角坐标系,若“ ”和“
”和“ ”的坐标分别是和 , 则“
”的坐标分别是和 , 则“ ”的坐标为 .
”的坐标为 .
 15. 已知正方形的面积为5,点在数轴上,且表示的数为1,现以为圆心,为半径画圆,和数轴交于点 , 如图所示,则点表示的数为 .
15. 已知正方形的面积为5,点在数轴上,且表示的数为1,现以为圆心,为半径画圆,和数轴交于点 , 如图所示,则点表示的数为 .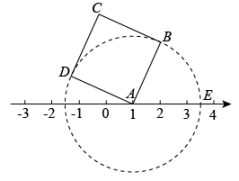 16. 第一象限内有两点 , 将线段平移使点P、Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是 .
16. 第一象限内有两点 , 将线段平移使点P、Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是 .三、解答题
-
17. 解方程组:18.(1)、计算:;(2)、解不等式组:19. 在如图所示的平面直角坐标系中,三角形的顶点均在格点上.
 (1)、点到轴的距离是 , 点的坐标是;(2)、画出将三角形向右平移个单位长度、向下平移个单位长度后得到的三角形 .20. 如图,已知于点 , , . 求证: .
(1)、点到轴的距离是 , 点的坐标是;(2)、画出将三角形向右平移个单位长度、向下平移个单位长度后得到的三角形 .20. 如图,已知于点 , , . 求证: .
完成下面的证明过程.
证明:∵(已知),
∴( ).
∵(已知),
∴ ,
∴( ),
∴ ▲ (两直线平行,同旁内角互补).
∵(已知),
∴ ▲ ( ),
∴( ).
21. 如图,某小区计划开发一块长32m、宽21m的长方形空地,在这块空地上修建一个长是宽的1.6倍,面积为的篮球场.若比赛用的篮球场要求长在25m到30m之间,宽在13m到20m之间,修建的这个篮球场符合比赛要求吗?请说明理由.(参考数据: , )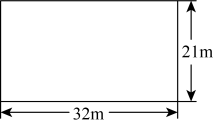 22. 每年的月日为“国家安全教育日”.某中学在年安全教育日组织全校学生参加了“中学生安全知识”竞赛,将学生的成绩(百分制)分为四个等级::;:;:;: . 该校数学兴趣小组从中随机抽取部分同学的竞赛成绩并绘制成如下不完整的统计图.
22. 每年的月日为“国家安全教育日”.某中学在年安全教育日组织全校学生参加了“中学生安全知识”竞赛,将学生的成绩(百分制)分为四个等级::;:;:;: . 该校数学兴趣小组从中随机抽取部分同学的竞赛成绩并绘制成如下不完整的统计图.
请根据以上统计图,完成下面的问题:
(1)、抽取的学生总人数是人;补全频数分布直方图;(2)、扇形统计图中,;求等级对应的扇形圆心角的度数 .23. 如图1是十二星座中的天秤座的主要星系连线图,将各个主要星系分别用字母表示,得到如图2的几何示意图,已知 . 试说明 .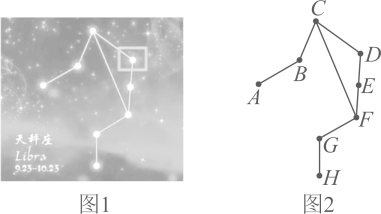 24. 武胜脐橙和邻水脐橙是农业部划定的长江上中游柑橘产业带之二,也是广安市的特色水果.某超市专门销售这两种特色脐橙.已知购进武胜脐橙和邻水脐橙需要元;购进武胜脐橙和邻水脐橙需要元.(1)、购进每千克武胜脐橙和邻水脐橙分别需要多少钱?(2)、若该超市决定每天购进这两种特色脐橙共 , 且购买资金不少于元又不多于元,设每天购进武胜脐橙(x为正整数),则该超市有哪几种购买方案?25. 【阅读】定义:使方程(组)与不等式(组)同时成立的未知数的值称为此方程(组)和不等式(组)的“理想解”.例如:已知方程与不等式 , 当时, , 同时成立,则称是方程与不等式的“理想解”.
24. 武胜脐橙和邻水脐橙是农业部划定的长江上中游柑橘产业带之二,也是广安市的特色水果.某超市专门销售这两种特色脐橙.已知购进武胜脐橙和邻水脐橙需要元;购进武胜脐橙和邻水脐橙需要元.(1)、购进每千克武胜脐橙和邻水脐橙分别需要多少钱?(2)、若该超市决定每天购进这两种特色脐橙共 , 且购买资金不少于元又不多于元,设每天购进武胜脐橙(x为正整数),则该超市有哪几种购买方案?25. 【阅读】定义:使方程(组)与不等式(组)同时成立的未知数的值称为此方程(组)和不等式(组)的“理想解”.例如:已知方程与不等式 , 当时, , 同时成立,则称是方程与不等式的“理想解”.根据以上信息,解决下列问题:
(1)、是方程与下列不等式(组)的“理想解”;(填序号)①;②;③
(2)、若是方程组与不等式的“理想解”,求的取值范围.26. 如图,直线 , 直线与 , 分别交于点 , . 小安将直角三角板( , )按如图1放置,使点分别在直线上,且 . (1)、填空:(填“”“”或“=”).(2)、如图2,的平分线交直线于点 .
(1)、填空:(填“”“”或“=”).(2)、如图2,的平分线交直线于点 .①当时,求的度数;
②小安将三角板沿直线左右移动,保持 , 点分别在直线和直线上移动,请直接写出的度数(用含的式子表示).