四川省内江市2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-08-29 类型：期末考试

进入出卷网下载

一、单选题

1. 若关于x的方程 $2 x^{m - 1} + 3 = 0$ 是一元一次方程，则m的值为（）

A、－1 B、0 C、1 D、2

查看试题解析
2. 下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（）

A、赵爽弦图 B、笛卡尔心形线 C、科克曲线 D、斐波那契螺旋线

查看试题解析
3. 已知 $a < b$ ，下列式子不成立的是（）

A、 $a + c < b + c$ B、 $a - 2 < b - 2$ C、 $2 a < 2 b$ D、 $- 3 a < - 3 b$

查看试题解析
4. 如图，已知 $∠ 1 + ∠ 2 + ∠ 3 = 240 °$ ，那么 $∠ 4$ 的度数为（）

A、 $60 °$ B、 $90 °$ C、 $110 °$ D、 $120 °$

查看试题解析
5. 关于x、y的二元一次方程组 ${\begin{array}{l} 2 x + y = 3 a \\ x - 2 y = 9 a \end{array}$ 的解是二元一次方程 $x + 3 y = 24$ 的一个解，则a的值是（）

A、 $- 4$ B、 $- 2$ C、2 D、4

查看试题解析
6. 只用下列正多边形地砖中的一种，能够铺满地面的是（）

A、正五边形 B、正六边形 C、正八边形 D、正十边形

查看试题解析
7. 如图， $△ A D E$ 与 $△ C D B$ 关于点D成中心对称，连接AB ，以下结论错误的是（）

A、 $A D = C D$ B、 $∠ C = ∠ E$ C、 $A E = C B$ D、 $S_{△ A D E} = S_{△ A D B}$

查看试题解析
8. 李老师准备用30元钱全部购买A，B两种型号的签字笔（两种型号的签字笔都买），A型签字笔每支5元，B型签字笔每支2元，则李老师的购买方案有（）

A、4种 B、3种 C、2种 D、1种

查看试题解析
9. 如图，两个直角三角形重叠在一起，将其中一个沿点B到点C的方向平移到 $△ D E F$ 的位置， $A B = 10$ ， $D H = 4$ ， $B C = 15$ ，平移距离为6，则阴影部分的面积为（）

A、40 B、42 C、45 D、48

查看试题解析
10. 阅读解方程的途径：

按照图1所示的途径，已知关于x的方程 $\frac{a | x |}{2} + c = \frac{b | x + 1 |}{3}$ 的解是 $x = 1$ 或 $x = 2$ （a、b、c均为常数），则关于x的方程 $\frac{a | k x + m |}{2} + c = \frac{b | k x + m + 1 |}{3}$ （k、m为常数， $k \neq 0$ ）的解为（）

A、 $x_{1} = 1 ， x_{2} = 2$ B、 $x_{1} = \frac{1 - m}{k} ， x_{2} = \frac{2 - m}{k}$ C、 $x_{1} = \frac{1 + m}{k} ， x_{2} = \frac{2 + m}{k}$ D、 $x_{1} = 1 + k + m ， x_{2} = 2 + k + m .$

查看试题解析
11. 若关于 $x$ 的一元一次不等式组 ${\begin{cases} 2 (x + 1) < x + 3 \\ x - a \leq a + 5 \end{cases}$ 的解集是 $x < 1$ ，且 $a$ 为非正整数，则满足条件的 $a$ 的取值有（）个.

A、1 B、2 C、3 D、4

查看试题解析
12. 如图，已知 $∠ A O B$ 的大小为 $α$ ， $P$ 是 $∠ A O B$ 内部的一个定点，且 $O P = 5$ ，点 $E$ 、 $F$ 分别是 $O A$ 、 $O B$ 上的动点，若 $△ P E F$ 周长的最小值等于 $5$ ，则 $α =$ （）

A、 $30 °$ B、 $45 °$ C、 $60 °$ D、 $90 °$

查看试题解析

二、填空题

13. 已知方程 $3 x - y = 9$ ，则用含x的代数式表示y为．

查看试题解析
14. 已知 $△ A B C$ 是等腰三角形，如果它的两条边的长分别为 $8 c m$ 和 $3 c m$ ，则它的周长为
$c m$ ．

查看试题解析
15. 如图，六边形ABCDEF内部有一点G，连结BG、DG. 若 $∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 + ∠ 5 = 440 °$ ，则∠BGD的大小为度.

查看试题解析
16. 若 $6 x = 3 y + 12 = 2 z$ ，且 $y \geq 0$ ， $z \leq 9$ ，设 $m = 2 x + y - 3 z$ ，则m的取值范围为．

查看试题解析

三、解答题

17.

(1)、解方程： $\frac{4 x - 1}{6} = 1 - \frac{3 x - 1}{3}$ ．

(2)、解不等式组 ${\begin{array}{l} 2 - x \leq 2 (x + 4) \\ x < \frac{x - 1}{3} + 1 \end{array}$ ，并把它们的解集表示在数轴上．

查看试题解析
18. 如图，在正方形网格中，点A、B、C均在格点上．

⑴画出 $△ A_{1} B_{1} C_{1}$ ，使 $△ A_{1} B_{1} C_{1}$ 和 $△ A B C$ 关于直线l成轴对称；
⑵把 $△ A B C$ 绕C点顺时针旋转 $90 °$ ，在网格中画出旋转后得到的 $△ A_{2} B_{2} C$ ；
⑶在直线l上画出点P ，使得 $P A + P B$ 最小．

查看试题解析
19. 我国航天事业的飞速发展引发了航空航天纪念品的热销，某商店准备购进甲、乙两类关于航空航天的纪念品进行销售.已知甲类纪念品的进价为m元/件，乙类纪念品的进价比甲类的进价多5元/件.若每件甲类纪念品的售价是在其进价的基础上提高了 $60 ％$ ，每件乙类纪念品的售价是在其进价的基础上提高了 $40 ％$ ，根据上述条件，回答下面问题：

(1)、请用含有m的代数式填写下表：

进价/元
售价/元
甲类纪念品
m
乙类纪念品

(2)、该商店分别购进甲类纪念品100件，乙类纪念品80件.两类纪念品全部售出后所得的总利润为1080元，问每件甲、乙两类纪念品进价分别多少元？

查看试题解析
20. 如图，BD平分∠ABC．∠ABD=∠ADB．

(1)、求证：AD∥BC；

(2)、若BD⊥CD，∠BAD=α，求∠DCB的度数（用含α的代数式表示）．

查看试题解析
21. 文教店用1200元购进了甲、乙两种纪念册，已知甲种纪念册进价为每本12元，乙种纪念册进价为每本10元，文教店在销售时甲种纪念册售价为每本15元，乙种纪念册售价为每本12元，全部售完后共获利270元

(1)、求文教店购进甲、乙两种纪念册各多少本？

(2)、若文教店以原进价再次购进甲、乙两种纪念册，且购进甲种纪念册的数量不变，而购进乙种纪念册的数量是第一次的2倍，乙种纪念册按原售价销售，而甲种纪念册降价销售，当两种纪念册销售完毕时，要使再次购进的纪念册获利不少于340元，求甲种纪念册每本最低售价应为多少元？

查看试题解析
22. 利用图形这一直观性语言，在一定程度上可以降低我们认识和理解抽象逻辑推理的难度；利用图形建构几何直观，可以轻松实现空间形式和数量关系的相互转化．让我们在如下的问题解决中体验一下吧！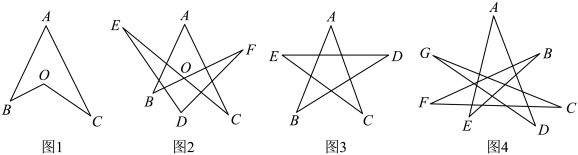

(1)、【模块探究】
如图1，求证： $∠ B O C = ∠ A + ∠ B + ∠ C$

(2)、【直观应用】
①应用上述结论，若图2中， $∠ E O F = α$ ，则 $∠ A$ 、 $∠ B$ 、 $∠ C$ 、 $∠ D$ 、 $∠ E$ 、 $∠ F$ 的度数之和等于 ▲ ．（直接给出结论，不必说明理由）
②应用上述结论，求图3所示的五角星中， $∠ A$ 、 $∠ B$ 、 $∠ C$ 、 $∠ D$ 、 $∠ E$ 的度数之和是多少？并证明你的结论．

(3)、【类比联系】
如图4，求 $∠ A$ 、 $∠ B$ 、 $∠ C$ 、 $∠ D$ 、 $∠ E$ 、 $∠ F$ 、 $∠ G$ 的度数之和是多少？并证明你的结论．

查看试题解析

	进价/元	售价/元
甲类纪念品	m
乙类纪念品