四川省遂宁市2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-08-29 类型:期末考试
一、单选题
-
1. 若的值比的值小 , 则的值为( )A、 B、 C、 D、2. 下列表示我国古代窗棂样式结构图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 若 , 则下列不等式正确的是( )A、 B、 C、 D、4. 某中学七年级二班学生源源家和依依家到学校的直线距离分别是5km和3km.那么源源,依依两家的直线距离不可能是( )A、8km B、4 km C、2km D、1km5. 如果且 , 那么的值是( )A、5 B、10 C、 D、6. 若正多边形的一个外角是 , 则该正多边形的内角和为( )A、 B、 C、 D、7. 能够铺满地面的正多边形组合是( )A、正六边形和正五边形 B、正方形和正八边形 C、正五边形和正八边形 D、正三角形和正八边形8. 如图, , 且点在上,点在同一直线上,若则的长为( )
3. 若 , 则下列不等式正确的是( )A、 B、 C、 D、4. 某中学七年级二班学生源源家和依依家到学校的直线距离分别是5km和3km.那么源源,依依两家的直线距离不可能是( )A、8km B、4 km C、2km D、1km5. 如果且 , 那么的值是( )A、5 B、10 C、 D、6. 若正多边形的一个外角是 , 则该正多边形的内角和为( )A、 B、 C、 D、7. 能够铺满地面的正多边形组合是( )A、正六边形和正五边形 B、正方形和正八边形 C、正五边形和正八边形 D、正三角形和正八边形8. 如图, , 且点在上,点在同一直线上,若则的长为( ) A、9 B、6 C、3 D、29. 若方程与关于的方程的解相同,则的值为( )A、1 B、 C、 D、10. 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术,其中方程术是其最高的代数成就.《九章算术》中有这样一个问题:“今有善行者行一百步,不善行者行六十步.今不善行者先行一百步,善行者追之,问几何步及之?”译文:“相同时间内,走路快的人走100步,走路慢的人只走60步.若走路慢的人先走100步,走路快的人要走多少步才能追上?(注:步为长度单位)”设走路快的人要走x步才能追上,根据题意可列出的方程是( )A、 B、 C、 D、11. 定义一种新运算: . 例如: , 那么不等式的正整数解是( )A、 B、1 C、0和1 D、212. 如图,已知三角形的面积为 , . 现将三角形沿直线向右平移m个单位得到三角形 . 当三角形扫过的面积为时,m的值是( )
A、9 B、6 C、3 D、29. 若方程与关于的方程的解相同,则的值为( )A、1 B、 C、 D、10. 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术,其中方程术是其最高的代数成就.《九章算术》中有这样一个问题:“今有善行者行一百步,不善行者行六十步.今不善行者先行一百步,善行者追之,问几何步及之?”译文:“相同时间内,走路快的人走100步,走路慢的人只走60步.若走路慢的人先走100步,走路快的人要走多少步才能追上?(注:步为长度单位)”设走路快的人要走x步才能追上,根据题意可列出的方程是( )A、 B、 C、 D、11. 定义一种新运算: . 例如: , 那么不等式的正整数解是( )A、 B、1 C、0和1 D、212. 如图,已知三角形的面积为 , . 现将三角形沿直线向右平移m个单位得到三角形 . 当三角形扫过的面积为时,m的值是( ) A、3 B、4 C、5 D、613. 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,∠BAC的度数为( )
A、3 B、4 C、5 D、613. 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,∠BAC的度数为( )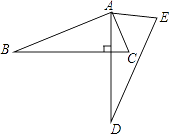 A、60° B、75° C、85° D、90°14. 已知关于的不等式组的整数解共有5个,则的取值范围是( )A、 B、 C、 D、15. 如图,为的中线,为的中线,为的中线……按此规律,为的中线.若的面积为S,则的面积为( )
A、60° B、75° C、85° D、90°14. 已知关于的不等式组的整数解共有5个,则的取值范围是( )A、 B、 C、 D、15. 如图,为的中线,为的中线,为的中线……按此规律,为的中线.若的面积为S,则的面积为( )
 A、 B、 C、 D、16. 如图,、分别是的高和角平分线,点是延长线上一点,交于点 , 交于点 , 交于点 . 有如下结论:①;②;③;④ . 其中正确的是( )
A、 B、 C、 D、16. 如图,、分别是的高和角平分线,点是延长线上一点,交于点 , 交于点 , 交于点 . 有如下结论:①;②;③;④ . 其中正确的是( ) A、②③ B、①②④ C、①②③④ D、①③④
A、②③ B、①②④ C、①②③④ D、①③④二、填空题
-
17. 若是一元一次方程,则 .18. 一位交警在执勤过程中,从汽车的后视镜中看见某车牌的后5位号码是
 , 该车牌的后5位号码实际是
, 该车牌的后5位号码实际是 三、解答题
-
19. 在中,为边BC上的高, , , 求:的度数.
四、填空题
-
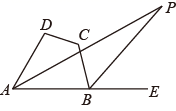
20. 如图,在四边形ABCD中, 的角平分线与 的外角平分线相交于点P,且 ,则 .
 21. 塑料凳子轻便实用,在生活中随处可见.如图,若4个塑料凳子叠放在一起的高度为60cm,6个塑料凳子叠放在一起的高度为70cm.当有11个塑料凳子整齐的叠放在一起时,其高度是cm.
21. 塑料凳子轻便实用,在生活中随处可见.如图,若4个塑料凳子叠放在一起的高度为60cm,6个塑料凳子叠放在一起的高度为70cm.当有11个塑料凳子整齐的叠放在一起时,其高度是cm.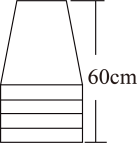 22. 按下面的程序计算,若输入x=100,输出结果是501,若输入x=25,输出结果是631,若开始输入的x值为正整数,最后输出的结果为556,则开始输入的x值 .
22. 按下面的程序计算,若输入x=100,输出结果是501,若输入x=25,输出结果是631,若开始输入的x值为正整数,最后输出的结果为556,则开始输入的x值 .

五、解答题
-
23. 解方程: .24. 解下列方程组:(1)、(2)、25. 解不等式组 , 并将解集在数轴上表示出来.
 26. 关于 , 的二元一次方程组 .(1)、若方程组的解也是二元一次方程的解,求的值;(2)、若方程组的解满足 , 求的取值范围,并写出的最大负整数解.27. 图①、图②均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A、B、C均为格点.分别在给定的网格中按下列要求作图,并保留必要的画图痕迹.
26. 关于 , 的二元一次方程组 .(1)、若方程组的解也是二元一次方程的解,求的值;(2)、若方程组的解满足 , 求的取值范围,并写出的最大负整数解.27. 图①、图②均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A、B、C均为格点.分别在给定的网格中按下列要求作图,并保留必要的画图痕迹. (1)、在图①中画出关于直线对称的图形 .(2)、在图②中画出关于点成中心对称的图形 .28. 如图,直线 , 两个三角形如图①放置,其中 , , , , 点E在直线上,点B , C均在直线上,且平分 .
(1)、在图①中画出关于直线对称的图形 .(2)、在图②中画出关于点成中心对称的图形 .28. 如图,直线 , 两个三角形如图①放置,其中 , , , , 点E在直线上,点B , C均在直线上,且平分 . (1)、求的度数;(2)、如图②,若将绕B点以每秒的速度按逆时针方向旋转(的对应点分别为).设旋转时间为t秒,当时 , 边与有何位置关系?请说明理由29. 四季莫负春光日,人生不负少年时!为了体验成长,收获快乐,学校计划组织1000名师生开展以“欢乐嘉年华,挑战致青春”为主题的研学活动.租车公司有A、B两种型号的客车可以租用,已知1辆A型车和1辆B型车可以载乘客75人,3辆A型车和2辆B型车可以载乘客180人.(1)、求一辆A型车和一辆B型车分别可以载多少乘客?(2)、若一辆A型车的租金为320元,一辆B型车的租金为400元.学校计划一共租A、B两种型号的客车25辆,在保证将全部师生送达目的地的前提下租车费用不超过9550元,学校可以选择几种租车方案?最少租车费用是多少?30. 如图,已知:点分别在的边上,连接与交于点 , .
(1)、求的度数;(2)、如图②,若将绕B点以每秒的速度按逆时针方向旋转(的对应点分别为).设旋转时间为t秒,当时 , 边与有何位置关系?请说明理由29. 四季莫负春光日,人生不负少年时!为了体验成长,收获快乐,学校计划组织1000名师生开展以“欢乐嘉年华,挑战致青春”为主题的研学活动.租车公司有A、B两种型号的客车可以租用,已知1辆A型车和1辆B型车可以载乘客75人,3辆A型车和2辆B型车可以载乘客180人.(1)、求一辆A型车和一辆B型车分别可以载多少乘客?(2)、若一辆A型车的租金为320元,一辆B型车的租金为400元.学校计划一共租A、B两种型号的客车25辆,在保证将全部师生送达目的地的前提下租车费用不超过9550元,学校可以选择几种租车方案?最少租车费用是多少?30. 如图,已知:点分别在的边上,连接与交于点 , . (1)、如图1,当都是的角平分线时,求的度数;(2)、如图2,当都是的高时,求的度数;(3)、如图3,当时,探究与的数量关系,并说明理由.
(1)、如图1,当都是的角平分线时,求的度数;(2)、如图2,当都是的高时,求的度数;(3)、如图3,当时,探究与的数量关系,并说明理由.
-