安徽省安庆市岳西县2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-29 类型：期末考试

进入出卷网下载

一、单选题

1. 若代数式 $\sqrt{8 - 2 x}$ 有意义，则实数x的取值范围是（）

A、 $x \leq - 4$ B、 $x \leq 4$ C、 $x \geq 4$ D、 $x \geq - 4$

查看试题解析
2. 下列二次根式中是最简二次根式的是（）

A、 $\sqrt{6}$ B、 $\sqrt{\frac{2}{5}}$ C、 $\sqrt{27}$ D、 $\sqrt{1.3}$

查看试题解析
3. 方程x² = 2x的解是（）.

A、 $x = 2$ B、 $x = 0$ C、 $x_{1} = 2$ ， $x_{2} = 0$ D、 $x_{1} = - 2$ ， $x_{2} = 0$

查看试题解析
4. 若关于 $x$ 的方程 $x^{2} - 2 x + k - 1 = 0$ 有实数根，则 $k$ 的取值不可以是（）

A、0 B、1 C、2 D、3

查看试题解析
5. 某公司今年4月的营业额为2500万元，按计划第二季度的总营业额要达到9100万元，设该公司5、6两月的营业额的月平均增长率为x．根据题意列方程，则下列方程正确的是（）

A、 $2500 {(1 + x)}^{2} ＝ 9100$ B、 $2500 {(1 + x %)}^{2} ＝ 9100$ C、 $2500 (1 + x) + 2500 {(1 + x)}^{2} ＝ 9100$ D、 $2500 + 2500 (1 + x) + 2500 {(1 + x)}^{2} ＝ 9100$

查看试题解析
6. 下面几组数能作为直角三角形三边长的是（）

A、2，4，5 B、5，12，13 C、12，18，22 D、4，5，8

查看试题解析
7. 已知直角三角形的周长为24，斜边长为10，则三角形的面积为（　　）

A、12 B、24 C、36 D、48

查看试题解析
8. 一个多边形的内角和是外角和的2倍，这个多边形的边数为（　　）

A、5 B、6 C、7 D、8

查看试题解析
9. 某班七个兴趣小组人数分别为4，4，5，5，x，6，7，已知这组数据的平均数是5，则这组数据的中位数和众数分别是（）

A、5，5 B、5，4 C、4，4 D、4，5

查看试题解析
10. 如图，在正方形 $A B C D$ 中，点 $E 、 F$ 分别在边 $A D$ 和 $C D$ 上， $A F ⊥ B E$ ，垂足为G，若 $\frac{A E}{E D} = 2$ ，则 $\frac{A G}{G F}$ 的值为（）

A、 $\frac{4}{5}$ B、 $\frac{5}{6}$ C、 $\frac{6}{7}$ D、 $\frac{7}{8}$

查看试题解析

二、填空题

11. 在平行四边形ABCD中，若∠A：∠B=2：3，则∠C= ．

查看试题解析
12. 计算： $\sqrt{48} - \sqrt{12} =$ ．

查看试题解析
13. 若关于 $x$ 的一元二次方程 $a x^{2} + 4 x = x^{2} + 2$ 有实数根，则 $a$ 的取值范围为．

查看试题解析
14. 新园小区计划在一块长为40米，宽为26米的矩形场地上修建三条同样宽的甬路（两条纵向、一条横向，且横向、纵向互相垂直），其余部分种花草．若要使种花草的面积达到800m² ，则甬路宽为多少米？设甬路宽为x米，则根据题意，可列方程为．

查看试题解析
15. 若一菱形的两条对角线为 $3 c m ， 4 c m$ ，则这个菱形的周长是cm．

查看试题解析
16. 如图，在平行四边形 $A B C D$ 中， $A B = 10 ， A D = 16 ， ∠ A = 60 ° ， P$ 为AD的中点，F是边AB上不与点 $A ， B$ 重合的一个动点，将 $△ A P F$ 沿 $P F$ 折叠，得到 $△ A' P F ，$ 连接 $B A' ，$ 则 $△ B A' F$ 周长的最小值为.

查看试题解析

三、解答题

17. 解方程： $x^{2} + 4 x - 4 = 0$

查看试题解析
18. $\sqrt{24} \div \sqrt{3} - \sqrt{6} \times 2 \sqrt{3}$ ．

查看试题解析
19. 在某段公路的正上方有一摄像头A距离地面7米，一天李叔叔驾驶的汽车正沿公路笔直匀速驶来，当行驶到B点时第一次摄像，此时AB两点相距25米，1.5秒后第二次摄像汽车恰好行驶到A点正下方C点，已知该路段限速60km/h，请判断李叔叔是否超速，说明理由．

查看试题解析
20. 某国产著名品牌衬衫标价为400元/件，去年中秋节和国庆节期间经过两次优惠降价为324元 /件，并且两次降价的百分率相同：

(1)、求该种衬衫每次降价的百分率；

(2)、若该种品牌衬衫的进价为300元/件，两次降价共售出此种品牌衬衫100件，为使两次降价销售的总利润不少于3120元，第一次降价至少要销售出多少件该种衬衫？

查看试题解析
21. 中华文明，源远流长，中华汉字，寓意深广，希望中学举行了“汉字听写”大赛，学校组委会随机抽取了其中的200名学生成绩（成绩 $x$ 取整数，总分100分）作为样本进行整理，得到下列统计图表（统计表遭到墨汁污染，统计图不完整）：

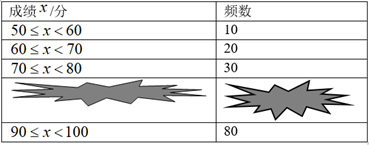
请根据所给信息，解答下列问题：

(1)、统计表中的墨汁污染的一行依次填：、；

(2)、请将频数分布直方图补充完整；

(3)、已知希望中学共有1500名学生参赛，如果规定成绩在90分以上（包括90分）的为“优秀”等次，那么该校参加这次比赛的学生中成绩为“优秀”等次的约有多少人？

查看试题解析
22. 如图，在△ABC中，AB=AC，AE是∠BAC的角平分线，点O为AB的中点，延长EO交△ABC的外角平分线于点F．

(1)、求证：EO=OF；

(2)、连接BF，试判断四边形AEBF的形状，并证明你的结论．

查看试题解析
23. 如图，在正方形 $A B C D$ 中， $A B = 5$ ， $P$ 是 $B C$ 边上任意一点， $E$ 是 $B C$ 延长线上一点，连接 $A P$ ，作 $P F ⊥ A P$ ，使 $P F = P A$ ，过点 $F$ 作 $F H ⊥ B E$ 于点 $H$ ，连接 $C F$ ， $A F$ ， $A F$ 交 $C D$ 边于点 $G$ ，连接 $P G$ ．

(1)、求证： $△ B A P ≌ △ H P F$ ；

(2)、证明： $∠ G C F = ∠ F C E$ ．

(3)、判断线段 $P G$ ， $P B$ 与 $D G$ 之间的数量关系，并证明你的结论．

查看试题解析