安徽省合肥市庐江县2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-29 类型:期末考试
一、单选题
-
1. 若代数式 在实数范围内有意义,则 的取值范围是A、x<1 B、x≤1 C、x>1 D、x≥12. 下列几组数据中能作为直角三角形的三边长的是( ).A、 , , B、5,6,7 C、 , , D、6,8,113. 已知:四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是A、 , B、 , C、 , D、 ,4. 若菱形ABCD的周长为16,面积为8,则∠ABC的度数为( )A、30° B、150° C、30°或150° D、30°或120°5. 若函数和函数的图象如图所示,则关于x的不等式的解集是( )
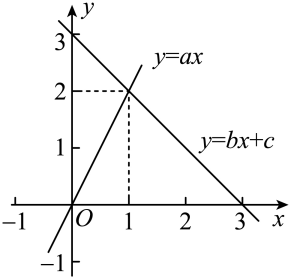 A、 B、 C、 D、6. 五名同学进行投篮练习,规定每人投次,统计他们每人投中的次数,得到个数据,若这个数据的中位数是 , 唯一众数是设另外两个数据分别是 , , 则的值不可能是( )A、 B、 C、 D、7. 若点 , 都在直线上,则下列大小关系成立的是( ).A、 B、 C、 D、8. 已知一次函数 , 若随着的增大而减小,且它的图象与轴交于负半轴,则直线的大致图象是( )A、
A、 B、 C、 D、6. 五名同学进行投篮练习,规定每人投次,统计他们每人投中的次数,得到个数据,若这个数据的中位数是 , 唯一众数是设另外两个数据分别是 , , 则的值不可能是( )A、 B、 C、 D、7. 若点 , 都在直线上,则下列大小关系成立的是( ).A、 B、 C、 D、8. 已知一次函数 , 若随着的增大而减小,且它的图象与轴交于负半轴,则直线的大致图象是( )A、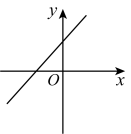 B、
B、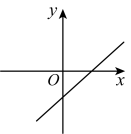 C、
C、 D、
D、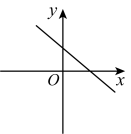 9. 如果顺次连接一个四边形的各边中点所得到的四边形是矩形,那么这个四边形一定是( )A、矩形 B、菱形 C、对角线垂直的四边形 D、对角线相等的四边形10. 如图,在矩形中, , , 点在上,点在上,且 , 连接 , , 则的最小值为( )
9. 如果顺次连接一个四边形的各边中点所得到的四边形是矩形,那么这个四边形一定是( )A、矩形 B、菱形 C、对角线垂直的四边形 D、对角线相等的四边形10. 如图,在矩形中, , , 点在上,点在上,且 , 连接 , , 则的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若正比例函数(k是常数,)的图象经过第二、四象限,则k的值可以是(写出一个即可).12. 某商场为了招聘商品拆装上架员工一名,设置了计算机、语言和商品知识三项测试,并对这三项测试成绩分别赋权2,3,5.若某应试者三项测试成绩分别为70,50,80,则该应试者的平均成绩是 .13. 当时,代数式的值是 .14. 的对角线、相交于点 , , .(1)、若 , 则的面积等于 ;(2)、若 , 则的面积等于 .
三、解答题
-
15. 计算16. 一组数据从小到大的顺序排列: , , , , , , 若这组数据的中位数为 , 求这组数据的方差.17. 如图,在矩形中,将沿着折叠至的位置,点在对角线上,若 , , 求线段的长.
 18. 已知某一次函数的图象与轴的交点坐标为 , 当时, .(1)、求一次函数的解析式;(2)、将该函数的图象沿轴向右平移个单位,求平移后的图像与坐标轴围成三角形面积.19. 在中, . 点D是边AB上的一点,连接CD.作 , , 连接ED.
18. 已知某一次函数的图象与轴的交点坐标为 , 当时, .(1)、求一次函数的解析式;(2)、将该函数的图象沿轴向右平移个单位,求平移后的图像与坐标轴围成三角形面积.19. 在中, . 点D是边AB上的一点,连接CD.作 , , 连接ED.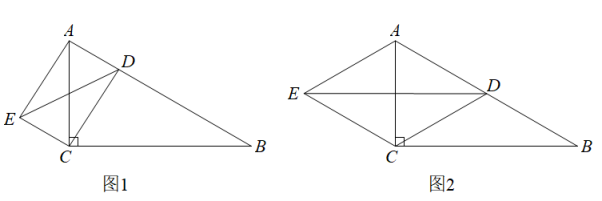 (1)、如图1,当时,求证:;(2)、如图2,当D是边AB的中点时,若 , , 求四边形ADCE的面积.20. 某校名学生参加植树活动,要求每人植棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,:棵;:棵;:棵;:棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2).
(1)、如图1,当时,求证:;(2)、如图2,当D是边AB的中点时,若 , , 求四边形ADCE的面积.20. 某校名学生参加植树活动,要求每人植棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,:棵;:棵;:棵;:棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2).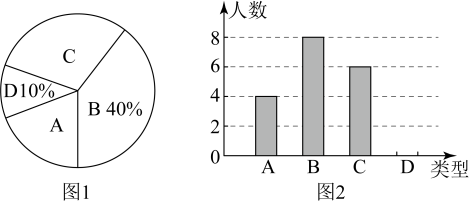
回答下列问题:
(1)、在这次调查中类型有多少名学生?(2)、写出被调查学生每人植树量的众数、中位数;(3)、求被调查学生每人植树量的平均数,并估计这名学生共植树多少棵?21. 县和县分别有某种库存机器台和台,现决定支援村台,村台,已知从县调运一台机器到村和村的运费分别是元和元;从县调运一台机器到村和村的运费分别是元和元.(1)、设县运往村机器台,求总运费关于的函数关系式;(2)、若要求总运费不超过元,共有几种调运方案?哪种调运方案运费最低?22. A,B两地距离24km,甲、乙两人同时从A地出发前往B地.甲先匀速慢走2h,而后匀速慢跑;乙始终保持匀速快走,设运动时间为x(单位:h).甲、乙距离A地的路程分别为 , (单位:km), , 分别与x的函数关系如图所示.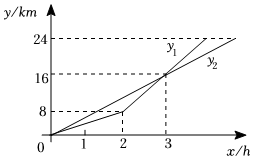 (1)、求关于x的函数解析式;(2)、相遇前,是否存在甲、乙两人相距1km的时刻?若存在,求运动时间;若不存在,请说明理由.23. 已知 , 点为射线上一动点(不与点重合),关于的轴对称图形为 .
(1)、求关于x的函数解析式;(2)、相遇前,是否存在甲、乙两人相距1km的时刻?若存在,求运动时间;若不存在,请说明理由.23. 已知 , 点为射线上一动点(不与点重合),关于的轴对称图形为 .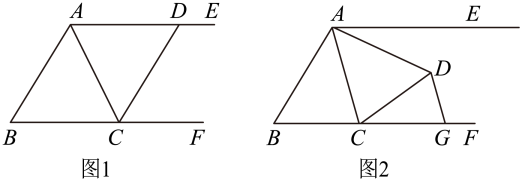 (1)、如图 , 当点在射线上时,求证:四边形是菱形;(2)、如图 , 当点在射线 , 之间时,若点为射线上一点,点为的中点,且 , , , 求的长.
(1)、如图 , 当点在射线上时,求证:四边形是菱形;(2)、如图 , 当点在射线 , 之间时,若点为射线上一点,点为的中点,且 , , , 求的长.