安徽省淮南市谢家集区等三地2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-29 类型:期末考试
一、单选题
-
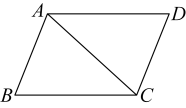
1. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、2. 如图,在平行四边形中, , , 则的度数是( )
 A、 B、 C、 D、3. 点在一次函数的图象上,则的值是( )A、2 B、3 C、4 D、54. 《义务教育课程标准(2022年版)》首次把学生学会炒菜纳入劳动教育课程,并做出明确规定.某班有7名学生已经学会炒的菜品的种数依次为:3,5,4,6,3,3,4,则这组数据的众数和中位数分别是( )A、3,4 B、4,3 C、3,3 D、4,45. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为( )
A、 B、 C、 D、3. 点在一次函数的图象上,则的值是( )A、2 B、3 C、4 D、54. 《义务教育课程标准(2022年版)》首次把学生学会炒菜纳入劳动教育课程,并做出明确规定.某班有7名学生已经学会炒的菜品的种数依次为:3,5,4,6,3,3,4,则这组数据的众数和中位数分别是( )A、3,4 B、4,3 C、3,3 D、4,45. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为( ) A、0.7米 B、1.5米 C、2.2米 D、2.4米6. 下列命题是假命题的是( )A、矩形的对角线互相平分且相等 B、一次函数 的图象不经过第四象限 C、若 , 则 D、若点 , 在直线上,则7. 下列给出的条件中,能判断四边形ABCD是平行四边形的是( )A、AB∥CD,AD=BC B、∠B=∠C;∠A=∠D C、AB=AD,CB=CD D、AB=CD,AD=BC8. 如图,正方形中,点E为上一点,与交于点F,连接 , 若 , 则的度数为( )
A、0.7米 B、1.5米 C、2.2米 D、2.4米6. 下列命题是假命题的是( )A、矩形的对角线互相平分且相等 B、一次函数 的图象不经过第四象限 C、若 , 则 D、若点 , 在直线上,则7. 下列给出的条件中,能判断四边形ABCD是平行四边形的是( )A、AB∥CD,AD=BC B、∠B=∠C;∠A=∠D C、AB=AD,CB=CD D、AB=CD,AD=BC8. 如图,正方形中,点E为上一点,与交于点F,连接 , 若 , 则的度数为( )
 A、 B、 C、 D、9. 如图,在同一平面直角坐标系中,一次函数与 , 小聪根据图象得到如下结论:
A、 B、 C、 D、9. 如图,在同一平面直角坐标系中,一次函数与 , 小聪根据图象得到如下结论:①;②关于x,y的方程组的解为;③关于x的方程的解为;④关于x的不等式的解集是 .
其中结论正确的个数是( )
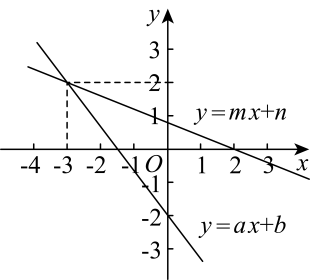 A、1 B、2 C、3 D、410. 如图1,在中,点P从点C出发,设点P的运动距离为x,的长为y,则当点P为中点时,的长为( )
A、1 B、2 C、3 D、410. 如图1,在中,点P从点C出发,设点P的运动距离为x,的长为y,则当点P为中点时,的长为( )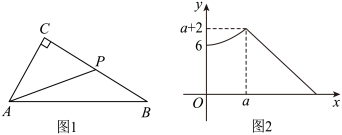 A、5 B、 C、 D、8
A、5 B、 C、 D、8二、填空题
-
11. 写出在函数的图象上的一个点的坐标 .12. 在甲、乙两位射击运动员的10次考核成绩中,两人的考核成绩的平均数相同,方差分别为 , , 则考核成绩更为稳定的运动员是 . (填“甲”或“乙”)13. 已知平行四边形的周长为 , 若 , 则的长为 .14. 每年的4月23日是“世界读书日”,某校为了解4月份八年级学生的读书情况,随机调查了八年级50名学生读书的册数,由此估计该校八年级学生4月份人均读书册.
册数
0
1
2
3
4
人数
9
3
20
15
3
15. 若为的小数部分,则的值为 .16. 将直线平移,使其经过点 , 则平移后所得直线的解析式为 .17. 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,两车的距离y(千米)与慢车行驶的时间x(小时)之间的函数关系如图所示,则快车到达乙地时慢车离乙地距离为 千米.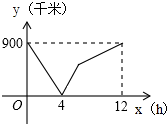
三、解答题
-
18. 如图,菱形的边长为4,(不与A,D重合),点F是边上一动点,且 .
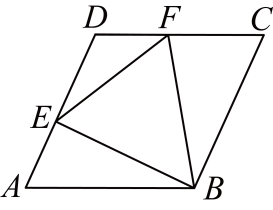
①的度数为;
②面积的最小值为 .
19. 计算:(1)、;(2)、 .20. 已知 是关于的一次函数,且当时,;时, .(1)、求一次函数的解析式;(2)、当时,求自变量的值.21. 每年的4月15日是我国全民国家安全教育日.某中学在全校七、八年级共800名学生中开展“国家安全法”知识竞赛,并从七、八年级学生中各抽取20名学生,统计这部分学生的竞赛成绩(竞赛成绩均为整数,满分10分,6分及以上为合格)八年级抽取的学生的竞赛成绩:4,4,6,6,6,6,7,7,7,8,8,8,8,8,8,9,9,9,10,10.
七年级抽取的学生的竞赛成绩条形统计图七、八年级抽取的学生的竞赛成绩统计表
年级
七年级
八年级
平均数
a
7.4
中位数
b
8
众数
7
c
合格率
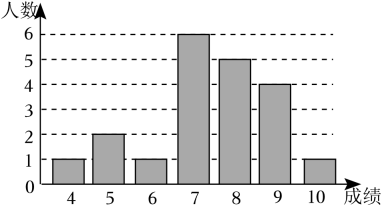
根据以上信息,解答下列问题:
(1)、填空:;; .(2)、估计该校七、八年级共800名学生中竞赛成绩不合格的人数;(3)、在这次“国家安全法”知识竞赛中,你认为哪个年级的学生成绩更优异?请说明理由(一条理由即可).22. 在“一带一路”战略的影响下,某茶叶经销商准备把“茶路”融入“丝路”,经计算,他销售每千克A级茶,B级茶的利润分别为100元,150元.若该经销商决定购进A,B两种级别的茶叶共200千克用于出口,设购进A级茶x千克,销售总利润为y元.(1)、求y与x之间的函数关系式;(2)、若其中B级别茶叶的进货量不超过A级别茶叶的4倍,请你帮该经销商设计一种进货方案使销售总利润最大,并求出总利润的最大值.23. 如图,在四边形中 , 为对角线的中点,过点作直线分别与边 , 交于 , 两点,连接 , .
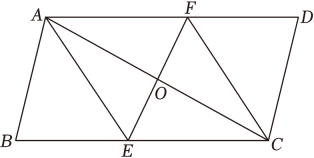 (1)、求证:四边形是平行四边形;(2)、当平分时,
(1)、求证:四边形是平行四边形;(2)、当平分时,①试说明四边形是菱形;
②当四边形是矩形时,若 , , 求的长.