吉林省白城市通榆县2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-29 类型：期末考试

进入出卷网下载

一、单选题

1. 函数 $y = \sqrt{x - 3}$ 中，自变量x的取值范围是（）

A、x≠3 B、x≥3 C、x＞3 D、x≤3

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{15} \div 3 = \sqrt{5}$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 ${(2 \sqrt{3})}^{2} = 6$

查看试题解析
3. 如图，由下列条件不能判定为直角三角形的是（）

A、 $∠ A + ∠ B = ∠ C$ B、 $c^{2} - b^{2} = a^{2}$ C、 $a = 3$ ， $b = 4$ ， $c = 5$ D、 $∠ A ： ∠ B ： ∠ C = 1 ： 1 ： 4$

查看试题解析
4. 如图，在菱形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点O，下列结论中不一定成立的是（）

A、 $A B ∥ C D$ B、 $A C = B D$ C、 $A C ⊥ B D$ D、 $O A = O C$

查看试题解析
5. 如图，在 $▱ A B C D$ 中，已知 $A D = 5 c m$ ， $A B = 4 c m$ ， $A E$ 平分 $∠ B A D$ 交 $B C$ 边于点E，则 $E C$ 等于（）

A、1 $c m$ B、2 $c m$ C、3 $c m$ D、4 $c m$

查看试题解析
6. 若 $m < 0$ ， $n < 0$ ，则 $y = m x + n$ 的图像可能是（）

A、 B、 C、 D、

查看试题解析

二、填空题

7. 计算： $\sqrt{14} \times \sqrt{2}$ ＝.

查看试题解析
8. 将直线 $y = 2 x$ 向下平移5个单位长度，所得直线的解析式是．

查看试题解析
9. 测量7名学生的体温（单位： $℃$ ）如下： $36.5$ ， $36.3$ ， $36.8$ ， $36.3$ ， $36.5$ ， $36.7$ ， $36.5$ ，这组数据的众数是．

查看试题解析
10. 某汽车油箱中原有油量为 $42 L$ ，每km的耗油量为0.07升，油箱中的余油量 $y$ （L）与汽车行驶里程数 $x$ （km）之间的函数关系式是（ $0 \leq x \leq 600$ ）．

查看试题解析
11. 有甲、乙两名学员练习射击，第一轮10枪打完后两人打靶的环数如图所示，则甲、乙两人这10次射击环数的方差大小关系为 $s_{甲}^{2}$ $s_{乙}^{2}$ （填 $>$ 或 $<$ 或 $=$ ）．

查看试题解析
12. 已知一个直角三角形的两条直角边分别为6，8，那么这个直角三角形斜边上的高为．

查看试题解析
13. 如图，DE为△ABC的中位线，点F在DE上，且∠AFB＝90°，若AB＝5，BC＝8，则EF的长为．

查看试题解析
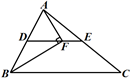14. 如图，在正方形 $A B C D$ 中，E为 $C D$ 边上一点，将 $△ A E D$ 沿着AE翻折得到 $△ A E F$ ，点D的对应点F恰好落在对角线 $A C$ 上，连接 $B F$ ，若 $E F = 2$ ，则 $B F^{2} =$ ．

查看试题解析

三、解答题

15. 计算： $\sqrt{12} - \sqrt{27} + \sqrt{\frac{1}{3}}$ ．

查看试题解析
16. 若 $x < 2$ ，化简 $\sqrt{x^{2} - 4 x + 4} + | 4 - x |$ ，小明的解答过程如下：
解：原式 $= \sqrt{{(x - 2)}^{2}} + (4 - x)$ 第一步
$= x - 2 + 4 - x$ 第二步
$= 2$ 第三步

(1)、小明的解答从第步出现错误的，错误的原因是用错了性质：；

(2)、写出正确的解答过程．

查看试题解析
17. 如图，一架梯子 $A B$ 长2.5米，顶端A靠在垂直于地面的墙 $A C$ 上，这时梯子下端B离墙角C的距离为1.5米，梯子滑动后停在 $D E$ 的位置上，测得 $B D$ 长为0.9米，计算梯子顶端A下滑的距离．

查看试题解析
18. 如图，在 $▱ A B C D$ 中， $A E ⊥ B C$ 于E，点F在边 $A D$ 上， $B E = D F$ ，求证：四边形 $A E C F$ 是矩形.

查看试题解析
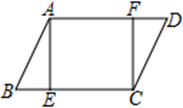19. 如图是边长为1的小正方形网格，每个小正方形的顶点叫做格点，只用无刻度的直尺在网格中完成下列画图．

(1)、如图①，A，C均在格点处， $A C = 5$ ，在图①中过点A画出线段 $A B$ ，使 $A B = A C$ （点B在格点上），并且 $A B$ 在 $A C$ 上方（画出所有满足条件的 $A B$ ）；

(2)、如图②中， $▱ A B C D$ 的顶点A、B、C、D均在格点处，点E是线段 $A D$ 中点，在线段 $B C$ 上找到一点F，连接 $E F$ ，使 $E F ∥ A B$ ．

查看试题解析
20. 如图所示，已知直线 $y = k x + b$ 经过点 $A (5 ， 0)$ ， $B (1 ， 4)$ ．

(1)、求直线 $A B$ 的解析式；

(2)、若直线 $y = 2 x - 4$ 与直线 $A B$ 相交于点C，求点C的坐标；

(3)、根据图象，直接写出关于 $x$ 的不等式 $2 x - 4 > k x + b$ 的解集．

查看试题解析
21. 如图所示，A，B两块试验田相距200m，C为水源地，AC=160m，BC=120m，为了方便灌溉，现有两种方案修筑水渠。
甲方案：从水源地C直接修筑两条水渠分别到A，B。

乙方案：过点C作AB的垂线，垂足为H，先从水源地C修筑一条水渠到AB所在直线上的H处，再从H分别向A，B进行修筑。

(1)、请判断△ABC的形状(要求写出推理过程)。

(2)、两种方案中，哪一种方案所修的水渠较短？请通过计算说明。

查看试题解析
22. 如图，已知矩形ABCD的对角线交于点O，点E、F和G分别平分线段AB、OD和OA．

(1)、求证：四边形OFGE是平行四边形．

(2)、猜想：当 $∠ A B D =$ ▲ °时四边形OFGE是菱形，并证明．

查看试题解析
23. 某医药公司把一批药品运往外地，现有两种运输方式可供选择．
方式一：使用快递公司的邮车运输，装卸收费400元，另外每千米再加收4元；
方式二：使用快递公司的火车运输，装卸收费820元，另外每千米再加收2元．

(1)、请你分别写出邮车、火车运输的总费用y₁（元），y₂（元）与路程x（km）之间的函数解析式；

(2)、你认为选用哪种运输方式较好，为什么？

查看试题解析
24. 为深入领会“习近平新时代中国特色社会主义思想”精髓，我市组织党员开展一次“习近平新时代中国特色社会主义思想”知识竞赛，为了解本次竞赛的成绩分布情况，随机抽取了男生和女生各20名党员的竞赛成绩作为样本进行整理，规定：满分10分，成绩达到8分或8分以上为优秀，达到6分或6分以上为合格，6分以下为不合格（每名党员竞赛得分均为整数）．下面给出了部分信息：
信息一：抽取的男生的成绩分别是：
10，10，10， 9，9，9，9，9，9，9，8，8，8，8，7，7，6，6，5，4；
信息二：下图是抽取的女生成绩的不完整统计图；
信息三：被抽取的男生、女生的各统计量如下表：


平均数
中位数
众数
满分率
优秀率
合格率
男生
8
          $a$
9
15%
          $c$
90%
女生
8.05
8
          $b$
20%
75%
90%
认真阅读以上信息，解答下列问题：

(1)、 $a =$ ， $b =$ ， $c =$ ；

(2)、请补全条形统计图；

(3)、我市共有男生420人，女生400人参加比赛，请你估计一下本次知识竞赛达到优秀的党员人数．

查看试题解析
25. 已知A，B两地之间有一条长240千米的公路．甲车从A地出发匀速开往B地，甲车出发两小时后，乙车从B地出发匀速开往A地，两车同时到达各自的目的地，两车行驶的路程之和y（千米）与甲车行驶的时间x（小时）之间的函数关系如图所示．

(1)、甲车的速度为千米/小时，a的值为；

(2)、求乙车出发后，y与x之间的函数关系式，并写出自变量x的取值范围；

(3)、当乙车行驶2.5小时时，求甲、乙两车之间的距离．

查看试题解析
26. 如图①，在四边形ABCD中， $A D ∥ B C$ ， $∠ A = 90 °$ ， $A D = 6$ ， $B C = 9$ ， $C D = 5$ ，点P从点A出发，沿射线AD以每秒2个单位长度的速度运动，点Q从点C出发，沿CB方向以每秒1个单位长度的速度向终点B运动，P、Q两点同时出发，当点Q到达点B时，点P也随之停止运动，设点Q运动时间为t秒．

(1)、AB的长为．

(2)、求线段PD的长（用含t的代数式表示）．

(3)、当以P、D、C、Q为顶点的四边形为平行四边形时，求t的值．

(4)、如图②，若点E为BC边上一点，且 $B E = 5$ ，当 $△ P B E$ 是以BE为腰的等腰三角形时，直接写出t的值．

查看试题解析

	平均数	中位数	众数	满分率	优秀率	合格率
男生	8	$a$	9	15%	$c$	90%
女生	8.05	8	$b$	20%	75%	90%