吉林省四平市伊通满族自治县2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-29 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，最简二次根式的是（）

A、 $\sqrt{\frac{1}{5}}$ B、 $\sqrt{0.5}$ C、 $\sqrt{5}$ D、 $\sqrt{50}$

查看试题解析
2. 若y=x+2–b是正比例函数，则b的值是（）

A、0 B、–2 C、2 D、–0.5

查看试题解析
3. 如果一个三角形，三条边的长度之比为 $3 ： 4 ： 5$ ，且周长为 $48 c m$ ，那么这个三角形的面积是（）

A、 $48 c m^{2}$ B、 $96 c m^{2}$ C、 $192 c m^{2}$ D、 $220 c m^{2}$

查看试题解析
4. 一次函数 $y = 4 x + 4$ 的图象不经过的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 如图，在平行四边形 $A B C D$ 中， $A B = 3$ ， $B C = 4$ ， $A C$ 的垂直平分线交 $A D$ 边于点 $E$ ，则 $△ C D E$ 的周长是（）

A、6 B、7 C、8 D、10

查看试题解析
6. 在某次数学质量监测中，八年一班数学老师随机抽取了10份试卷，成绩表中所显示的分数如下：105，101，109，101，92，102，97，101，99，103，则这组数据的中位数是（）

A、101 B、 $96.5$ C、97 D、102

查看试题解析

二、填空题

7. 现有甲、乙两支排球队，每支球队队员身高的平均数均为1.85米，方差分别为 $S_{甲}^{2} = 0.32$ ， $S_{乙}^{2} = 0.26$ ，则身高较整齐的球队是队．

查看试题解析
8. 已知函数 $y = 4 x - 4$ 的图象经过点 $A (5 ， y_{1})$ ，点 $B (2 ， y_{2})$ ，则 $y_{1}$ $y_{2}$ （填“＞”或“＜”或“＝”）．

查看试题解析
9. 综合实践活动社团的同学们要制作一个风筝，需要一块等腰三角形纸板，已知这个等腰三角形的腰长为10，底边上的高为8，请你帮助他们计算出这个等腰三角形的底边长应为．

查看试题解析
10. 若 $\sqrt{4 - x} + \sqrt{x - 4}$ 在实数范围内有意义，则 $\sqrt{x^{2}} =$ ．

查看试题解析
11. 如果直线 $y = - 2 x + k$ 与两坐标轴所围成的三角形的面积是9，那么 $k$ 的值为．

查看试题解析
12. 如图：在 $△ A B C$ 中， $∠ C = 90 °$ ， $B D$ 是 $△ A B C$ 的角平分线，过点 $D$ 作线段 $D E$ ，使 $D E ∥ A B$ 交 $B C$ 于点 $E$ ， $F$ 为 $A B$ 上一点，连接 $D F$ ， $E F$ ，已知 $D C = 5$ ， $C E = 12$ ，则 $△ D E B$ 的面积是．

查看试题解析
13. 如图，已知平行四边形 $A B C D$ 的对角线 $A C$ 与 $B D$ 相交于点 $O$ ， $A B ⊥ A C$ ，若 $A B = 4$ ， $A C = 6$ ，则 $B D$ 的长是．

查看试题解析
14. 如图，CD $∥$ BE，且 $C D = \frac{1}{2} A B$ ，点 $E$ 为 $A B$ 的中点，若四边形 $A D C E$ 为正方形，则 $∠ B =$ ．

查看试题解析

三、解答题

15. 计算： $\sqrt{12} - 9 \sqrt{\frac{1}{3}} + \sqrt{48}$ ．

查看试题解析
16. 先化简，再求值： $(\frac{1}{a - 1} - \frac{1}{a + 1}) \cdot \frac{a^{2} - 1}{a}$ ，其中 $a = \sqrt{2}$

查看试题解析
17. 一种机器零件的形状如图所示，按规定这个零件中 $∠ A$ 和 $∠ D B C$ 都应为直角才符合要求，工人师傅量得这个零件各边尺寸如图．请你判断这个零件符合要求吗？并说明理由．

查看试题解析
18. 如图，将矩形 $A B C D$ 沿对角线 $A C$ 折叠，点B的对应点为点E， $A E$ 与 $C D$ 交于点F.
求证： $△ D A F ≌ △ E C F$ .

查看试题解析
19. 如图，在菱形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 交于点O， $D E ∥ A C$ ， $C E ∥ B D$ ．求证：四边形 $O C E D$ 是矩形．

查看试题解析
20. 已知一次函数 $y = k x + b$ 的图象经过 $A (2 ， 4)$ ， $B (0 ， 2)$ 两点，并且与 $x$ 轴相交于点 $P$ ，求： $k$ 和 $b$ 的值及 $P$ 点的坐标．

查看试题解析
21. 如图，某海滨浴场岸边A处救生员发现海中的 $B$ 处有人求救，救生员没有直接从 $A$ 处游向 $B$ 处，而是沿岸边自A处跑到离 $B$ 处最近的点 $C$ ，然后从点 $C$ 游向 $B$ 处，经测量 $A C = 400 m$ ， $B C = 300 m$ ，若救生员在岸边行进的速度是 $5 m / s$ ，在海中行进的速度是 $2 m / s$ ，请分析救生员的选择合理吗？

查看试题解析
22. 近几年来全国各省市市政府民生实事之一的公共自行车建设工作已基本完成．某市某部门对 $2017$ 年， $10$ 月份中的 $7$ 天进行了公共自行车日租车辆的统计，结果如图．

(1)、这 $7$ 天日租车辆的众数是，中位数是；

(2)、求这 $7$ 天日租车辆的平均数；

(3)、用（2）中的平均数估计 $10$ 月份该市共租车多少万车次？

查看试题解析
23. “五一”长假小明一家由爸爸驾车到某景区进行游玩，汽车出发前油箱内有油 $50 L$ ，行驶若干小时后，在加油站加油若干升，油箱中剩余油量y（单位：L）与行驶时间 $t$ （单位：h）之间的关系如图所示，请你根据图象回答下列问题：

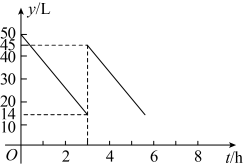(1)、汽车行驶h后加油，加油L；

(2)、求加油前油箱剩余油量y与行驶时间t的函数解析式；

(3)、已知加油前后汽车都以 $60 k m / h$ 的速度匀速行驶且路况相同，如果加油站距景区还有 $240 k m$ ，请你判断油箱中的油是否够用？请说明理由．

查看试题解析
24. 如图

(1)、感知：如图（1）所示，四边形 $A B C D$ 是正方形，点 $G$ 是线段 $B C$ 上的任意一点， $D E ⊥ A G$ 于点 $E$ ， $B F ∥ D E$ ，且交 $A G$ 于点 $F$ ，求证： $A F - B F = E F$ ．

(2)、探究一：如图（2）所示，若点 $G$ 在 $C B$ 的延长线上，上述其余条件不变，则 $A F$ ， $B F$ ， $E F$ 存在怎样的等量关系？猜想并证明这一结论．

(3)、探究二：若点 $G$ 在 $B C$ 的延长线上，上述其余条件不变，则 $A F$ ， $B F$ ， $E F$ 又存在怎样的等量关系？直接写出结论．

查看试题解析