上海市徐汇区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-29 类型:期末考试
一、单选题
-
1. 下列函数中,一次函数是( )A、 B、 C、 D、2. 一次函数在轴上的截距是( )A、 B、 C、 D、3. 下列各式错误的是( )A、 B、 C、 D、4. 一次函数的图象不经过的象限是 ( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列事件中,属于确定事件的是( )A、抛一枚硬币,落地后正面朝上 B、菱形的两条对角线相等 C、两个非零实数的积为正 D、10只鸟关在3个笼子里,至少有一个笼子关的鸟超过3只6. 在四边形中, . 如果再添加一个条件可推出四边形是正方形,那么这个条件可以是( )A、 B、 C、 D、
二、填空题
-
7. 将直线平移,使平移后的直线经过点 , 所得直线的表达式是 .8. 方程的根是 .9. 方程 的解为 .
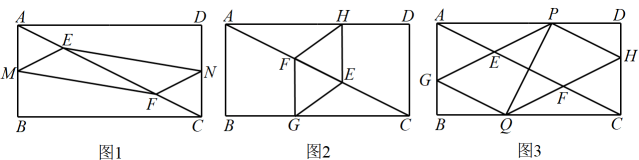
10. 在分式方程中,令 , 则原方程可化为关于y的方程是 .11. 图形的密铺(或称图形的镶嵌)指用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间既不留空隙、也不互相重叠地把一部分平面完全覆盖.图1所示的是一种五边形密铺的结构图,图2是从该密铺图案中抽象出的一个五边形,其中 , , 则的度数是 . 12. 一次函数y=kx+b的图象如图所示,当y>0时,x的取值范围是
12. 一次函数y=kx+b的图象如图所示,当y>0时,x的取值范围是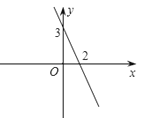 13. 某市出租车的收费起步价为14元,即路程不超过3公里时收费14元,超过部分每公里收费2.4元.如果乘客乘坐出租车行驶的路程为x(x>3)公里,乘车费为y元,那么y与x之间的关系式为 .14. 如图,在△ABC中,E、F分别是AB、AC的中点,若BF平分∠ABC,BC=6,则BE的长为.
13. 某市出租车的收费起步价为14元,即路程不超过3公里时收费14元,超过部分每公里收费2.4元.如果乘客乘坐出租车行驶的路程为x(x>3)公里,乘车费为y元,那么y与x之间的关系式为 .14. 如图,在△ABC中,E、F分别是AB、AC的中点,若BF平分∠ABC,BC=6,则BE的长为.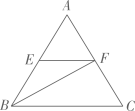 15. 如下图,长为6,宽为3的矩形 , 阴影部分的面积为.
15. 如下图,长为6,宽为3的矩形 , 阴影部分的面积为. 16. 已知在等腰梯形中, , , 垂足为点O,如果 , 那么梯形的上下底之和等于 .
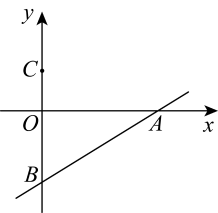
16. 已知在等腰梯形中, , , 垂足为点O,如果 , 那么梯形的上下底之和等于 .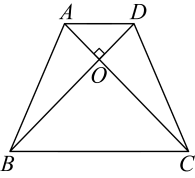 17. 我们把两条对角线长度之比为的菱形叫做“钻石菱形”,如果一个“钻石菱形”的面积为8,那么它的边长是 .18. 如图,中,//轴, . 点A的坐标为 , 点D的坐标为 , 点B在第四象限,点G是AD与y轴的交点,点P是CD边上不与点C,D重合的一个动点,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,点P的坐标为 .
17. 我们把两条对角线长度之比为的菱形叫做“钻石菱形”,如果一个“钻石菱形”的面积为8,那么它的边长是 .18. 如图,中,//轴, . 点A的坐标为 , 点D的坐标为 , 点B在第四象限,点G是AD与y轴的交点,点P是CD边上不与点C,D重合的一个动点,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,点P的坐标为 .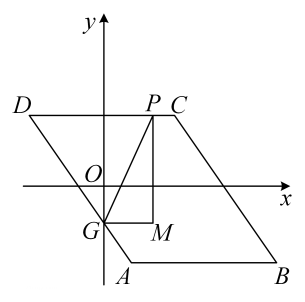
三、解答题
-
19.20. 解方程组:21. 如图,四边形和四边形都是平行四边形,
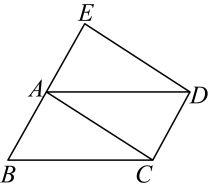 (1)、填空:=;;(2)、求作: .22. 有两个不透明的袋子分别装有除颜色外其余均相同的小球,甲袋中有1个红球和2个白球,乙袋中有2个红球和1个白球.(1)、如果在甲袋中摸出一个小球,那么摸到黑球是(填“确定事件”或“随机事件”);(2)、如果在乙袋中摸出一个小球,那么摸到红球或白球的概率是;(3)、如果在甲、乙两个袋子中分别随机摸出一个小球,那么摸到两球颜色相同的概率是多少?(请用列表法或树形图法说明)23. 某商店以2400元购进某种盒装茶叶,第一个月每盒按进价增加作为售价,售出50盒,第二个月每盒以低于进价5元作为售价,售完余下的茶叶.在整个买卖过程中盈利350元,求每盒茶叶的进价.24. 如图,△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交线段DE的延长线相交于F点,取AF的中点G , 如果BC=2AB .
(1)、填空:=;;(2)、求作: .22. 有两个不透明的袋子分别装有除颜色外其余均相同的小球,甲袋中有1个红球和2个白球,乙袋中有2个红球和1个白球.(1)、如果在甲袋中摸出一个小球,那么摸到黑球是(填“确定事件”或“随机事件”);(2)、如果在乙袋中摸出一个小球,那么摸到红球或白球的概率是;(3)、如果在甲、乙两个袋子中分别随机摸出一个小球,那么摸到两球颜色相同的概率是多少?(请用列表法或树形图法说明)23. 某商店以2400元购进某种盒装茶叶,第一个月每盒按进价增加作为售价,售出50盒,第二个月每盒以低于进价5元作为售价,售完余下的茶叶.在整个买卖过程中盈利350元,求每盒茶叶的进价.24. 如图,△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交线段DE的延长线相交于F点,取AF的中点G , 如果BC=2AB .
求证 :
(1)、四边形ABDF是菱形;(2)、AC=2DG .