四川省乐山市市中区中区2022-2023学年八年级下学期教学质量监测数学试题

试卷更新日期：2023-08-29 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式： $\frac{1}{x}$ ， $\frac{1}{2} (x + y)$ ， $\frac{x}{π}$ ， $\frac{2}{x - y}$ ，其中分式有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 若分式 $\frac{2}{x - 1}$ 有意义，则（）

A、 $x \neq 0$ B、 $x \neq - 1$ C、 $x \neq 1$ D、 $x \neq 2$

查看试题解析
3. 如图，在平行四边形 $A B C D$ 中， $∠ A = ∠ D + 40 °$ ，则 $∠ B =$ （）

A、 $70 °$ B、 $60 °$ C、 $50 °$ D、 $40 °$

查看试题解析
4. 已知菱形 $A B C D$ 的两条对角线 $A C 、 B D$ 的长分别是 $6 c m$ 和 $8 c m$ ，则菱形 $A B C D$ 的面积为（）

A、 $48 c m^{2}$ B、 $36 c m^{2}$ C、 $24 c m^{2}$ D、 $12 c m^{2}$

查看试题解析
5. 已知关于x的分式方程 $\frac{m + 3}{2 x - 1} = 1$ 的解为非负数，则m的取值范围是（）

A、 $m \geq - 4$ B、 $m \geq - 4$ 且 $m \neq - 3$ C、 $m > - 4$ D、 $m > - 4$ 且 $m \neq - 3$

查看试题解析
6. 在平行四边形的复习课上，小明绘制了如下知识框架图，箭头处添加条件错误的是（）

A、①：对角线相等 B、②：对角互补 C、③：一组邻边相等 D、④：有一个角是直角

查看试题解析
7. 如图，在矩形 $A B C D$ 中， $A B = 1$ ，对角线 $A C$ 与 $B D$ 相交于点O， $A E ⊥ B D$ 于E，若 $B E = E O$ ，则 $A D$ 的长是（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、2 D、3

查看试题解析
8. 若点 $A (- 1 ， y_{1})$ 、 $B (2 ， y_{2})$ 、 $C (π ， y_{3})$ 在反比例函数 $y = \frac{5}{x}$ 的图象上，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系是（）

A、 $y_{3} < y_{2} < y_{1}$ B、 $y_{2} < y_{3} < y_{1}$ C、 $y_{1} < y_{3} < y_{2}$ D、 $y_{1} < y_{2} < y_{3}$

查看试题解析
9. 函数 $y = k x - k$ 与 $y = \frac{k}{x}$ 在同一平面直角坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析
10. 如图，正方形 $A B C D$ 的边长为4，G是对角线 $B D$ 上一动点， $G E ⊥ C D$ 于点 $E$ ， $G F ⊥ B C$ 于点 $F$ ，连接 $E F$ ，给出四种情况：
①若G为 $B D$ 的中点，则四边形 $C E G F$ 是正方形；②若G为 $B D$ 上任意一点，则 $A G = E F$ ；③点G在运动过程中， $G E + G F$ 的值为定值4；④点G在运动过程中，线段 $E F$ 的最小值为 $2 \sqrt{2}$ ．

A、①②③④ B、①②③ C、①②④ D、①③④

查看试题解析

二、填空题

11. 生物具有遗传多样性，遗传信息大多储存在DNA分子上．一个DNA分子的直径约为0.000000301cm．用科学记数法可表示为cm．

查看试题解析
12. 已知分式 $\frac{2 a}{a + b} = 3$ ，若把a，b的值都扩大到原来的3倍，此时分式的值为（填数字）

查看试题解析
13. 如图，在平行四边形 $A B C D$ 中， $E F$ 过对角线的交点O，若 $A B = 4$ ， $B C = 5$ ， $O E = \frac{3}{2}$ ，则四边形 $C D E F$ 的周长是．

查看试题解析
14. 若直线 $y = k x + b (k \neq 0)$ 经过点 $A (- 2 ， 3)$ ，且与y轴的交点在x轴上方，则k的取值范围是．

查看试题解析
15. 如图，点E、F分别是菱形 $A B C D$ 的边 $B C$ 、 $C D$ 上的点，且 $∠ B = ∠ E A F = 60 °$ ， $∠ F A D = 42 °$ ，则 $∠ C E F =$ $°$ ．

查看试题解析
16. 如图， $A (1 ， 3)$ ， $B (3 ， 1)$ 是反比例函数 $y = \frac{3}{x}$ 的图象上的两点，点P是反比例函数 $y = \frac{3}{x}$ 的图象位于线段 $A B$ 下方的一动点，过点P作 $P M ⊥ x$ 轴于M，交线段 $A B$ 于Q．设点M横坐标为x，则 $△ O P Q$ 面积的最大值为，此时 $x =$ ．

查看试题解析

三、解答题

17. 计算： $(- 1)^{2023} + (π - 3)^{0} - {(- \frac{1}{2})}^{- 2}$ ．

查看试题解析
18. 解方程： $\frac{2 x}{x - 1} - 1 = \frac{4}{x - 1}$

查看试题解析
19. 先化简 $\frac{2 a + 2}{a - 1} \div (a + 1) + \frac{a^{2} - 1}{a^{2} - 2 a + 1}$ ，然后a在﹣1，1，2三个数中任选一个合适的数代入求值．

查看试题解析
20. 如图，直线 $l_{1}$ ： $y = x + 1$ 与直线 $l_{2}$ ： $y = m x + 3$ 相交于点 $P (1 ， b)$ ．

(1)、求m、b的值；

(2)、请直接写出关于x、y的方程组 ${\begin{array}{l} y = x + 1 \\ y = m x + 3 \end{array}$ 的解；

(3)、请直接写出关于x的不等式组 ${\begin{array}{l} x + 1 > 0 \\ m x + 3 > 0 \end{array}$ 的解集．

查看试题解析
21. 某药品研究所开发一种抗菌新药，经多年动物实验，首次用于临床人体试验，测得成人服药后血液中药物浓度y（微克/毫升）与服药时间x小时之间函数关系如图所示．

(1)、根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式；

(2)、问血液中药物浓度不低于2微克/毫升的持续时间多少小时？

查看试题解析
22. 为了解某校八年级男生的体能情况，体育老师随机抽取部分男生进行引体向上测试，并对成绩进行了统计，绘制出统计图1和图2，请根据图中信息，解答下列问题：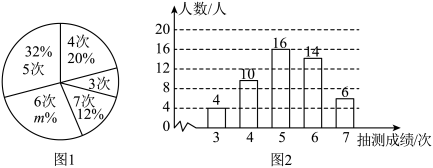

(1)、本次抽测的男生人数为，图1中m的值为；

(2)、求本次抽测的这组数据的平均数、众数和中位数；

(3)、若规定引体向上5次以上（含5次）为体能达标，根据样本数据，估计该校八年级300名男生中有多少人体能达标．

查看试题解析
23. 如图，在平行四边形ABCD中，对角线AC、BD相交于点O，点E、F在线段BD上，且 $B E = D F$ ，连结AE、CE、AF、CF．

(1)、求证：四边形AECF为平行四边形；

(2)、若 $A C ⊥ B D$ ， $∠ A E C = 120 °$ ， $A O = \sqrt{3}$ ，求四边形AECF的周长．

查看试题解析
24. 2022年秋季，中小学开始实施《义务教育劳动课程标准（2022年版）》，向全国中小学生传递了“双减”背景下加强劳动教育的鲜明信号．某校准备到劳动实践基地开展劳动教育，现欲购进甲、乙两种蔬菜苗供学生栽种，已知用400元购进甲种蔬菜苗的数量比用300元购进乙种蔬菜苗的数量多400株，单独购一株乙种蔬菜苗的价格是单独购进一株甲种蔬菜苗价格的1.5倍．

(1)、求购进一株甲种蔬菜苗和一株乙种蔬菜苗各需要多少元；

(2)、学校准备购进两种蔬菜苗共1800株，甲种蔬菜苗不少于1000株，不多于1200株，则学校购买甲、乙两种蔬菜苗的总费用最少需要多少元？

查看试题解析
25. 已知，在矩形 $A B C D$ 中， $A B = 5$ ， $B C = 10$ ，在 $A B$ 上取一点E，使 $A E = 3$ ，点F是 $B C$ 边上的一个动点，以 $E F$ 为一边作菱形 $E F G H$ ，使点H落在 $A D$ 边上，点G落在矩形 $A B C D$ 内或其边上，若 $B F = x$ ， $△ G F C$ 的面积为S．

(1)、如图1，当四边形 $E F G H$ 是正方形时，求x的值；

(2)、如图2，当四边形 $E F G H$ 是菱形时，
①求证： $∠ A H E = ∠ C F G$ ；

②求出S与x的函数关系式并直接写出x的取值范围．

查看试题解析
26. 如图1，直线l与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象交于 $A (- 1 ， 3)$ ， $B (- 3 ， a)$ 两点．

(1)、求反比例函数和直线l的解析式；

(2)、若直线l在反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象上方，请直接写出x的取值范围；

(3)、点M在y轴上，点N为坐标平面内任一点，若以A、B、M、N四点构成的四边形为菱形，请直接写出点N的坐标；

(4)、如图2，直线l与x轴相交于点D，点A关于原点对称的点为E，请用无刻度的直尺和圆规作出 $∠ E A D$ 的平分线 $A P$ （不写作法，保留作图痕迹），过点E作 $E F ⊥ A P$ 于F，连结 $D F$ ，求 $△ A D F$ 的面积．

查看试题解析