四川省成都市邛崃市2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-29 类型:期末考试
一、单选题
-
1. 若分式有意义,那么的取值范围是( )A、 B、 C、 D、2. 已知 , , 则的值为( )A、12 B、 C、25 D、3. 下列图标中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 在平面直角坐标系中有两点 , , 平移线段至某处,若此时点P的对应点的坐标为 , 则点Q的对应点的坐标为( )A、 B、 C、 D、5. 已知直线 , 将以 , 为两腰的等腰的顶点P,N按如图所示的方式分别放在a,b上,若 , , 则( )
4. 在平面直角坐标系中有两点 , , 平移线段至某处,若此时点P的对应点的坐标为 , 则点Q的对应点的坐标为( )A、 B、 C、 D、5. 已知直线 , 将以 , 为两腰的等腰的顶点P,N按如图所示的方式分别放在a,b上,若 , , 则( ) A、 B、 C、 D、6. 在平面直角坐标系中,若点在第三象限,则的取值范围为( )A、 B、 C、 D、7. 如图,的对角线相交于点 , 若 , , , 则的周长为( )
A、 B、 C、 D、6. 在平面直角坐标系中,若点在第三象限,则的取值范围为( )A、 B、 C、 D、7. 如图,的对角线相交于点 , 若 , , , 则的周长为( ) A、36 B、38 C、40 D、428. 为了帮助遭受自然灾害的地区重建家园,某学校号召同学们自愿捐款.已知七年级同学捐款总额为5500元,八年级同学捐款总额为6000元,八年级捐款人数比七年级多30人,而且两个年级人均捐款额恰好相等.如果设七年级捐款人数为人,则所列方程为( )A、 B、 C、 D、
A、36 B、38 C、40 D、428. 为了帮助遭受自然灾害的地区重建家园,某学校号召同学们自愿捐款.已知七年级同学捐款总额为5500元,八年级同学捐款总额为6000元,八年级捐款人数比七年级多30人,而且两个年级人均捐款额恰好相等.如果设七年级捐款人数为人,则所列方程为( )A、 B、 C、 D、二、填空题
-
9. 已知 , 则 . (填“”、“”或“”)10. 已知一个n边形的每一个外角都为30°,则n等于 .11. 如图,在中, , 将绕点逆时针旋转一定的角度至处,此时点E, , 恰好在同一条直线上,连接 , 若 , 则 .
 12. 若多项式的结果是一个多项式的平方,则单项式 . (只填一个你认为正确的答案)13. 如图,在中, , 按以下步骤作图:①以点为圆心,合适的长为半径作弧,分别交于点M,N;②分别以点M,N为圆心,大于的长为半径作弧,两弧在内交于点O;③作射线 , 交于点E.若 , 则的长为 .
12. 若多项式的结果是一个多项式的平方,则单项式 . (只填一个你认为正确的答案)13. 如图,在中, , 按以下步骤作图:①以点为圆心,合适的长为半径作弧,分别交于点M,N;②分别以点M,N为圆心,大于的长为半径作弧,两弧在内交于点O;③作射线 , 交于点E.若 , 则的长为 .
三、解答题
-
14.(1)、分解因式: .(2)、解不等式组: , 并求出不等式组的整数解.15. 解分式方程: .16. 如图所示,在平面直角坐标系中,每个小方格都是边长为1个单位长度的正方形,的顶点均在格点上.

⑴将先向下平移4个单位长度,再向左平移2个单位长度,得到 , 请画出;
⑵将绕着点逆时针旋转 , 画出旋转后得到的 , 并直接写出的坐标;
⑶连接 , 求线段的长.
17. 如图,在四边形中, , , 为边上一点,连接 , 相交于点F,且 , 连接 . (1)、求证:四边形是平行四边形;(2)、取中点 , 连接 , 若 , , , 求四边形的面积.18. 关于直线( , 为常数,且)和有如下信息:
(1)、求证:四边形是平行四边形;(2)、取中点 , 连接 , 若 , , , 求四边形的面积.18. 关于直线( , 为常数,且)和有如下信息:①当时,;当时,;
②当时, .
(1)、求直线的函数关系式;(2)、在图中画出 , 的图象;(3)、若 , 求出 , , 围成的图形的面积.四、填空题
-
19. 若多项式分解因式后的结果为 , 则的值为 .20. 已知 , 则代数式的值为 .21. 现定义一种新运算: , 若满足 , 则的取值范围为 .22. 如图,点E,F分别为的边的中点, , , , 则 .
 23. 如图,在等腰中, , , 于点 , 点M,N分别是DE,DG上的动点,且 , 则的最小值为 .
23. 如图,在等腰中, , , 于点 , 点M,N分别是DE,DG上的动点,且 , 则的最小值为 .
五、解答题
-
24. 为了做好今年的防汛工作,确保人民群众生命财产安全,某地计划对区域内的河道清淤疏浚,提高河道行洪、排涝能力.现打算租赁A、B两种型号的卡车转运河道内淤积的泥沙,已知A、B两种型号卡车的相关信息如下表所示:
车辆型号
A型
B型
运输量(吨/辆・天)
租金(元/辆・天)
1000
800
若A型卡车每天转运3000吨泥沙与B型卡车每天转运2700吨泥沙所需车辆数相同.
(1)、求出上表中的值(写出解题过程);(2)、该地计划租赁A、B两种型号的卡车共10辆,且满足每天转运的泥沙不少于4750吨,租金总额不超过9600元.①若设租赁A型卡车辆,每天的租金总额为元,请写出与的关系式;
②请列出所有的租赁方案,并求出最节省的租赁方案和此时的租金总额.
25. 如图,在边长为的正方形纸片中剪去一个边长为的小正方形纸片 , 把剩余的部分拼成一个长方形纸片. (1)、通过计算两个纸片中阴影部分的面积,可得等式____(填选项前面的字母);A、 B、 C、 D、(2)、请利用(1)中所选的结论,解答以下问题:
(1)、通过计算两个纸片中阴影部分的面积,可得等式____(填选项前面的字母);A、 B、 C、 D、(2)、请利用(1)中所选的结论,解答以下问题:①如图,大正方形ABCD的面积为 , 小正方形的面积为 , 且 , 求不规则四边形的面积;

②计算: .
26. 如图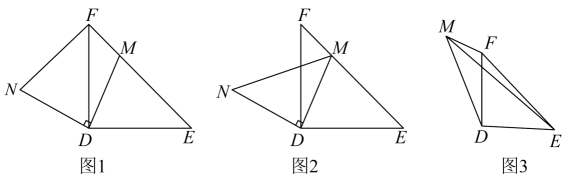 (1)、尝试解决:如图1,在中, , , 点M在边上运动(M不与点E,F重合),连接 , 过点D作线段 , 垂足为点D,且 , 连接 , 求出的度数;(2)、类比探究:如图2,在中, , , 点M在边上运动(M不与点E,F重合),连接 , 以为腰在上方作等腰 , 其中 , , 试问线段之间有怎样的等量关系?写出结论并证明;(3)、拓展应用:如图3,在中, , , 在左侧作 , 若 , , 求出的长度.
(1)、尝试解决:如图1,在中, , , 点M在边上运动(M不与点E,F重合),连接 , 过点D作线段 , 垂足为点D,且 , 连接 , 求出的度数;(2)、类比探究:如图2,在中, , , 点M在边上运动(M不与点E,F重合),连接 , 以为腰在上方作等腰 , 其中 , , 试问线段之间有怎样的等量关系?写出结论并证明;(3)、拓展应用:如图3,在中, , , 在左侧作 , 若 , , 求出的长度.