四川省达州市宣汉县2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-29 类型:期末考试
一、单选题
-
1. 不等式3x<-6的解集是( )A、x>-2 B、x<-2 C、x≥-2 D、x≤-22. 在以下”绿色食品、响应环保、可回收物、节水“四个标志图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 一元一次不等式组 的解集在数轴上表示为( ).A、
3. 一元一次不等式组 的解集在数轴上表示为( ).A、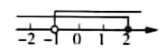 B、
B、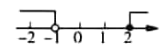 C、
C、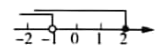 D、
D、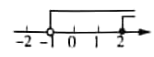 4. 若分式的值为零,则的值为( )A、 B、 C、 D、5. 把代数式2x2﹣18分解因式,结果正确的是( )A、2(x2﹣9) B、2(x﹣3)2 C、2(x+3)(x﹣3) D、2(x+9)(x﹣9)6. 在平面直角坐标系中,若直线y=2x+k经过第一、二、三象限,则k的取值范围是( )A、k>0 B、k<0 C、k≤0 D、k≥07. 某农场开挖一条长480米的渠道,开工后每天比原计划多挖20米,结果提前4天完成任务,若设原计划每天挖x米,那么下列方程中正确的是( )A、 B、 C、 D、8. 若关于x的方程 + =3的解为正数,则m的取值范围是( )
4. 若分式的值为零,则的值为( )A、 B、 C、 D、5. 把代数式2x2﹣18分解因式,结果正确的是( )A、2(x2﹣9) B、2(x﹣3)2 C、2(x+3)(x﹣3) D、2(x+9)(x﹣9)6. 在平面直角坐标系中,若直线y=2x+k经过第一、二、三象限,则k的取值范围是( )A、k>0 B、k<0 C、k≤0 D、k≥07. 某农场开挖一条长480米的渠道,开工后每天比原计划多挖20米,结果提前4天完成任务,若设原计划每天挖x米,那么下列方程中正确的是( )A、 B、 C、 D、8. 若关于x的方程 + =3的解为正数,则m的取值范围是( )
A、m< B、m< 且m≠ C、m>﹣ D、m>﹣ 且m≠﹣9. 如图,的周长是24,点D、E在边上,的平分线垂直于 , 垂足为点Q,的平分线垂直于 , 垂足为点P,若 , 则的长为( ) A、5 B、4 C、2 D、310. 在平面直角坐标系中,长为的线段点在点的右侧在轴上移动,轴上的点、坐标分别为 , 、 , , 连接 , , 则的最小值为( )
A、5 B、4 C、2 D、310. 在平面直角坐标系中,长为的线段点在点的右侧在轴上移动,轴上的点、坐标分别为 , 、 , , 连接 , , 则的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 正n边形的一个外角的度数为60°,则n的值为 .12. 在等腰中, , , 则 .13. 如图,函数y=2x和y=ax+4的图象相交于点A( , 3),则不等式2x>ax+4的解集为.
 14. 已知关于 的不等式组 有四个整数解,则实数 的取值范围为.15. 如图所示,在锐角中,分别以和为斜边向外侧作等腰和等腰 , 点D、E、F分别为边、、的中点,连接、、、、、 . 则下列结论:①四边形是平行四边形;②;③;④ , 其中正确结论的序号是 .
14. 已知关于 的不等式组 有四个整数解,则实数 的取值范围为.15. 如图所示,在锐角中,分别以和为斜边向外侧作等腰和等腰 , 点D、E、F分别为边、、的中点,连接、、、、、 . 则下列结论:①四边形是平行四边形;②;③;④ , 其中正确结论的序号是 .
三、解答题
-
16. 解分式方程:17. 解不等式组:并在数轴上表示出它的解集.
 18. 化简: , 并从中选取一个合适的整数代入求值.19. 在平面直角坐标系中,的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
18. 化简: , 并从中选取一个合适的整数代入求值.19. 在平面直角坐标系中,的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
⑴将沿y轴方向向下平移4个单位长度得到 , 画出并直接写出点坐标;
⑵将绕着点O逆时针旋转 , 画出旋转后得到的;
⑶直接写出点 , 的坐标.
20. 如图,在中, , 是高,是的外角的平分线. (1)、用尺规作图方法,作的平分线保留作图痕迹,不写作法和证明);(2)、设与交于点 , 判断的形状,并说明理由.21. 如图,在中,平分交延长线于点E,作 , 垂足为点F.
(1)、用尺规作图方法,作的平分线保留作图痕迹,不写作法和证明);(2)、设与交于点 , 判断的形状,并说明理由.21. 如图,在中,平分交延长线于点E,作 , 垂足为点F. (1)、求证:;(2)、若 , , 求的周长.22. 东东玩具商店用500元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用900元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)、求证:;(2)、若 , , 求的周长.22. 东东玩具商店用500元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用900元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)、求第一批悠悠球每套的进价是多少元;(2)、如果这两批悠悠球每套售价相同,且全部售完后总利润不低于25%,那么每套悠悠球的售价至少是多少元?
23. 某学校计划组织全校1500名师生外出参加集体活动,经过研究,决定租用当地租车公司一共60辆A、B两种型号客车作为交通工具.下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号
载客量
租金单价
A
30人/辆
400元/辆
B
20人/辆
300元/辆
注:载客量是指不包括驾驶员的每辆客车最多载客人数.学校租用A型号客车x辆,租车总费用为y元.
(1)、求y与x的函数解析式,并直接写出x的取值范围;(2)、若要使租车总费用不超过22000元,一共有几种租车方案?并结合函数性质说明哪种租车方案最省钱?最低费用是多少元?24. 我们把多项式及叫做完全平方式.如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些非负数有关的问题或求代数式最大值、最小值等.例如:分解因式;例如求代数式的最小值.由可知,当时,有最小值,最小值是 .
根据阅读材料用配方法解决下列问题;
(1)、分解因式:;(2)、当a,b为何值时,多项式有最小值,并求出这个最小值;(3)、当a,b为何值时,多项式有最小值,并求出这个最小值.25. 如图,在平面直角坐标系中,已知直线交x轴于点A,交y轴于点 , 过点C作直线交x轴于点B,且 , , 点P在线段上,P的坐标为 . (1)、求的长;(2)、若M为线段的中点,求直线的解析式;(3)、在平面内是否存在点Q,使以点A、C、P、Q为顶点的四边形是平行四边形?若存在请直接写出点Q的坐标;若不存在请说明理由.
(1)、求的长;(2)、若M为线段的中点,求直线的解析式;(3)、在平面内是否存在点Q,使以点A、C、P、Q为顶点的四边形是平行四边形?若存在请直接写出点Q的坐标;若不存在请说明理由.