四川省广安市岳池县2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-29 类型:期末考试
一、单选题
-
1. 已知菱形的周长与其边长的函数关系式为 , 其中是( )A、函数 B、函数值 C、常量 D、自变量2. 若式子在实数范围内有意义,则a的取值范围是( )A、 B、 C、 D、3. 一个直角三角形的两条直角边分别长3和4,则斜边的长为( )A、 B、5 C、或5 D、5或74. 下列性质中,平行四边形一定具备的是( )A、邻角互补 B、四边相等 C、有一个角是直角 D、对角线相等5. 某场比赛,共有10位评委分别给出某选手的原始评分,评定该选手的成绩时,从10个原始评分中去掉一个最高分、一个最低分,得到8个有效评分,8个有效评分与10个原始评分相比,一定不变的数据特征是( )A、平均数 B、众数 C、中位数 D、方差6. 下列计算正确的是( )A、 B、 C、 D、7. 正比例函数y=kx(k≠0)的图象在第二、四象限,则一次函数y=x+k的图象大致是( )A、
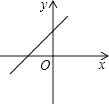 B、
B、 C、
C、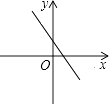 D、
D、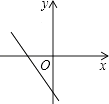 8. 如图,在中, , 分别以斜边、直角边为边作正方形和正方形 . 若正方形的面积为36, , 则正方形的面积为( )
8. 如图,在中, , 分别以斜边、直角边为边作正方形和正方形 . 若正方形的面积为36, , 则正方形的面积为( ) A、 B、11 C、 D、319. 如图,在中, , 分别是 , 的中点,是上一点, . 若 , , 则的长为( )
A、 B、11 C、 D、319. 如图,在中, , 分别是 , 的中点,是上一点, . 若 , , 则的长为( ) A、 B、 C、 D、10. 已知 , 两地相距4千米.上午8:00,甲从地出发步行到地,8:20乙从地出发骑自行车到地.甲、乙两人离地的距离(千米)与甲所用的时间(分)之间的关系如图所示.由图中的信息可知,乙的平均速度是( )
A、 B、 C、 D、10. 已知 , 两地相距4千米.上午8:00,甲从地出发步行到地,8:20乙从地出发骑自行车到地.甲、乙两人离地的距离(千米)与甲所用的时间(分)之间的关系如图所示.由图中的信息可知,乙的平均速度是( ) A、9千米/时 B、10千米/时 C、11千米/时 D、12千米/时
A、9千米/时 B、10千米/时 C、11千米/时 D、12千米/时二、填空题
-
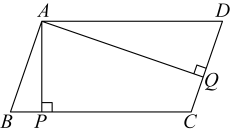
11. 如图,在平行四边形中,于点 , 于点 , 则直线与间的距离是线段的长度.(填图中已有线段)
 12. 广安邓小平故里是全国重点文物保护单位、全国红色旅游经典景区.该景区计划招聘一名工作人员,面试官从内容、文化两个方面为应聘者打分,按内容占40%、文化占60%计算应聘者的综合分.已知应聘者小李的内容、文化的得分分别为80分、90分,则他的综合分是分.13. 如图,直线与相交于点 , 则关于的方程的解是 .
12. 广安邓小平故里是全国重点文物保护单位、全国红色旅游经典景区.该景区计划招聘一名工作人员,面试官从内容、文化两个方面为应聘者打分,按内容占40%、文化占60%计算应聘者的综合分.已知应聘者小李的内容、文化的得分分别为80分、90分,则他的综合分是分.13. 如图,直线与相交于点 , 则关于的方程的解是 . 14. 若最简二次根式与最简二次根式是同类二次根式,则 .15. 在中, , , 的对边分别是 , , , 下列条件:①与互余;②;③ , 其中可以判定是直角三角形的有个.16. 古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所得两长方形面积相等”(如图1),问题解决:如图2,点P是矩形的对角线上一点,过点P作分别交 , 于点E,F,连接 , . 若 , , 则图中阴影部分的面积和为 .
14. 若最简二次根式与最简二次根式是同类二次根式,则 .15. 在中, , , 的对边分别是 , , , 下列条件:①与互余;②;③ , 其中可以判定是直角三角形的有个.16. 古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所得两长方形面积相等”(如图1),问题解决:如图2,点P是矩形的对角线上一点,过点P作分别交 , 于点E,F,连接 , . 若 , , 则图中阴影部分的面积和为 .
三、解答题
-
17. 先化简,再求值: , 其中 .18. 在如图所示的方格纸上,以格点为顶点,按要求画图.
 (1)、在图1中画一个直角三角形,要求:三角形的三边长是勾股数;(2)、在图2中画一个菱形,要求:线段为菱形的对角线.19. 如图,在平面直角坐标系中,正比例函数的图像经过点 , 一次函数的图像经过点 , .
(1)、在图1中画一个直角三角形,要求:三角形的三边长是勾股数;(2)、在图2中画一个菱形,要求:线段为菱形的对角线.19. 如图,在平面直角坐标系中,正比例函数的图像经过点 , 一次函数的图像经过点 , . (1)、求一次函数的解析式;(2)、在图中画出一次函数的图像;(3)、根据函数图象,直接写出当时,自变量的取值范围.20. 如图,菱形的对角线 , 相交于点 , 在上截取 , 顺次连接 , , , 四点.求证:四边形是正方形,
(1)、求一次函数的解析式;(2)、在图中画出一次函数的图像;(3)、根据函数图象,直接写出当时,自变量的取值范围.20. 如图,菱形的对角线 , 相交于点 , 在上截取 , 顺次连接 , , , 四点.求证:四边形是正方形, 21. 图1是某品牌婴儿车,图2为其简化结构示意图.根据安全标准需满足 , 现测得dm,dm,dm,其中与之间由一个固定为90°的零件连接(即),通过计算说明该车是否符合安全标准.
21. 图1是某品牌婴儿车,图2为其简化结构示意图.根据安全标准需满足 , 现测得dm,dm,dm,其中与之间由一个固定为90°的零件连接(即),通过计算说明该车是否符合安全标准. 22. 如图,木工师傅在一块矩形木料上截出两块面积分别为和的正方形木板.
22. 如图,木工师傅在一块矩形木料上截出两块面积分别为和的正方形木板.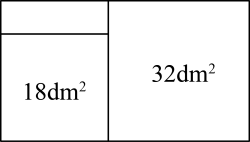 (1)、截出的两块正方形木板中,小正方形木板的边长为dm,大正方形木板的边长为dm;(填最简二次根式)(2)、求原矩形木料的面积;(3)、木工师傅想从剩余矩形木料中截出一块正方形木板,这块正方形木板的边长为2dm.(填“能”或“不能”)23. 教育部印发《2023年全国综合防控儿童青少年近视重点工作计划》,全面部署年度全国综合防控儿童青少年近视重点工作计划.为提高学生对保护视力的重视程度,某校组织了关于近视防控知识的专题讲座,并进行了相关知识测评.现从该校八、九年级中各随机抽取10名学生的测试成绩(百分制)进行整理和分析(成绩得分用x表示,共分成四组:A. , B. , C. , D.).下面给出了部分信息:
(1)、截出的两块正方形木板中,小正方形木板的边长为dm,大正方形木板的边长为dm;(填最简二次根式)(2)、求原矩形木料的面积;(3)、木工师傅想从剩余矩形木料中截出一块正方形木板,这块正方形木板的边长为2dm.(填“能”或“不能”)23. 教育部印发《2023年全国综合防控儿童青少年近视重点工作计划》,全面部署年度全国综合防控儿童青少年近视重点工作计划.为提高学生对保护视力的重视程度,某校组织了关于近视防控知识的专题讲座,并进行了相关知识测评.现从该校八、九年级中各随机抽取10名学生的测试成绩(百分制)进行整理和分析(成绩得分用x表示,共分成四组:A. , B. , C. , D.).下面给出了部分信息:八年级10名学生的测试成绩是:91,92,80,80,80,71,70,75,70,91.
九年级10名学生的测试成绩在C组中的数据是:82,84,84,89.
八、九年级抽取的学生测试成绩分析统计表
年级
平均数
中位数
众数
方差
八年级
80
80
九年级
83
84
九年级抽取的学生测试成绩统计图

根据上述信息,解答下列问题:
(1)、统计表中, , ;(2)、求抽取的八年级10名学生的测试成绩的方差的值;(3)、估计该校八、九年级学生中,年级学生的测试成绩更为稳定.24. 甲、乙两家水果店平时以同样的价格出售品质相同的广安华蓥樱桃.假期间,甲、乙两家水果店都让利酬宾,甲店的樱桃的原价为30元/kg,现打九折;乙店的樱桃的价格为30元/kg,现一次购买2kg以上,超过2kg的部分打八折.顾客到甲、乙两家水果店购买樱桃的付款金额 , (元)与购买樱桃的质量之间的关系如图所示. (1)、求 , 关于的函数解析式;(2)、两图象交于点 , 求点的坐标,并说明其实际意义;(3)、请根据函数图象,分情况说明选择去哪家水果店购买樱桃更合算.
(1)、求 , 关于的函数解析式;(2)、两图象交于点 , 求点的坐标,并说明其实际意义;(3)、请根据函数图象,分情况说明选择去哪家水果店购买樱桃更合算.
