四川省广元市朝天区2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-29 类型：期末考试

进入出卷网下载

一、单选题

1. 在圆的周长公式 $C = 2 π r$ 中，常量是（）

A、 $C$ B、2 C、 $r$ D、 $2 π$

查看试题解析
2. 若3，4，a是一组勾股数，则a的值为（）

A、 $\sqrt{7}$ B、5 C、 $\sqrt{7}$ 或5 D、6

查看试题解析
3. 如图，平行四边形 $A B C D$ 的顶点 $C$ 在直线 $M N$ 上．若 $∠ 1 = 50 °$ ， $∠ 2 = 20 °$ ，则 $∠ A$ 的度数为（）

A、 $80 °$ B、 $110 °$ C、 $130 °$ D、 $150 °$

查看试题解析
4. 下列运算正确的是（）

A、 $2 + \sqrt{2} = 2 \sqrt{2}$ B、 $\sqrt{24} \times \sqrt{\frac{1}{3}} = 8$ C、 $\sqrt{32} \div \sqrt{8} = 2$ D、 $\sqrt{0.4 a^{3}} = 0.2 a (a > 0)$

查看试题解析
5. 在一次演讲比赛中，某位选手的演讲内容、演讲表达的得分分别为95分，90分，将演讲内容、演讲表达的成绩按 $6 ： 4$ 计算，则该选手的成绩是（）

A、94分 B、93分 C、92分 D、91分

查看试题解析
6. 如图，在数轴上，以 $- 1$ 所在点 $A$ 为圆心 $A B$ 的长为半径画弧，交数轴正半轴于点 $C$ ，则点 $C$ 对应的实数是（）

A、 $\sqrt{5}$ B、 $1 + \sqrt{5}$ C、 $- 1 + \sqrt{5}$ D、 $- 1 - \sqrt{5}$

查看试题解析
7. 如图，在正方形 $A B C D$ 的外侧作等边三角形 $A D E$ ，则 $∠ A E B$ 度数为（）

A、 $10 °$ B、 $15 °$ C、 $22.5 °$ D、 $30 °$

查看试题解析
8. 如图，四边形ABCD是平行四边形，下列结论中错误的是（）

A、当▱ABCD是矩形时，∠ABC＝90° B、当▱ABCD是菱形时，AC⊥BD C、当▱ABCD是正方形时，AC＝BD D、当▱ABCD是菱形时，AB＝AC

查看试题解析
9. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A B C = 60 °$ ， $B D$ 平分 $∠ A B C$ 交 $A C$ 于点 $D$ ， $P$ 是 $B D$ 的中点，连接 $C P$ ．若 $C P = 4$ ，则 $A D$ 的长为（）

A、8 B、6 C、10 D、9

查看试题解析
10. A、B两地相距12km，甲骑自行车从A地出发前往B地，同时乙步行从B地出发前往A地，如图所示的折线 $O - P - Q$ 和线段EF分别表示甲、乙两人与A地的距离y（km）与时间x（h）之间的函数关系，且OP与EF交于点G．下列说法中错误的是（）

A、甲乙出发后0.5h相遇 B、甲骑自行车的速度为 $18 k m / h$ C、两人相遇地点与A地的距离为9km D、甲、乙相距3km时，出发时间为 $x = \frac{3}{5} h$

查看试题解析

二、填空题

11. 若代数式 $\sqrt{6 - 3 x}$ 在实数范围内有意义，则x的取值范围是.

查看试题解析
12. 去年某果园随机从甲、乙、丙三个品种的枇杷树中各选了25棵，每棵枇杷树产量（单位： $k g$ ）的平均数 $x$ 及方差 $s^{2}$ 如下表所示：
品种
甲
乙
丙
          $x$
42
45
45
          $s^{2}$
1.8
23
1.8
今年准备从这三个品种中选出一种产量既高又稳定的枇杷树进行种植，则应选的品种是．（填“甲”“乙”或“丙”）

查看试题解析
13. 若一次函数 $y = - \frac{1}{2} x + b$ 的图象经过点 $(0 ， y_{1})$ ， $(x_{2} ， y_{2})$ ，当 $x_{2} > 0$ 时， $y_{1}$ 与 $y_{2}$ 的大小关系是 $y_{1}$ $y_{2}$ ．（填“>”或“<”）

查看试题解析
14. 把图1中的菱形沿对角线分成四个全等的直角三角形，将这四个直角三角形分别拼成如图2，图3所示的正方形，则图1中菱形的面积为．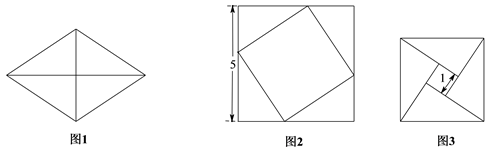

查看试题解析
15. 阅读材料：希腊几何学家海伦和我国南宋数学家秦九韶曾提出利用三角形的三边求面积的公式，称为海伦—秦九韶公式：如果一个三角形的三边长分别是 $a$ ， $b$ ， $c$ ，记 $p = \frac{a + b + c}{2}$ ，那么三角形的面积为 $S = \sqrt{p (p - a) (p - b) (p - c)}$ ．如图，在 $△ A B C$ 中， $a = 7$ ， $b = 5$ ， $c = 6$ ，则 $B C$ 边上的高为．

查看试题解析
16. 如图，点 $B$ ， $C$ 分别在正比例函数 $y = 2 x$ 和一次函数 $y = k x - 2 a (a \neq 0)$ 的图象上， $A$ ， $D$ 为 $x$ 轴上两点，点 $B$ 的纵坐标为 $a$ ．若四边形 $A B C D$ 为矩形，且 $A B = \frac{1}{2} A D$ ，则 $k$ 的值为．

查看试题解析

三、解答题

17. 计算： $\sqrt{20} - \sqrt{30} \div \sqrt{6} + (2 - \sqrt{3}) (2 + \sqrt{3})$ ．

查看试题解析
18. 如图所示的 $6 \times 6$ 方格纸上每个小正方形的边长都为1．在方格纸上按要求画图．

(1)、在图1中以点 $A$ 为顶点，画边长为 $\sqrt{2}$ ， $\sqrt{5}$ ， $\sqrt{5}$ 的 $△ A B C$ ；

(2)、在图2中以 $A B$ 为一边，画菱形 $A B C D$ ．

查看试题解析
19. 如图， $E$ 是平行四边形 $A B C D$ 中边 $A D$ 延长线的上一点，连接 $B E$ ， $C E$ ， $B D$ ．若 $∠ A B D = ∠ D C E$ ，求证：四边形 $B C E D$ 为平行四边形．

查看试题解析
20. 已知 $△ A B C$ 的三边长分别为 $a$ ， $b$ ， $c$ ．

(1)、化简： $\sqrt{(a - b - c)^{2}}$ ；

(2)、若 $a$ ， $b$ 满足 $b = \sqrt{5 - a} + \sqrt{a - 5} + 13$ ，且 $c = 12$ ，判断此三角形的形状，并说明理由．

查看试题解析
21. 如图， $A$ ， $B$ 是 $x$ 轴上分别位于原点左、右两侧的点，点 $P (2 ， a)$ 在第一象限内，直线 $P A ： y = k x + b$ 交 $y$ 轴于点 $C (0 ， 2)$ ，直线 $P B$ 的函数解析式为 $y = m x + n$ ，且 $S_{△ A O P} = 12$ ．

(1)、求直线 $P A$ 的函数解析式和 $a$ 的值；

(2)、直接写出关于 $x$ 的不等式 $m x + n \leq k x + b$ 的解集．

查看试题解析

22. 争创全国文明城市——从我做起．某中学开设了文明礼仪校本课程，为了解学生的学习情况，学校组织七、八年级学生进行文明礼仪知识测试，从七、八年级中各随机抽取了10名学生的测试成绩（满分100分），整理分析如下：

七年级： $99$ ， $98$ ， $98$ ， $98$ ， $95$ ， $93$ ， $91$ ， $90$ ， $89$ ， $79$ ；

八年级： $99$ ， $99$ ， $99$ ， $91$ ， $96$ ， $90$ ， $93$ ， $87$ ， $91$ ， $85$ ．

整理分析上面的数据，得到如下表格：

统计量	平均数	中位数	众数	方差
七年级	$93$	$94$	$a$	$34$
八年级	$93$	$b$	$99$	$c$

根据以上信息，解答下列问题．

(1)、统计表中

a =

，

b =

；

(2)、若在收集七年级数据的过程中将抽取的

“ 89 ”

误写成了

“ 79 ”

，则七年级数据的平均数、中位数、众数中将发生变化的是；

(3)、计算八年级测试成绩的方差

c

，并根据统计结果，说明哪个年级的测试成绩更稳定．

查看试题解析

23. 如图，在菱形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点 $O$ ，延长 $C B$ 到点 $E$ ，使得 $B E = B C$ ．连接 $A E$ ．过点 $B$ 作 $B F ∥ A C$ ，交 $A E$ 于点 $F$ ，连接 $O F$ ．

(1)、求证：四边形 $A F B O$ 是矩形；

(2)、若 $∠ E = 30 °$ ， $B F = 1$ ，求 $O F$ 的长．

查看试题解析
24. 如图，某游乐场的游客中心位于 $A$ 处，其正南方向 $600 m$ 处有海盗船游乐项目 $B$ ，在海盗船游乐项目 $B$ 的正东方向 $800 m$ 处是摩天轮游乐项目 $C$ ，餐厅 $D$ 位于 $A C$ 的中点处；碰碰车游乐项目 $F$ 位于 $B C$ 的中点处．小乐和曼曼同时从 $A$ 处出发，小乐经 $B$ 处到 $C$ 处匀速游玩，曼曼先沿 $A D$ 路线匀速游玩到餐厅 $D$ ，后又沿南偏西方向的 $D E$ 路线匀速直线游玩．曼曼全程与小乐的游玩速度相同．

(1)、餐厅 $D$ 和碰碰车游乐项目 $F$ 的距离是 $m$ ；

(2)、若小乐在由 $B$ 到 $C$ 游玩途中与曼曼相遇于 $E$ 处，求相遇处 $E$ 到海盗船游乐项目 $B$ 的距离．

查看试题解析
25. 为落实“双减”政策，丰富课后服务的内容，某校计划到甲、乙两个体育专卖店购买一批新的体育用品，甲、乙两个体育专卖店的优惠活动如下：
甲：所有商品按原价的8.5折出售．
乙：一次性购买商品总额不超过300元的按原价付；超过300元的部分打7折．
在两家商店购买的实付款 $y_{甲}$ ， $y_{乙}$ （单位：元）与商品原价 $x$ （单位：元）之间的关系如图所示．

(1)、分别求出实付款 $y_{甲}$ ， $y_{乙}$ 与商品原价 $x$ 之间的函数关系式；

(2)、已知两图象交于点A，求点A的坐标，并说明其实际意义；

(3)、请根据函数图象，直接写出选择去哪个体育专卖店购买体育用品更合算．

查看试题解析
26. 四边形ABCD为正方形，点E为线段AC上一点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG.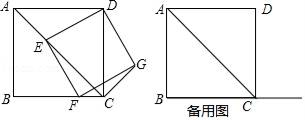

(1)、如图1，求证：矩形DEFG是正方形；

(2)、若AB=2，CE= $\sqrt{2}$ ，求CG的长度；

(3)、当线段DE与正方形ABCD的某条边的夹角是30°时，直接写出∠EFC的度数.

查看试题解析

品种	甲	乙	丙
$x$	42	45	45
$s^{2}$	1.8	23	1.8