（单元测试A卷）第四章 等可能条件下的概率—苏科版2023-2024学年九年级数学上册
试卷更新日期：2023-08-28 类型：单元试卷
一、选择题（每题3分，共30分）
-
1. 下列事件中，属于必然事件的是（ ）A、射击运动员射击一次，命中10 环 B、有一匹马奔跑的速度是70米/秒 C、任意抛掷一只纸杯，杯口朝下 D、在地面上向空中抛掷一石块，石块终将落下2. 下列事件中是不可能事件的是（ ）A、连续3天下雨 B、三角形的外心到三角形三个顶点的距离相等 C、任意多边形外角和都是 D、买彩票中奖3. 掷一枚质地均匀的标有1，2，3，4，5，6六个数字的立方体骰子，骰子停止后，出现可能性最小的是（ ）A、大于3的点数 B、小于3的点数 C、大于5的点数 D、小于5的点数4. 一个布袋里装有5个球，其中3个红球，2个白球，每个球除颜色外其余都相同，则从布袋里任意摸出一个球是红球的概率是（ ）A、 B、 C、 D、5. 一个不透明的袋中装有9个只有颜色不同的球，其中3个红球，5个白球和1个黄球，从中任意摸出一个球是白球的概率是（ ）A、 B、 C、 D、6. 书架上有1本数学书，2本物理书．从中任取1本书是物理书的概率为（ ）A、 B、 C、 D、7. 一个不透明布袋里有四个完全相同的小球，把它们分别标号为1，2，3，5，从中任意摸出一个球，记下编号后放回，搅匀，再任意摸出一个球，则两次摸出的球的编号之和为偶数的概率是（ ）A、 B、 C、 D、8. 下列说法错误的是（ ）A、同时抛两枚普通正方体骰子，点数都是4的概率为 B、不可能事件发生的概率为0 C、买一张彩票会中奖是随机事件 D、一件事发生机会为1.0%，这件事就有可能发生9. 如图，同时转动两个转盘，转盘的指针同时在红色区域内的概率为（ ）
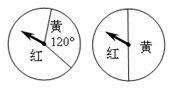A、 B、 C、 D、10. 如图，直径AB、CD互相垂直，现有一小球在此圆盘上滚动，落在阴影部分的概率为（ ）
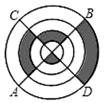A、 B、 C、 D、二、填空题（每空3分，共15分）
-
11. 在一个箱子里放有2个白球和5个红球，现摸出1个球是黑球，这个事件属于事件（填“必然，不确定或不可能”）12. 任意抛掷一枚均匀的骰子，骰子各个面的点数分别为1，2，3，4，5，6，则朝上的点数是奇数的概率是13. 在一个不透明的口袋中有五个完全相同的小球，把它们分别标号为1，2，3，4，5.若随机摸出一个小球，小球上的数字小于3的概率为.14. 如图是由8块全等的等腰直角三角形黑白瓷砖镶嵌而成的正方形，一只蚂蚁在上面自由爬动，那么蚂蚁停留在黑色瓷砖上的概率是.
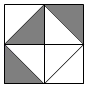15. 如果小球在如图所示的地板上自由地滚动，并随机停留在某块方砖上，那么小球最终停留在黑色区域的概率是 ．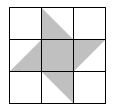
三、解答题（共4题，共20分）
-
16. 在不透明的袋子中装有3个红球和5个黄球，每个球除颜色外都相同，从中任意摸出一个球
（1）摸到哪种颜色球的可能性大？
（2）请你通过改变袋子中某一种颜色球的数量，设计一种方案；使“摸出红球”和“摸出黄球”的可能性大小相同．
17. “共和国勋章”是中华人民共和国的最高荣誉勋章.在2019年获得“共和国勋章”的八位杰出人物中，有于敏、孙家栋、袁隆平、黄旭华四位院士.如图是四位院士（依次记为A，B，C，D）为让同学们了解四位院士的贡献，老师设计如下活动：取四张完全相同的卡片，分别写上A，B，C，D四个标号，然后背面朝上放置，搅匀后每个同学可从中随机抽取一张，记下标号后放回，老师要求每位同学根据抽到的卡片上的标号查找相应院士的资料制作小报，求小明和小华查找同一位院士资料的概率.A．
B． 
C． 
D． 
18. 有3张不透明的卡片，分别标号为A、B、C，它们除正面上的图案不同外，其他均相同．将这3张卡片背面向上洗匀后放在桌面上．若从中随机抽取1张卡片，记下标号后放回洗匀，再随机抽取1张记下标号，请用画树状图或列表的方法求两次所抽取的卡片恰好都是中心对称图形的概率．
19. 为落实“十个一”活动，学校组建了多个志愿者服务队，小盖和小吕通过做游戏决定谁优先选择服务队，游戏规则：两人各掷一次质地均匀的骰子，如果掷出的点数之和是小于7的偶数，由小盖优先选择服务队；如果掷出的点数之和是大于6的奇数，由小吕优先选择服务队，请利用画树状图或列表的方法，判断这个游戏对双方是否公平．四、综合题（共4题，共35分）
-
20. 有一个转盘（如图所示），被分成6个相等的扇形，颜色分为红、绿、黄三种，指针的位置固定，转动转盘后任其自由停止，其中的某个扇形会恰好停在指针所指的位置（指针指向两个扇形的交线时，重新转动）．下列事件：①指针指向红色；②指针指向绿色；③指针指向黄色；④指针不指向黄色．估计各事件的可能性大小，完成下列问题：
(1)、可能性最大和最小的事件分别是哪个？（填写序号）
(2)、将这些事件的序号按发生的可能性从小到大的顺序排列： ．
21. 某节能灯厂出售一批额定功率为的节能灯，每盒装有100个节能灯，由于包装工人的疏忽，在包装时混进了额定功率的节能灯.某批发商从工厂购进了50盒的节能灯，每盒中混入灯数如表：每盒中混入灯数（个）
0
1
2
3
4
盒数
14
25
9
1
1
(1)、平均每盒混入几个灯？(2)、若一盒混入节能灯的数量大于 ， 工厂需给批发商赔偿.从这50盒中任意抽取一盒，记事件A为：该盒需要给批发商赔偿.求事件A的概率.22. 为坚持“五育并举”，落实立德树人根本任务，教育部出台了“五项管理”举措．我校对九年级部分家长就“五项管理”知晓情况作调查，A：完全知晓，B：知晓，C：基本知晓，D：不知晓．九年级年级组长将调查情况制成了条形统计图和扇形统计图．请根据图中信息，回答下列问题：
(1)、共调查了名家长；图2中D选项所对应的圆心角度数为；(2)、已知D选项中男女家长数相同，若从D选项家长中随机抽取2名家长参加“家校共育”座谈会，请用列表或画树状图的方法，求抽取家长恰好是一男一女的概率．23. 一个不透明的口袋中有三个完全相同的小球，把它们分别标号为1，2，3．甲从口袋中随机摸取一个小球，记下标号m，然后放回，再由乙从口袋中随机摸取一个小球，记下标号n，组成一个数对（m，n）．(1)、用列表法或画树状图法，写出（m，n）所有可能出现的结果；(2)、甲、乙两人玩游戏，规则如下：按上述要求，两人各摸取一个小球，小球上标号之和为奇数则甲赢，小球上标号之和为偶数则乙赢．你认为这个游戏规则公平吗？请说明理由．