四川省内江市2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-28 类型:期末考试
一、单选题
-
1. 下列各式: , 分式有( )A、1个 B、2个 C、3个 D、4个2. 某种秋冬流感病毒的直径约为0.000000203米,该直径用科学记数法表示为( )米.A、2.03×10﹣8 B、2.03×10﹣7 C、2.03×10﹣6 D、0.203×10﹣63. 在函数 中,自变量 的取值范围是( )A、 B、 C、 且 D、4. 已知: ﹣ = ,则 的值是( )A、 B、﹣ C、3 D、﹣35. 下列曲线中不能表示y是x的函数的是( )A、
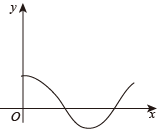 B、
B、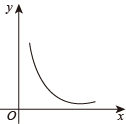 C、
C、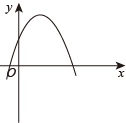 D、
D、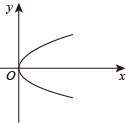 6. 在一次献爱心的捐款活动中,八(2)班50名同学捐款金额如图所示,则在这次捐款活动中,该班同学捐款金额的众数和中位数分别是( )
6. 在一次献爱心的捐款活动中,八(2)班50名同学捐款金额如图所示,则在这次捐款活动中,该班同学捐款金额的众数和中位数分别是( )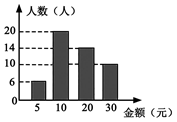 A、20,10 B、10,20 C、10,10 D、10,157. 如图,在矩形中, , 点M在边上,若平分 , 则的长是( )
A、20,10 B、10,20 C、10,10 D、10,157. 如图,在矩形中, , 点M在边上,若平分 , 则的长是( ) A、 B、 C、 D、8. 若关于x的分式方程 产生增根,则m的值为( )A、 B、 C、1 D、29. 下列判断正确的是( )A、对角线互相垂直的四边形是菱形 B、对角线相等的菱形是正方形 C、对角线相等的四边形是矩形 D、对角线互相垂直且相等的四边形是正方形10. 下列图形中,能表示一次函数与正比例函数(m、n为常数)的图象的是( )A、
A、 B、 C、 D、8. 若关于x的分式方程 产生增根,则m的值为( )A、 B、 C、1 D、29. 下列判断正确的是( )A、对角线互相垂直的四边形是菱形 B、对角线相等的菱形是正方形 C、对角线相等的四边形是矩形 D、对角线互相垂直且相等的四边形是正方形10. 下列图形中,能表示一次函数与正比例函数(m、n为常数)的图象的是( )A、 B、
B、 C、
C、 D、
D、 11. 如图,在平面直角坐标系中,菱形OABC的顶点A在y轴的正半轴上,点B在函数y=(x>0)的图象上,若点C的坐标为(4,3),则k的值为( )
11. 如图,在平面直角坐标系中,菱形OABC的顶点A在y轴的正半轴上,点B在函数y=(x>0)的图象上,若点C的坐标为(4,3),则k的值为( ) A、12 B、20 C、24 D、3212. 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:(1)、a=40,m=1;(2)乙的速度是80km/h;(3)甲比乙迟h到达B地;(4)乙车行驶小时或小时,两车恰好相距50km.
A、12 B、20 C、24 D、3212. 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:(1)、a=40,m=1;(2)乙的速度是80km/h;(3)甲比乙迟h到达B地;(4)乙车行驶小时或小时,两车恰好相距50km.正确的个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 在平面直角坐标系中,点 与点 关于 轴对称,则 的值是 .14. 在反比例函数的图象上有三个点,则的大小关系为 . (用“<”连接)15. 如图,四边形是矩形,的平分线交延长线于点E,若 , 则的长为 .
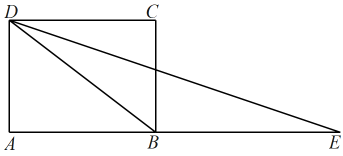 16. 如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,点G是EF的中点,连接CG,BG,BD,DG,下列结论:①BC=DF;②;③;④ , 则 , 正确的有 .
16. 如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,点G是EF的中点,连接CG,BG,BD,DG,下列结论:①BC=DF;②;③;④ , 则 , 正确的有 .
三、解答题
-
17.(1)、化简: .(2)、计算: .18. 如图,点D为的边BC的中点,过点A作 , 且 , 连接DE,CE.
 (1)、求证:;(2)、若 , 判断四边形ADCE的形状,并说明理由;(3)、若要使四边形ADCE为正方形,则应满足什么条件?
(1)、求证:;(2)、若 , 判断四边形ADCE的形状,并说明理由;(3)、若要使四边形ADCE为正方形,则应满足什么条件?(直接写出条件即可,不必证明).
19. 为了选拔一名学生参加全市诗词大赛,学校组织了四次测试,其中甲乙两位同学成绩较为优秀,他们在四次测试中的成绩(单位:分)如下表所示甲
90
85
95
90
乙
98
82
88
92
(1)、分别求出两位同学在四次测试中的平均分;(2)、分别求出两位同学测试成绩的方差,若这次参赛目的是为了成绩稳定发挥,你认为选谁参加比赛更合适,请说明理由.20. “节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:(1)、A型自行车去年每辆售价多少元;(2)、该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多.21. 如图,在矩形中, , , 点是边的中点,反比例函数的图像经过点 , 交于点 . (1)、求的值及直线的解析式;(2)、在轴上找一点 , 使的周长最小,求此时点的坐标;(3)、在(2)的条件下,求的面积.22. 如图①,的顶点P是正方形两条对角线的交点, , 将绕点P旋转,旋转过程中的两边分别与正方形的边和交于点E和点F(点F与点C,D不重合)
(1)、求的值及直线的解析式;(2)、在轴上找一点 , 使的周长最小,求此时点的坐标;(3)、在(2)的条件下,求的面积.22. 如图①,的顶点P是正方形两条对角线的交点, , 将绕点P旋转,旋转过程中的两边分别与正方形的边和交于点E和点F(点F与点C,D不重合) (1)、如图①,当时,之间满足的数量关系是;(2)、如图②,将图①中的正方形改为的菱形,M是中点,其他条件不变,当时,求证: .(3)、在(2)的条件下,若旋转过程中的边与线段延长线交于点E,其他条件不变,探究在整个运动变化过程中,之间满足的数量关系.
(1)、如图①,当时,之间满足的数量关系是;(2)、如图②,将图①中的正方形改为的菱形,M是中点,其他条件不变,当时,求证: .(3)、在(2)的条件下,若旋转过程中的边与线段延长线交于点E,其他条件不变,探究在整个运动变化过程中,之间满足的数量关系.