四川省雅安市2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-28 类型：期末考试

进入出卷网下载

一、单选题

1. $- 3$ 的绝对值是（）

A、 $\frac{1}{3}$ B、 $- \frac{1}{3}$ C、3 D、 $\sqrt{3}$

查看试题解析
2. 下列算式的运算结果为 $a^{6}$ 的是（）

A、 $a^{3} \cdot a^{2}$ B、 ${(a^{3})}^{2}$ C、 $a^{3} + a^{3}$ D、 $a^{12} \div a^{2}$

查看试题解析
3. 某几何体的三视图如图所示，该几何体是（）

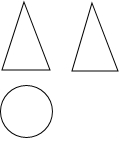A、圆锥 B、圆柱 C、三棱锥 D、球

查看试题解析
4. 如图， $A B ∥ C D$ ， $∠ A B E = 150 ° ， ∠ B E F = 70 °$ ，则 $∠ D F E$ 的度数为（）

A、 $30 °$ B、 $40 °$ C、 $50 °$ D、 $60 °$

查看试题解析
5. “一方有难，八方支援”是中华民族的优秀传统，在2008年5月汶川大地震后，全国各界纷纷捐款捐物．某企业捐款9840万元人民币，数9840万用科学记数法表示为（）

A、 $9.84 \times 1 0^{8}$ B、 $98.4 \times 1 0^{6}$ C、 $0.984 \times 1 0^{8}$ D、 $9.84 \times 1 0^{7}$

查看试题解析
6. 已知实数x、y满足 $\sqrt{x - 3} + {(y + 2)}^{2} = 0$ ，则 $2 x + y$ 的平方根是（）

A、 $\pm 2$ B、2 C、 $- 2$ D、 $\pm 4$

查看试题解析
7. 某公司为了了解一年内的用水量，抽查了其中10天的用水量，结果如表：
用水量（吨）
25
32
40
43
47
50
110
天数
1
1
1
2
3
1
1
关于这10天的用水量的统计分析，下列说法正确的是（）

A、众数是43 B、中位数是45 C、中位数是43 D、平均数是49.6

查看试题解析
8. a为正整数，且 $a < \sqrt{14} < a + 1$ ，则a的值为（）

A、2 B、3 C、4 D、5

查看试题解析
9. 已知点 $A (4 ， a - 5)$ 与点 $B (b - 1 ， - 3)$ 关于y轴对称，则 $a^{b}$ 的值为（）

A、 $- 6$ B、 $- 8$ C、 $\frac{1}{8}$ D、 $-$ $\frac{1}{8}$

查看试题解析
10. 小明从家骑共享单车去体育场锻炼一会儿后，又步行原路返回，途中在早餐店用餐，如图表示小明离家的距离y（千米）与离家的时间t（分）之间的函数关系，则下列说法错误的是（）

A、体育场离小明家4千米 B、小明从体育场到早餐店的平均速度 $4.8$ 千米/小时 C、小明吃早餐用了 $20$ 分钟 D、小明从早餐店回家的平均速度是3千米/小时

查看试题解析
11. 如图，在四边形 $A B C D$ 中，E、F分别是 $D C$ 、 $A D$ 的中点， $E F ⊥ A B$ ，若 $B C ＝ 13$ ， $A B ＝ 5$ ，则 $E F$ 的长度为（）

A、6 B、5 C、4 D、3

查看试题解析
12. 若关于x的分式方程 $\frac{2 m}{x - 1} + \frac{m}{x + 1} = \frac{4}{x^{2} - 1}$ 有增根，则m的值为（）

A、1 B、-2 C、1或 $- 2$ D、 $- 1$ 或2

查看试题解析

二、填空题

13. 若一个正多边形的每一个外角都是30°，则这个正多边形的内角和等于度.

查看试题解析
14. 一个不透明的袋子中装有6个红球，白球若干个，这些小球除颜色外无其他差别，从袋子中随机摸出一个小球是白球的概率是 $\frac{1}{4}$ ，则袋子中装有个白球．

查看试题解析
15. 如图，在平面直角坐标系中，点A的坐标为 $(0 ， 6)$ ，将 $△ A O B$ 沿x轴向左平移后得到 $△ A_{1} B_{1} C_{1}$ ，点 $A_{1}$ 在直线 $y = - x + 2$ 上，则点B与其对应点 $B_{1}$ 间的距离为．

查看试题解析

三、解答题

16. 先化简，再求值： $\frac{x}{x^{2} - 1} \div (\frac{1}{x + 1} - 1)$ ，其中 $x = \sqrt{2} + 1$ ．

查看试题解析
17. 某学校为教育学生珍惜粮食，准备提倡“光盘行动”，为了了解学生就餐时饭菜的剩余情况，随机抽取了部分学生进行调查，并将结果统计后绘制成了如图所示的不完整的统计图．

(1)、这次被调查的学生共有名，“剩大量”的百分比为，在扇形统计图中“剩一半左右”所对应的圆心角为度；

(2)、补全条形统计图；

(3)、估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐．据此估算，该校18000名学生一餐浪费的食物可供多少人食用一餐？

查看试题解析
18. 2022年北京冬奥会的吉祥物“冰墩墩”和“雪容融”深受国内外广大朋友的喜爱，某特许零售店准备购进一批吉祥物销售．已知购进3件“冰墩墩”和1件“雪容融”共用230元，购进2件“冰墩墩”和3件“雪容融”共用270元．

(1)、求“冰墩墩”和“雪容融”的进货单价各是多少元？

(2)、若该特许零售店购进“冰墩墩”和“雪容融”共100件，并且“雪容融”的数量不超过“冰墩墩”数量的3倍，该零售店如何安排进货方案，才能使进货费用最低，最低费用是多少元？

查看试题解析
19. 如图，在平面直角坐标系中，直线 $y = - 2 x + 4$ 分别交x轴、y轴于A、B两点，将 $△ A O B$ 绕点O逆时针旋转 $90 °$ 后得到 $△ A_{1} O B_{1}$ ．

(1)、求直线 $A_{1} B_{1}$ 的解析式；

(2)、若直线 $A_{1} B_{1}$ 与直线 $A B$ 交于点C，P是直线 $A B$ 上一点，当 $S_{△ P B_{1} A} = 5 S_{△ A B_{1} C}$ 时，求点P的坐标．

查看试题解析
20. 如图1，在 $Δ A B C$ 中， $∠ B A C ＝ 90 °$ ， $A B ＝ A C$ ，点D是边 $A C$ 上的动点，过点C作 $C E ⊥ B D$ 交 $B D$ 的延长线于点E．

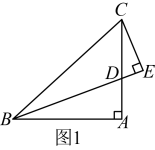(1)、如图2，延长 $C E$ 交 $B A$ 的延长线于点F．

①求证： $Δ A B D ≌ Δ A C F$ ；
②若 $B D ＝ 2 C E$ ，求 $∠ E C D$ 的度数；

(2)、如图3，过点A作 $A G ⊥ B E$ 于点G，连接 $A E$ ，试探究线段 $B E$ 、 $C E$ 、 $A G$ 之间的数量关系，并说明理由．

查看试题解析
21. 我们来规定下面两种数：
①平方和数：若一个三位或者三位以上的正整数分成左、中、右三个数后满足：中间数＝（左边数）²+（右边数）² ，我们就称该整数是平方和数，例如：整数 $251$ ，它的中间数是5，左边数是2，右边数是1，∵ $2^{2} + 1^{2} = 5$ ， ∴ $251$ 是平方和数；再例如： $3254$ ， ∵ $3^{2} + 4^{2} = 25$ ， ∴ $3254$ 是一个平方和数；当然152， $4253$ 这两个数也肯定是平方和数；
②双倍积数：若一个三位或者三位以上的正整数分成左、中、右三个数后满足：中间数＝2×左边数×右边数，我们称该整数是双倍积数；例如：整数 $142$ ，它的中间数是4，左边数是1，右边数是2，∵ $2 \times 1 \times 2 = 4$ ， ∴ $142$ 是一个双倍积数；再例如： $3305$ ， ∵ $2 \times 3 \times 5 = 30$ ， ∴ $3305$ 是一个双倍积数；当然， $241$ ， $5303$ 也是一个双倍积数；
注意：在下列问题中，我们统一用字母a表示一个正整数分出来的左边数，用字母b表示一个正整数分出来的右边数，请根据上述定义完成下面问题：

(1)、如果一个三位正整数为平方和数，且十位数字是4，则该三位整数是；如果一个三位正整数为双倍积数，十位数字是8，则该三位整数是；

(2)、若一个正整数既是平方和数，又是双倍积数，试探究a、b的数量关系，并说明理由；

(3)、若正整数 $a 1125 b$ 为一个平方和数， $a 900 b$ 为一个双倍积数，求 $a^{2} - b^{2} + 2 b - 1$ 的值．

查看试题解析

四、填空题

22. 已知关于x的不等式组 ${\begin{array}{l} x > m + 2 \\ 2 x + 1 \leq - 4 m - 1 \end{array}$ 无解，且关于x的分式方程 $\frac{x}{x - 2} + \frac{m x + 4}{2 - x} = - 1$ 的解是正整数，则整数m的值为．

查看试题解析
23. 如图，在 $R t △ A B C$ 中， $∠ A C B = 9 0^{∘}$ ， $∠ A = 3 0^{∘}$ ，将 $△ A B C$ 绕点C逆时针旋转得到 $△ A_{1} B_{1} C_{1}$ ，点M是 $B C$ 的中点，点N是 $A_{1} B_{1}$ 的中点，连接 $M N$ ，若 $A B = 12$ ，则线段 $M N$ 的最大值是．

查看试题解析

五、解答题

24. 如图1，在平行四边形 $A B C D$ 中， $∠ A B C$ 的平分线交 $A D$ 于点E， $∠ A D C$ 的平分线交 $B C$ 于点F．

(1)、试探究四边形 $B F D E$ 的形状，并说明理由；

(2)、如图2，连接 $E F$ ，若 $E F ⊥ B C ， D E = 6 ， E F = 4$ ，求 $A E$ 的长；

(3)、如图3，连接 $E F$ ，将 $△ E A B$ 沿直线 $E F$ 翻折得到 $△ E C G$ ，其中点A、B的对应点分别为点C、G，恰好有 $G E ⊥ D F$ ，垂足为点N， $E C$ 交 $D F$ 于点M．
①试探究 $△ D E C$ 的形状，并说明理由；

②若 $D F = 2 + \sqrt{2}$ ，求 $E F$ 的长．

查看试题解析

用水量（吨）	25	32	40	43	47	50	110
天数	1	1	1	2	3	1	1