四川省资阳市2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-28 类型:期末考试
一、单选题
-
1. 若分式有意义,则的取值范围是( )A、 B、 C、 D、2. 在中,若 , 则的度数为( )A、 B、 C、 D、3. 已知、两点关于轴对称,则的值为( )A、5 B、1 C、 D、4. 一衬衫专卖店店主,对上周部分尺码的衬衫销售情况统计如表:
尺码
40
41
42
43
44
平均每天销售数量
2
3
5
1
1
该店主决定本周进货时,增加一些42码的衬衫,影响该店主决策的统计量是( )
A、平均数 B、中位数 C、众数 D、方差5. 下列说法错误的是( )A、平行四边形的对边相等 B、菱形的每条对角线平分一组对角 C、正方形既是轴对称图形、又是中心对称图形 D、矩形的对角线互相垂直平分6. 若关于的方程有增根,则的值为( )A、 B、 C、 D、7. 如图,在正方形中,是对角线上一点,的延长线交于点 , 连接 . 若 , 则的度数为( )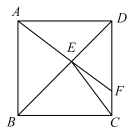 A、 B、 C、 D、8. 在同一坐标系中,函数y= 和y=kx﹣k的图象大致是( )A、
A、 B、 C、 D、8. 在同一坐标系中,函数y= 和y=kx﹣k的图象大致是( )A、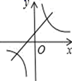 B、
B、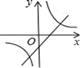 C、
C、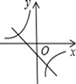 D、
D、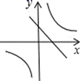 9.
9.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )
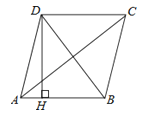 A、 B、 C、12 D、2410. 如图,在矩形中, , 点、分别在边、上,将沿折叠,使点落在边上的点处,将沿折叠,使点落在上的点处.若 , , 则的长为( )
A、 B、 C、12 D、2410. 如图,在矩形中, , 点、分别在边、上,将沿折叠,使点落在边上的点处,将沿折叠,使点落在上的点处.若 , , 则的长为( )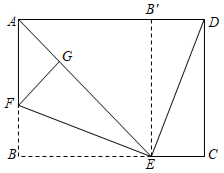 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
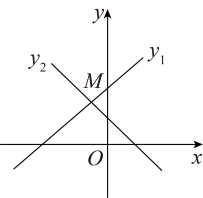
11. 计算: .12. 某植物一粒花粉的质量约为毫克,将数“”用科学记数法表示为 .13. 小强参加某公司新员工应聘的笔试成绩为80分,面试成绩为90分,若笔试成绩、面试成绩按计算平均成绩,则小强的平均成绩是分.14. 如图,直线与直线相交于点 , 则关于的不等式的解集为 .
 15. 如图,在中,、分别是、的平分线,若 , , 则的长为 .
15. 如图,在中,、分别是、的平分线,若 , , 则的长为 .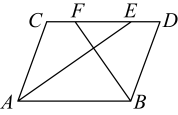 16. 已知直线的解析式为 , 菱形 , , , …按图所示的方式放置,顶点 , , , , …均在直线上,顶点 , , , …均在轴上,则点的坐标是 .
16. 已知直线的解析式为 , 菱形 , , , …按图所示的方式放置,顶点 , , , , …均在直线上,顶点 , , , …均在轴上,则点的坐标是 .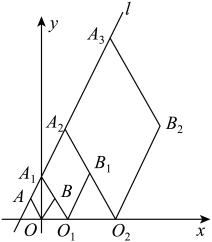
三、解答题
-
17. 先化简,再求值: , 其中 .18. 为加强爱国主义教育,某校决定开展四项党史教育活动(每人均限报一项):A.党史演讲比赛;B.党史手抄报比赛;C.党史知识竞赛;D.红色歌咏比赛,为了解学生的报名情况,对其进行随机抽样调查,将调查结果绘制成图所示的统计图.
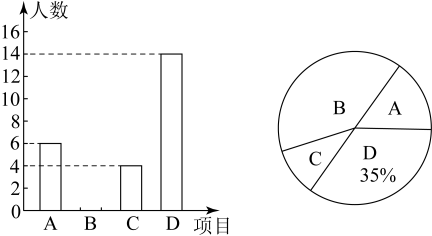
请结合图中信息,解答下列问题:
(1)、本次共调查了 ▲ 名学生,请将条形统计图补充完整;(2)、已知该校八年级有700名学生,请你估计该校八年级学生中报名参加“党史手抄报比赛”的人数.19. 如图,在菱形中,、相交于点 , 是的中点,连接 , 过点作交的延长线于点 , 连结 .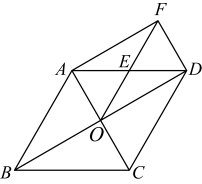 (1)、求证:;(2)、试判断四边形的形状,并说明理由.20. 王先生开轿车从地出发,前往地,路过服务区并休息一段时间后,继续以原速度行驶,到达地,又休息了一段时间,然后开轿车接原路返回地,速度是原来的倍.王先生距离地的路程与出发后所用的时间之间的函数图象如图所示.
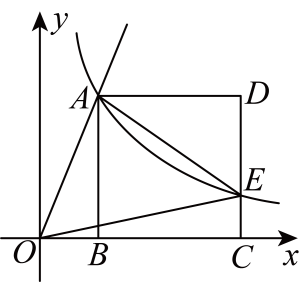
(1)、求证:;(2)、试判断四边形的形状,并说明理由.20. 王先生开轿车从地出发,前往地,路过服务区并休息一段时间后,继续以原速度行驶,到达地,又休息了一段时间,然后开轿车接原路返回地,速度是原来的倍.王先生距离地的路程与出发后所用的时间之间的函数图象如图所示.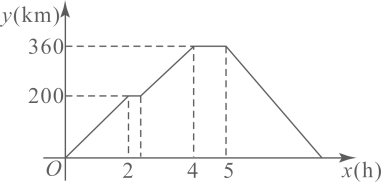 (1)、王先生从地到地的逾中,休息了;(2)、求王先生从地返回地所用的时间.(3)、当王先生从地返回地,再次到达服务区时,求的值.21. 如图,一次函数与反比例函数的图象交于、两点,与轴交于点.
(1)、王先生从地到地的逾中,休息了;(2)、求王先生从地返回地所用的时间.(3)、当王先生从地返回地,再次到达服务区时,求的值.21. 如图,一次函数与反比例函数的图象交于、两点,与轴交于点.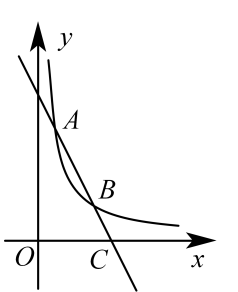 (1)、求一次函数与反比例函数的解析式;(2)、若点在轴上,且的面积为 , 求点的坐标.22. 一商场正在销售A、B两种型号的冰箱,已知销售A型冰箱所获利润为2000元时的数量与销售B型冰箱所获利润为2500元时的数量相同,且销售1台B型冰箱的利润比销售1台A型冰箱的利润多50元.(1)、分别求出A、B两种型号冰箱每台的销售利润;(2)、该商场计划购进这两种型号的冰箱共80台,其中B型水箱的进货量不超过A型冰箱的2倍,则该商店应如何安排进货,才能使销售总利润最大?
(1)、求一次函数与反比例函数的解析式;(2)、若点在轴上,且的面积为 , 求点的坐标.22. 一商场正在销售A、B两种型号的冰箱,已知销售A型冰箱所获利润为2000元时的数量与销售B型冰箱所获利润为2500元时的数量相同,且销售1台B型冰箱的利润比销售1台A型冰箱的利润多50元.(1)、分别求出A、B两种型号冰箱每台的销售利润;(2)、该商场计划购进这两种型号的冰箱共80台,其中B型水箱的进货量不超过A型冰箱的2倍,则该商店应如何安排进货,才能使销售总利润最大?