四川省自贡市2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-28 类型:期末考试
一、单选题
-
1. 下列各式中,最简二次根式是( )A、 B、 C、 D、2. 下列各式计算正确的是( )A、 B、 C、 D、3. 已知一次函数的图象如图所示,则 , 的取值范围是( )
 A、 , B、 , C、 , D、 ,4. 矩形具有而菱形不具有的性质是( )A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、对角线平分一组对角5. 如图,在平面直角坐标系中,直线与直线相交于点 , 则关于 , 的二元一次方程组的解是( )
A、 , B、 , C、 , D、 ,4. 矩形具有而菱形不具有的性质是( )A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、对角线平分一组对角5. 如图,在平面直角坐标系中,直线与直线相交于点 , 则关于 , 的二元一次方程组的解是( ) A、 B、 C、 D、6. 在学校举办的学习强国演讲比赛中,李华根据九位评委所给的分数制作了如下表格:
A、 B、 C、 D、6. 在学校举办的学习强国演讲比赛中,李华根据九位评委所给的分数制作了如下表格:平均数
中位数
众数
方差
8.5
8.3
8.1
0.15
如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
A、平均数 B、众数 C、方差 D、中位数7. 如图,是一张直角三角形的纸片,两直角边 ,现将 折叠,使点B点A重合,折痕为DE,则BD的长为( ) A、7 B、 C、6 D、8. 如图,在中, , , , 点是斜边上的一个动点,过点分别作于点于点 , 点为四边形对角线交点,则线段的最小值为( )
A、7 B、 C、6 D、8. 如图,在中, , , , 点是斜边上的一个动点,过点分别作于点于点 , 点为四边形对角线交点,则线段的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
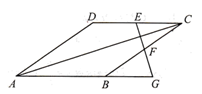
9. 如果式子有意义,则的取值范围为 .10. 点在一次函数的图象上,则等于 .11. 有一棵9米高的大树距离地面4米处折断.(未完全断开),则大树顶端触地点距大树的距离为米.12. 一组从小到大排列的数据:2,5,x,y,11,2x的平均数与中位数都是8,则 .13. 如图,在菱形ABCD中, , ,E,F分别是CD和BC的中点,连接EF并延长与AB的延长线相交于点G,则EG的长度为cm.
 14. 如图,矩形两边与坐标轴正半轴重合,是边上的一个动点,是经过 , 两点的直线上的一个动点,则的最小值是 .
14. 如图,矩形两边与坐标轴正半轴重合,是边上的一个动点,是经过 , 两点的直线上的一个动点,则的最小值是 .
三、解答题
-
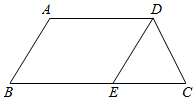
15. 计算: .16. 已知 , , 求的值.17. 如图,在四边形ABCD中,AD∥BC,∠B=∠C.E是边BC上一点,且DE=DC.求证:AD=BE.
 18. 如图,在中,的垂直平分线交于点 , 交于点 . 已知 , , . 求的面积.
18. 如图,在中,的垂直平分线交于点 , 交于点 . 已知 , , . 求的面积. 19. 已知一次函数的图象经过点和 .(1)、求出该函数的解析式;(2)、求出该函数图象与轴的交点坐标.20. 某校为了解学生的身高情况,对本校学生进行了抽样调查.已知抽取的样本中男生和女生的人数相同,利用所得数据绘制成如下所示的统计图表:
19. 已知一次函数的图象经过点和 .(1)、求出该函数的解析式;(2)、求出该函数图象与轴的交点坐标.20. 某校为了解学生的身高情况,对本校学生进行了抽样调查.已知抽取的样本中男生和女生的人数相同,利用所得数据绘制成如下所示的统计图表:身高情况分组表(单位:cm)
组别
身高
A
B
C
D
E
男生身高情况频数分布直方图 女生身高情况扇形统计图

根据图表提供的信息,回答下列问题:
(1)、在样本中,男生身高的众数在组,中位数在组;(2)、在样本中,女生身高在E组的人数为;(3)、已知该校共有男生400人、女生500人,请估计该校身高在之间的学生共有多少人.21. 已知的两条直角边及斜边长分别为 , 斜边上的高是 .求证: .
22. 如图1,在矩形纸片中, , , 折叠纸片使点落在上的点处,折痕为 , 过点作EF//AB交于点.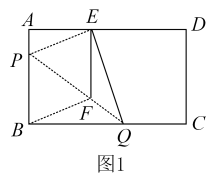
 (1)、求证:四边形为菱形;(2)、当折痕的点与点重合时(如图2),求菱形的边长.23. 在平面直角坐标系中,已知点 , , 根据勾股定理,我们可以求得这两个这点间的距离 . 当点在坐标轴上或平行(垂直)于坐标轴的直线上时,两点间的距离可简化为 , 或 .
(1)、求证:四边形为菱形;(2)、当折痕的点与点重合时(如图2),求菱形的边长.23. 在平面直角坐标系中,已知点 , , 根据勾股定理,我们可以求得这两个这点间的距离 . 当点在坐标轴上或平行(垂直)于坐标轴的直线上时,两点间的距离可简化为 , 或 .请利用以上结论,回答下列问题:
(1)、已知 , , 则两点间的距离为;(2)、已知在平行于轴的直线上,点的横坐标为5,点的横坐标为-2,则点两之间的距离为;(3)、已知一个三角形各顶点的坐标为 , , , 请判定此三角形的形状,并说明理由.24. 如图,在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 过点的另一条直线交轴正半轴于点 , 且 . (1)、求直线的解析式;(2)、如图1,过点的直线交线段于点的面积是面积的两倍,求点的坐标;(3)、如图2,点是线段的中点,点为轴上一动点,连接 , 以为边向右侧作正方形 , 在点的运动过程中,当顶点落在直线上时,求点的坐标.
(1)、求直线的解析式;(2)、如图1,过点的直线交线段于点的面积是面积的两倍,求点的坐标;(3)、如图2,点是线段的中点,点为轴上一动点,连接 , 以为边向右侧作正方形 , 在点的运动过程中,当顶点落在直线上时,求点的坐标.