广东省深圳市重点中学2023-2024学年高三上册数学8月开学摸底试卷
试卷更新日期:2023-08-28 类型:月考试卷
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 已知 , 则( )A、 B、 C、 D、2. 已知复数满足 , 则的共轭复数( )A、 B、 C、 D、3. 已知曲线在点处的切线方程为 , 则( )A、 B、 C、 D、4. 函数在区间上的图象大致为( )A、
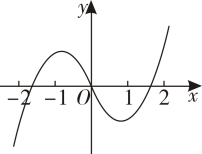 B、
B、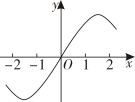 C、
C、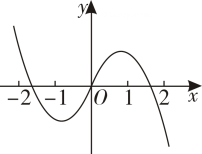 D、
D、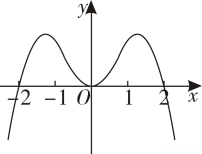 5. 为丰富同学们的暑假生活,暑假期间学校给同学们安排了6场线上讲座,其中讲座只能安排在第一或最后一场,讲座和必须相邻,问不同的安排方法共有( )A、144种 B、96种 C、56种 D、34种6. 现随机安排甲、乙等4位同学参加校运会跳高、跳远、投铅球比赛,要求每位同学参加一项比赛,每项比赛至少一位同学参加,事件“甲参加跳高比赛”,事件“乙参加跳高比赛”,事件“乙参加跳远比赛”,则( )A、事件与相互独立 B、事件与为互斥事件 C、 D、7. 分别是双曲线的左、右焦点,直线为双曲线的一条渐近线,关于直线的对称点为 , 且在以为圆心、为半径的圆上,则双曲线的离心率为( )A、 B、 C、2 D、8. 符号表示不超过实数的最大整数,如.已知数列满足 , .若为数列的前项和,则( )A、2023 B、2024 C、2025 D、2026
5. 为丰富同学们的暑假生活,暑假期间学校给同学们安排了6场线上讲座,其中讲座只能安排在第一或最后一场,讲座和必须相邻,问不同的安排方法共有( )A、144种 B、96种 C、56种 D、34种6. 现随机安排甲、乙等4位同学参加校运会跳高、跳远、投铅球比赛,要求每位同学参加一项比赛,每项比赛至少一位同学参加,事件“甲参加跳高比赛”,事件“乙参加跳高比赛”,事件“乙参加跳远比赛”,则( )A、事件与相互独立 B、事件与为互斥事件 C、 D、7. 分别是双曲线的左、右焦点,直线为双曲线的一条渐近线,关于直线的对称点为 , 且在以为圆心、为半径的圆上,则双曲线的离心率为( )A、 B、 C、2 D、8. 符号表示不超过实数的最大整数,如.已知数列满足 , .若为数列的前项和,则( )A、2023 B、2024 C、2025 D、2026二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
-
9. 已知 , 则下列结论正确的是( )A、 B、 C、 D、10. 若 , 则下列命题正确的是( )A、若且 , 则 B、若 , 则 C、若且 , 则 D、11. 如图,在正方体中,均是所在棱的中点,则下列说法正确的是( )
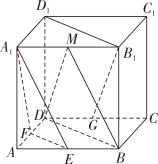 A、 B、平面 C、平面平面 D、12. 已知函数及其导函数满足 , 且 , 则( )A、在上单调递增 B、在上有极小值 C、的最小值为 D、的最小值为0
A、 B、平面 C、平面平面 D、12. 已知函数及其导函数满足 , 且 , 则( )A、在上单调递增 B、在上有极小值 C、的最小值为 D、的最小值为0三、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卡相应横线上.
-
13. 的展开式中,项的系数为.14. 如果平面向量 , 那么向量在上的投影向量为.15. 已知正数满足 , 则函数的定义域为.16. 如图,直三棱柱中, , , 点在棱上,且 , 当的面积取最小值时,三棱锥的外接球的表面积为.
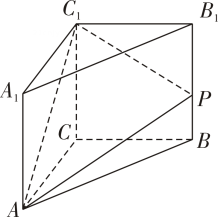
四、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.
-
17. 在中,内角所对的边分别为 , 已知 , 且.(1)、求的值;(2)、求的面积;18. 已知数列各项都不为0,前项和为 , 且 , 数列满足.(1)、求数列和的通项公式;(2)、令 , 求数列的前项和为.19. 某研究机构为了解某地年轻人的阅读情况,通过随机抽样调查了100位年轻人,对这些人每天的阅读时间(单位:分钟)进行统计,得到样本的频率分布直方图,如图所示.
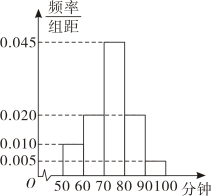 (1)、根据频率分布直方图,估计这100位年轻人每天阅读时间的平均数(单位:分钟);(同一组数据用该组数据区间的中点值表示)(2)、若年轻人每天阅读时间近似地服从正态分布 , 其中近似为样本平均数 , 求;(3)、为了进一步了解年轻人的阅读方式,研究机构采用分层抽样的方法从每天阅读时间位于分组的年轻人中抽取10人,再从中任选3人进行调查,求抽到每天阅读时间位于的人数的分布列和数学期望.
(1)、根据频率分布直方图,估计这100位年轻人每天阅读时间的平均数(单位:分钟);(同一组数据用该组数据区间的中点值表示)(2)、若年轻人每天阅读时间近似地服从正态分布 , 其中近似为样本平均数 , 求;(3)、为了进一步了解年轻人的阅读方式,研究机构采用分层抽样的方法从每天阅读时间位于分组的年轻人中抽取10人,再从中任选3人进行调查,求抽到每天阅读时间位于的人数的分布列和数学期望.参考数据:若 , 则①;②;③.
