2023-2024学年初中数学七年级上册 2.1 用字母表示数 同步分层训练培优卷(湘教版)
试卷更新日期:2023-08-25 类型:同步测试
一、选择题
-
1. 若A种糖的单价为元/千克,B种糖的单价为元/千克,则m千克A种糖和n千克B种糖混合而成的什锦糖的单价为( )A、元/千克 B、元/千克 C、元/千克 D、元/千克2. 某种商品进价为a元,在销售旺季,提价30%销售,旺季过后,商品以7折价格开展促销活动,这时一件商品的售价为( )A、a B、0.7a C、1.03a D、0.91a3. 如图是同一时刻北京时间和莫斯科时间.若现在北京时间是x,则同一时刻莫斯科的时间可以表示为( )
 A、 B、 C、 D、4. 如图,四边形是一个长方形,利用不同的方法可以计算出长方形的面积.通过分析图形中所标线段的长度,将多项式因式分解,其结果正确的是( )
A、 B、 C、 D、4. 如图,四边形是一个长方形,利用不同的方法可以计算出长方形的面积.通过分析图形中所标线段的长度,将多项式因式分解,其结果正确的是( )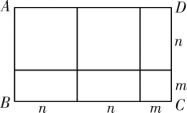 A、 B、 C、 D、5. 把长和宽分别为a和b的四个相同的小长方形按不同的方式拼成如图1的正方形和如图2的大长方形这两个图形,由两图形中阴影部分面积之间的关系正好可以验证下面等式的正确性的是( )
A、 B、 C、 D、5. 把长和宽分别为a和b的四个相同的小长方形按不同的方式拼成如图1的正方形和如图2的大长方形这两个图形,由两图形中阴影部分面积之间的关系正好可以验证下面等式的正确性的是( )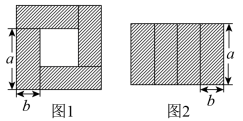 A、 B、 C、 D、6. 苹果原价是每斤元,现在按8折出售,假如现在要买一斤,那么需要付费A、元 B、元 C、元 D、元7. 如图,正方形与正方形 , 点在边上,已知正方形的边长 , 正方形的边长为 , 用、表示下列面积,与相交于点 , 下列各选项中错误的是( )
A、 B、 C、 D、6. 苹果原价是每斤元,现在按8折出售,假如现在要买一斤,那么需要付费A、元 B、元 C、元 D、元7. 如图,正方形与正方形 , 点在边上,已知正方形的边长 , 正方形的边长为 , 用、表示下列面积,与相交于点 , 下列各选项中错误的是( ) A、 B、 C、 D、8. 如图,大矩形分割成五个小矩形,④号、⑤号均为正方形,其中⑤号正方形边长为1.若②号矩形的长与宽的差为2,则知道哪个小矩形的周长,就一定能算出这个大矩形的面积( )
A、 B、 C、 D、8. 如图,大矩形分割成五个小矩形,④号、⑤号均为正方形,其中⑤号正方形边长为1.若②号矩形的长与宽的差为2,则知道哪个小矩形的周长,就一定能算出这个大矩形的面积( )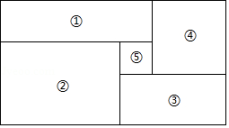 A、①或③ B、② C、④ D、以上选项都可以
A、①或③ B、② C、④ D、以上选项都可以二、填空题
-
9. 某商品原价为a元,经营者连续两次提价,两次分别提价10%.后因市场物价调整,又一次性降价20%,则这种商品的现价是元.10. 三张大小相同的正方形纸片粘贴成如图所示的形状放在地上,相邻两张纸片的重叠部分为小正方形.若一个小正方形的面积为S,且每个大正方形的面积比每个小正方形的面积的2倍还大4,则被这三张纸片遮盖的地面面积为(用含S的代数式表示).
 11. 如图所示,一块砖的外墙面积为x,那么图中残缺墙面的面积为.
11. 如图所示,一块砖的外墙面积为x,那么图中残缺墙面的面积为. 12. 三个长方形纸片如图1所示无缝隙地拼接在一起,它们的边长分别标记在图1中.现将拼接后的纸片用图2所示方式重新分割成三个长方形A,B,C.根据图2与图1的关系写出一个等式:(用含a,b,c,d,e,f的式子表示).
12. 三个长方形纸片如图1所示无缝隙地拼接在一起,它们的边长分别标记在图1中.现将拼接后的纸片用图2所示方式重新分割成三个长方形A,B,C.根据图2与图1的关系写出一个等式:(用含a,b,c,d,e,f的式子表示). 13. 有一个长方体水箱,从里面量得它的深度为 , 底面长为 , 宽为 , 水箱里已盛有深度为的水.若往水箱里放入一个棱长为的立方体铁块,则水箱的水深为.
13. 有一个长方体水箱,从里面量得它的深度为 , 底面长为 , 宽为 , 水箱里已盛有深度为的水.若往水箱里放入一个棱长为的立方体铁块,则水箱的水深为.三、解答题
-
14. 如图,用字母表示图中阴影部分的面积.
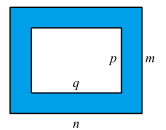 15. 如图是某居民小区的一块长为b米,宽为2a米的长方形空地,为了美化环境,准备在这个长方形的四个顶点处各修建一个半径为a米的扇形花台,然后在花台内种花,其余部分种草.如果建造花台及种花费用每平方米需要资金100元,种草每平方米需要资金50元,那么美化这块空地共需资金多少元?
15. 如图是某居民小区的一块长为b米,宽为2a米的长方形空地,为了美化环境,准备在这个长方形的四个顶点处各修建一个半径为a米的扇形花台,然后在花台内种花,其余部分种草.如果建造花台及种花费用每平方米需要资金100元,种草每平方米需要资金50元,那么美化这块空地共需资金多少元?
四、综合题
-
16. 如图
 (1)、【操作感知】如图①,长方形透明纸上有一条数轴,是周长为4的圆的直径,点与数轴原点重合,将圆从原点出发沿数轴正方向滚动1周,点落在数轴上的点处;将圆从原点出发沿数轴负方向滚动半周,点落在数轴上的点处,折叠长方形透明纸,使数轴上的点与点重合,此时折痕与数轴交点表示的数为.(2)、【建立模型】折叠长方形透明纸,使得数轴上表示数的点与表示数的点重合,则折痕与数轴交点表示的数为(用含 , 的代数式表示).(3)、【问题解决】若 , , 为数轴上不同的三点,点表示的数为 , 点表示的数为-2,如果 , , 三点中的一点到其余两点的距离相等,求点表示的数;(4)、如图②,若是周长为的圆的直径,点与数轴原点重合,将圆从原点出发沿数轴正方向滚动2周,点落在数轴上的点处;将圆从原点出发沿数轴负方向滚动周,点落在数轴上的点处.将此长方形透明纸沿 , 剪开,将点 , 之间一段透明纸对折,使其左、右两端重合,这样连续对折次后,再将其展开,求最右端折痕与数轴交点表示的数.17. 阅读以下材料,并解答问题.
(1)、【操作感知】如图①,长方形透明纸上有一条数轴,是周长为4的圆的直径,点与数轴原点重合,将圆从原点出发沿数轴正方向滚动1周,点落在数轴上的点处;将圆从原点出发沿数轴负方向滚动半周,点落在数轴上的点处,折叠长方形透明纸,使数轴上的点与点重合,此时折痕与数轴交点表示的数为.(2)、【建立模型】折叠长方形透明纸,使得数轴上表示数的点与表示数的点重合,则折痕与数轴交点表示的数为(用含 , 的代数式表示).(3)、【问题解决】若 , , 为数轴上不同的三点,点表示的数为 , 点表示的数为-2,如果 , , 三点中的一点到其余两点的距离相等,求点表示的数;(4)、如图②,若是周长为的圆的直径,点与数轴原点重合,将圆从原点出发沿数轴正方向滚动2周,点落在数轴上的点处;将圆从原点出发沿数轴负方向滚动周,点落在数轴上的点处.将此长方形透明纸沿 , 剪开,将点 , 之间一段透明纸对折,使其左、右两端重合,这样连续对折次后,再将其展开,求最右端折痕与数轴交点表示的数.17. 阅读以下材料,并解答问题.

阅读一:画与三角形面积相等的长方形.
(1)、如图1,已知 , ①画边上的高;②取线段的中点E;③以为边画长方形 , 使得那么长方形的面积等于的面积.根据“阅读一”,如果 , 那么长方形的面积= ▲ .
阅读二:画与长方形面积相等的正方形.
如图2,已知长方形 , ①延长 , 截取;
②以的中点O为圆心,为半径作半圆;
③过点F画 的垂线,交半圆于点I;④以为边画正方形那么正方形的面积等于长方形的面积.
(2)、根据“阅读二”,设 , 如果等面积的正方形边长为5,请猜想a、b的数量关系并加以说明;(3)、根据“阅读一”由画出它的等面积长方形 , 在长方形的基础上,再根据“阅读二”画出等面积正方形FIJK,设 , 当H为的中点时,m、n的数量关系为: .