上海市闵行区2022-2023学年高一下学期期末数学试题

试卷更新日期：2023-08-24 类型：期末考试

进入出卷网下载

一、填空题

1. 函数 $y = t a n x$ 的最小正周期是．

查看试题解析
2. 若复数 $z = i - 1$ ，则 $| z + 1 | =$ .

查看试题解析
3. 已知角α的终边经过点(3，4)，则cosα=.

查看试题解析
4. 已知 $s i n x = - \frac{1}{2}$ ， $x \in [- \frac{π}{2} ， \frac{π}{2}]$ ，则角 $x =$ .

查看试题解析
5. 若函数 $y = 3 c o s x - A s i n x (A > 0)$ 的最大值为 $\sqrt{13}$ ，则 $A =$ .

查看试题解析
6. 已知 $c o t θ = 2$ ，则 $\frac{c o s θ}{s i n θ + c o s θ}$ 的值为.

查看试题解析
7. 已知向量 $\vec{a}$ ， $\vec{b}$ 的夹角为 $\frac{π}{3}$ ， $\vec{a} = (2 ， 0)$ ，则 $\vec{a}$ 在 $\vec{b}$ 方向上的数量投影为.

查看试题解析
8. 若 $1 + 2 i$ 是关于 $x$ 的实系数一元二次方程 $x^{2} - 2 x + m = 0$ 的一个根，则 $m =$ ．

查看试题解析
9. 已知 $\vec{a} = (2 ， - 3)$ ， $\vec{b} = (0 ， k)$ ， $\vec{a}$ 与 $2 \vec{a} + \vec{b}$ 平行，则实数 $k$ 的值为.

查看试题解析
10. 在平面直角坐标系中，角 $α$ 的终边与角 $β$ 的终边关于 $y$ 轴对称．若 $t a n α = \frac{1}{2}$ ，则 $t a n 2 β =$ .

查看试题解析
11. 已知函数 $y = f (x)$ 的定义域为 $[0 ， + \infty)$ ，且当 $x \in [(n - 1) π ， n π]$ 时， $f (x) = \frac{1}{n} s i n (n x)$ ，其中 $n$ 取一切正整数.函数 $y = f (x)$ 的图像与直线 $y = m (m > 0)$ 恰有24个交点，则实数 $m$ 的取值范围是.

查看试题解析
12. 已知平面向量 $\vec{a_{1}}$ 、 $\vec{a_{2}}$ 、 $\vec{a_{3}}$ 、 $\vec{b_{1}}$ 、 $\vec{b_{2}}$ 、 $\vec{b_{3}}$ 两两互不相等，且 $| \vec{a_{1}} - \vec{a_{2}} | = | \vec{a_{2}} - \vec{a_{3}} | = | \vec{a_{3}} - \vec{a_{1}} | = 2$ .若对任意的 $i ， j \in {1 ， 2 ， 3}$ ，均满足 $| {\vec{a}}_{i} - {\vec{b}}_{j} | \in {1 ， \sqrt{3}}$ ，则当 $p ， q \in {1 ， 2 ， 3}$ 且 $p \neq q$ 时， $| \vec{b_{p}} - \vec{b_{q}} |$ 的值为.

查看试题解析

二、单选题

13. 复数 $z = i \cdot (1 - i)$ 的虚部为（）

A、 $1$ B、 $- 1$ C、 $i$ D、 $- i$

查看试题解析
14. 下列命题中正确的是（）

A、 $\vec{a} + (- \vec{a}) = 0$ B、 $\vec{0} \cdot \vec{a} = 0$ C、若 $| \vec{a} | = | \vec{b} |$ ，则 $\vec{a} = \vec{b}$ D、若 ${\vec{a}}^{2} = {\vec{b}}^{2}$ ，则 $\vec{a} = \vec{b}$

查看试题解析
15. 某同学将两角和的正弦、余弦、余切公式错误地记成如下三个式子：
① $s i n (α + β) = s i n α c o s α + s i n β c o s β$ ② $c o s (α + β) = c o s α c o s β + s i n α s i n β$ ；③ $c o t (α + β) = \frac{c o t α + c o t β}{1 - c o t α c o t β}$ ；

若存在 $α$ 、 $β$ 恰巧能使上述某些式子成立，则能成立的式子最多有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
16. 在复平面上，设点 $A$ 、 $B$ 对应的复数分别为 $- 2 i$ 、 $c o s (t - \frac{π}{3}) + i s i n (t - \frac{π}{3})$ ，当 $t$ 由 $\frac{π}{6}$ 连续变到 $\frac{π}{2}$ 时，向量 $\vec{A B}$ 所扫过的图形区域的面积是（）

A、 $\frac{\sqrt{3}}{4}$ B、 $\frac{π}{6}$ C、 $\frac{π}{4}$ D、 $\frac{\sqrt{3}}{4} + \frac{π}{12}$

查看试题解析

三、解答题

17. 在矩形 $A B C D$ 中， $A B = 2$ ， $A D = 1$ ，点 $M$ 、 $N$ 分别是边 $B C$ 、 $C D$ 的中点，设向量 $\vec{A B} = \vec{a}$ ， $\vec{A D} = \vec{b}$

(1)、试用 $\vec{a} 、 \vec{b}$ 表示向量 $\vec{A M}$ 与 $\vec{A N}$ ；

(2)、求 $\vec{A M} \cdot \vec{A N}$ 的值.

查看试题解析
18. 欧拉公式 $e^{θ i} = c o s θ + i s i n θ$ 将自然对数的底数 $e$ ，虚数单位 $i$ ，三角函数 $s i n θ ， c o s θ$ 联系在一起，充分体现了数学的和谐美，被誉为“数学的天桥”，已知复数 $z_{0} ， z$ 满足 $z_{0} = 1 + i$ ， $\bar{z_{0}} \cdot z = e^{π i} + a i (a \in R)$ .

(1)、求 $| z_{0} |$ ， $\bar{z_{0}}$ ；

(2)、若复数 $z$ 是纯虚数，求 $a$ 的值.

查看试题解析
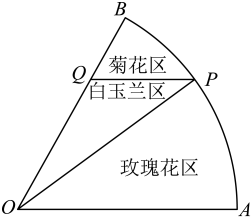19. 上海花博会的成功举办离不开对展览区域的精心规划.如图所示，将展区中扇形空地 $A O B$ 分隔成三部分建成花卉观赏区，分别种植玫瑰花、白玉兰和菊花.知扇形的半径为 $60$ 米， $∠ A O B = \frac{π}{3}$ ，动点 $P$ 在扇形 $A O B$ 的弧上，点 $Q$ 在半径 $O B$ 上，且 $P Q / / O A$ .

(1)、当 $O Q = 40$ 米时，求分隔栏 $P Q$ 的长；

(2)、综合考虑到成本和美观等原因，希望使白玉兰种植区的面积尽可能的大，求该种植区三角 $O P Q$ 的面积 $S$ 的最大值.

查看试题解析
20. 已知函数 $f (x) = A s i n (ω x + φ)$ ，其中 $ω > 0$ ， $| ϕ | < \frac{π}{2}$ ，分别求满足下列条件的函数 $y = f (x)$ 的解析式.

(1)、 $A = 2$ ， $ω = 1$ ， $f (\frac{π}{3}) = 2$ .

(2)、 $A = 2$ ， $x_{1}$ 、 $x_{2}$ 是 $y = f (x)$ 的两个相异零点， $| x_{1} - x_{2} |$ 的最小值为 $\frac{π}{2}$ ，且 $y = f (x)$ 的图像向右平移 $\frac{π}{12}$ 个单位长度后关于 $y$ 轴对称.

(3)、 $ω = \frac{π}{4}$ ， $f (4) = 3$ ，对任意的实数 $a$ ，记 $y = f (x)$ 在区间 $[a ， a + 2]$ 上的最大值为 $M (a)$ ，最小值为 $m (a)$ ， $h (a) = M (a) - m (a)$ ，函数 $y = h (a)$ 的值域为 $[6 - 3 \sqrt{2} ， 6 \sqrt{2}]$ .

查看试题解析
21. 通过平面直角坐标系，我们可以用有序实数对表示向量.类似的，我们可以把有序复数对 $(z_{1} ， z_{2}) (z_{1} ， z_{2} \in C)$ 看作一个向量，记 $\vec{a} = (z_{1} ， z_{2})$ ，则称 $\vec{a}$ 为复向量.类比平面向量的相关运算法则，对于 $\vec{a} = (z_{1} ， z_{2})$ ， $\vec{b} = (z_{3} ， z_{4})$ ， $z_{1}$ 、 $z_{2}$ 、 $z_{3}$ 、 $z_{4}$ 、 $λ \in C$ ，我们有如下运算法则：
① $\vec{a} \pm \vec{b} = (z_{1} \pm z_{3} ， z_{2} \pm z_{4})$ ；② $λ \vec{a} = (λ z_{1} ， λ z_{2})$ ；

③ $\vec{a} \cdot \vec{b} = z_{1} \bar{z_{3}} + z_{2} \bar{z_{4}}$ ；④ $| \vec{a} | = \sqrt{\vec{a} \cdot \vec{a}}$ .

(1)、设 $\vec{a} = (i ， 1 + i)$ ， $\vec{b} = (2 ， 2 - i)$ ，求 $\vec{a} + \vec{b}$ 和 $\vec{a} \cdot \vec{b}$ .

(2)、由平面向量的数量积满足的运算律，我们类比得到复向量的相关结论：
① $\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}$
② $\vec{a} \cdot (\vec{b} + \vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c}$
③ $(λ \vec{a}) \cdot \vec{b} = \vec{a} \cdot (λ \vec{b})$ .
试判断这三个结论是否正确，并对正确的结论予以证明.

(3)、若 $\vec{a} = (2 i ， 1)$ ，集合 $Ω = {\vec{p} | \vec{p} = (x ， y) ， y = 2 x + 1 ， x ， y \in C}$ ， $\vec{b} \in Ω$ .对于任意的 $\vec{c} \in Ω$ ，求出满足条件 $(\vec{a} - \vec{b}) \cdot (\vec{b} - \vec{c}) = 0$ 的 $\vec{b}$ ，并将此时的 $\vec{b}$ 记为 $\vec{b_{0}}$ ，证明对任意的 $\vec{b} \in Ω$ ，不等式 $| \vec{a} - \vec{b} | \geq | \vec{a} - \vec{b_{0}} |$ 恒成立.
根据对上述问题的解答过程，试写出一个一般性的命题（不需要证明）.

查看试题解析