云南省楚雄州2022-2023学年高一下学期期末考试数学试题
试卷更新日期:2023-08-24 类型:期末考试
一、单选题
-
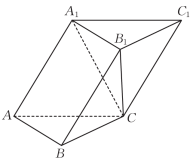
1. 已知集合 , 则( )A、 B、 C、 D、2. 复数的虚部为( )A、5 B、3 C、 D、3. 已知单位向量的夹角为 , 且 , 则( )A、 B、6 C、2 D、44. 已知样本数据的平均数为9,则另一组数据的平均数为( )A、 B、 C、4 D、35. 若是方程的解,则( )A、 B、 C、 D、6. 如图,在正方体中,分别是的中点,则异面直线与所成角的余弦值为( )
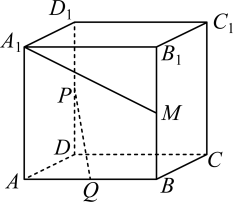 A、 B、 C、 D、7. “”是“对任意恒成立”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件8. “近水亭台草木欣,朱楼百尺回波濆”,位于济南大明湖畔的超然楼始建于元代,历代因战火及灾涝等原因,屡毁屡建.今天我们所看到的超然楼是2008年重建而成的,共有七层,站在楼上观光,可俯视整个大明湖的风景.如图,为测量超然楼的高度,选择C和一个楼房DE的楼顶为观测点,已知在水平地面上,超然楼和楼房都垂直于地面.已知 , 在点处测得点的仰角为 , 在点处测得点的仰角为 , 则超然楼的高度( )
A、 B、 C、 D、7. “”是“对任意恒成立”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件8. “近水亭台草木欣,朱楼百尺回波濆”,位于济南大明湖畔的超然楼始建于元代,历代因战火及灾涝等原因,屡毁屡建.今天我们所看到的超然楼是2008年重建而成的,共有七层,站在楼上观光,可俯视整个大明湖的风景.如图,为测量超然楼的高度,选择C和一个楼房DE的楼顶为观测点,已知在水平地面上,超然楼和楼房都垂直于地面.已知 , 在点处测得点的仰角为 , 在点处测得点的仰角为 , 则超然楼的高度( )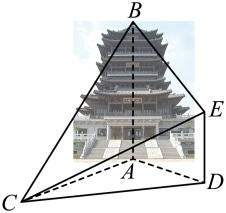 A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
9. 已知复数满足 , 则( )A、 B、是纯虚数 C、 D、复数在复平面内对应的点在第四象限10. 某饮料厂商开发了一种新的饮料,为了促销,每箱装的6瓶饮料中有2瓶瓶盖上分别印有“一等奖”,“二等奖”,其余4瓶印有“谢谢惠顾”.甲从新开的一箱中任选2瓶购买,设事件A表示“甲没有中奖”,事件B表示“甲获得一等奖”,事件C表示“甲中奖”,则( )A、事件A和事件B是对立事件 B、事件A和事件C是对立事件 C、 D、11. 下列式子计算正确的是( )A、 B、 C、 D、12. 在正三棱锥中,与底面所成角的余弦值为 , 则( )A、 B、三棱锥的体积为 C、二面角的大小为 D、三棱锥的外接球的表面积为
三、填空题
-
13. 某游客计划从海口市、三亚市、普洱市、昆明市、丽江市这5个地区中随机选择2个地区去旅行,其中海口市、三亚市属于海南省,普洱市、昆明市、丽江市属于云南省,则这2个地区在同一省的概率为.14. 若一个样本的中位数是4,则这个样本的方差为 , 这个样本的分位数为.15. 已知函数在上的最小值为 , 则的值为 .16. 已知外接圆的圆心为是边上一动点,若 , 则的最大值为.
四、解答题
-
17. 为了解学生对党的“二十大”精神的学习情况,学校开展了“二十大”相关知识的竞赛活动,全校共有1000名学生参加,其中男生550名,采用分层抽样的方法抽取100人,将他们的比赛成绩(成绩都在内)分为组,得到如图所示的频率分布直方图.
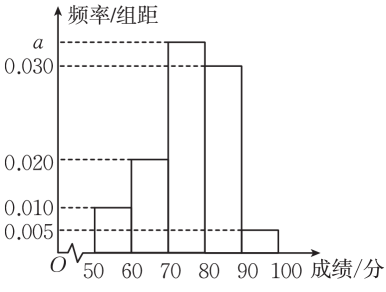 (1)、求的值以及女生被抽取的人数;(2)、估计这100人比赛成绩的分位数(小数点后保留2位).18. 已知函数且在区间上的最大值是2.(1)、求的值;(2)、若函数的定义域为 , 求不等式中的取值范围.19. 已知向量 , 设函数.(1)、求在上的单调增区间;(2)、若对任意恒成立,求的取值范围.20. 袋中装有大小完全相同的6个红球,3个蓝球,其中有2个红球和1个蓝球上面标记了数字1,其他球标记了数字2.(1)、每次有放回地任取1个小球,连续取两次,求取出的2个球恰有1个红球且两球的数字和为3的概率;(2)、从袋中不放回地依次取2个小球,每次取1个,记事件第一次取到的是红球 , 事件第二次取到了标记数字1的球 , 求 , 并判断事件与事件是否相互独立.
(1)、求的值以及女生被抽取的人数;(2)、估计这100人比赛成绩的分位数(小数点后保留2位).18. 已知函数且在区间上的最大值是2.(1)、求的值;(2)、若函数的定义域为 , 求不等式中的取值范围.19. 已知向量 , 设函数.(1)、求在上的单调增区间;(2)、若对任意恒成立,求的取值范围.20. 袋中装有大小完全相同的6个红球,3个蓝球,其中有2个红球和1个蓝球上面标记了数字1,其他球标记了数字2.(1)、每次有放回地任取1个小球,连续取两次,求取出的2个球恰有1个红球且两球的数字和为3的概率;(2)、从袋中不放回地依次取2个小球,每次取1个,记事件第一次取到的是红球 , 事件第二次取到了标记数字1的球 , 求 , 并判断事件与事件是否相互独立.