上海市虹口区2022-2023学年高二下学期期末数学试题
试卷更新日期:2023-08-24 类型:期末考试
一、填空题
-
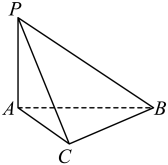
1. 若直线:.与直线:互相垂直,则实数的值为.2. 现有4个医疗小组和4个需要援助的国家,若每个医疗小组只去一个国家,且4个医疗小组去的国家各不相同,则不同的分配方法共有种.3. 已知是正方体棱的中点,则直线与平面所成的角的大小等于.4. 若函数 , 则 .5. 若 , 则正整数的值等于.6. 棱长都是3的三棱锥的高等于.7. 已知平面直角坐标系中的三点、、 , 若直线过点且与直线平行,则的方程为.8. 如图,在三棱锥中,平面 , , 则以此三棱锥的棱为边所构成的三角形中,直角三角形的个数有个.
 9. 从四棱锥的5个顶点中任选4个不同的点,则这四点能够构成不同三棱锥的个数是(结果用数字作答)10. 已知P为抛物线上一个动点,Q为圆上一个动点,那么点P到点Q的距离与点P到直线的距离之和的最小值是.11. 已知是等边三角形,、分别是边和的中点.若椭圆以、为焦点,且经过、 , 则椭圆的离心率等于.
9. 从四棱锥的5个顶点中任选4个不同的点,则这四点能够构成不同三棱锥的个数是(结果用数字作答)10. 已知P为抛物线上一个动点,Q为圆上一个动点,那么点P到点Q的距离与点P到直线的距离之和的最小值是.11. 已知是等边三角形,、分别是边和的中点.若椭圆以、为焦点,且经过、 , 则椭圆的离心率等于.二、单选题
-
12. 双曲线的两条渐近线的夹角等于( )A、 B、 C、 D、13. “ , ”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件14. 下列命题中正确的是( )A、终边重合的两个角相等 B、锐角是第一象限的角 C、第二象限的角是钝角 D、小于90°的角都是锐角15. 下列说法正确的是( )A、若 , 则与的长度相等且方向相同或相反; B、若 , 且与的方向相同,则 C、平面上所有单位向量,其终点在同一个圆上; D、若 , 则与方向相同或相反16. 已知为虚数单位,下列说法中错误的是( )A、复数对应的向量为 , 复数对应的向量为 , 若 , 则 B、互为共轭复数的两个复数的模相等,且 C、复数的模实质上就是复平面内复数对应的点到原点的距离,也就是复数对应的向量的模 D、若复数满足 , 则复数对应的点在以为圆心,为半径的圆上
三、解答题
-
17. 若:(1)、当时,求的值;(2)、求的值.18. 亭子是一种中国传统建筑,多建于园林,人们在欣赏美景的同时也能在亭子里休息、避雨、乘凉(如图1).假设我们把亭子看成由一个圆锥与一个圆柱构成的几何体(如图2).一般地,设圆锥中母线与底面所成角的大小为 , 当时,方能满足建筑要求.已知圆锥高为米,底面半径为米,圆柱高为3米,底面半径为2米.

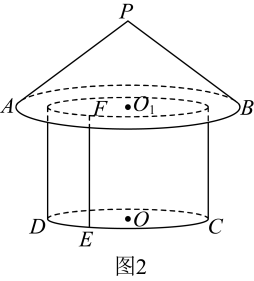 (1)、求几何体的体积;(2)、如图2,设为圆柱底面半圆弧的三等分点,求圆柱母线和圆锥母线所在异面直线所成角的大小,并判断该亭子是否满足建筑要求.19. 已知椭圆:的左、右焦点为 , , 点是椭圆的上顶点,经过的直线交椭圆于 , 两个不同的点.(1)、求点到直线的距离;(2)、若直线的斜率为 , 且 , 求实数的值.20. 如图所示的几何体中,四边形为正方形,.
(1)、求几何体的体积;(2)、如图2,设为圆柱底面半圆弧的三等分点,求圆柱母线和圆锥母线所在异面直线所成角的大小,并判断该亭子是否满足建筑要求.19. 已知椭圆:的左、右焦点为 , , 点是椭圆的上顶点,经过的直线交椭圆于 , 两个不同的点.(1)、求点到直线的距离;(2)、若直线的斜率为 , 且 , 求实数的值.20. 如图所示的几何体中,四边形为正方形,.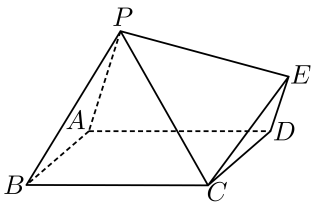 (1)、求证:∥平面;(2)、若 , , 平面平面.求平面与平面所成锐二面角的大小.21. 如图所示的几何体中,四边形为正方形,.
(1)、求证:∥平面;(2)、若 , , 平面平面.求平面与平面所成锐二面角的大小.21. 如图所示的几何体中,四边形为正方形,.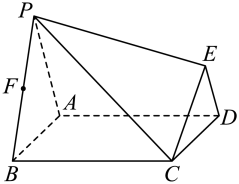 (1)、求证:平面;(2)、若 , 平面平面.若为中点,求证:.22. 如图,已知等腰直角三角形的两直角边 , 的边长为4,过边的等分点作边的垂线 , 过边的等分点和顶点作直线 , 记与的交点为.若以点为坐标原点,所在的直线为轴(点在轴的正半轴上),建立平面直角坐标系.
(1)、求证:平面;(2)、若 , 平面平面.若为中点,求证:.22. 如图,已知等腰直角三角形的两直角边 , 的边长为4,过边的等分点作边的垂线 , 过边的等分点和顶点作直线 , 记与的交点为.若以点为坐标原点,所在的直线为轴(点在轴的正半轴上),建立平面直角坐标系. (1)、证明:对任意的正整数 , 点都在抛物线:上;(2)、已知是抛物线:在第一象限的点,过点与抛物线相切的直线与轴的交点为.过点的直线与直线垂直,且与抛物线交于另一点.记的面积为 , 试用解析法将表示为的函数,并求的最小值.23. 如图,已知等腰直角三角形的两直角边 , 的边长为4,过边的等分点作边的垂线 , 过边的等分点和顶点作直线 , 记与的交点为.若以点为坐标原点,所在的直线为轴(点在轴的正半轴上),建立平面直角坐标系.
(1)、证明:对任意的正整数 , 点都在抛物线:上;(2)、已知是抛物线:在第一象限的点,过点与抛物线相切的直线与轴的交点为.过点的直线与直线垂直,且与抛物线交于另一点.记的面积为 , 试用解析法将表示为的函数,并求的最小值.23. 如图,已知等腰直角三角形的两直角边 , 的边长为4,过边的等分点作边的垂线 , 过边的等分点和顶点作直线 , 记与的交点为.若以点为坐标原点,所在的直线为轴(点在轴的正半轴上),建立平面直角坐标系.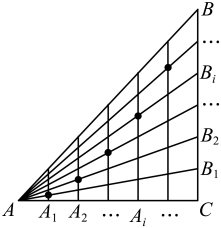 (1)、当时,求点的坐标;(2)、已知是抛物线:在第一象限的点,过点与抛物线相切的直线与轴的交点为.过点的直线与直线垂直,与抛物线交于另一点 , 且与轴交于点.若为等腰直角三角形,求的面积.
(1)、当时,求点的坐标;(2)、已知是抛物线:在第一象限的点,过点与抛物线相切的直线与轴的交点为.过点的直线与直线垂直,与抛物线交于另一点 , 且与轴交于点.若为等腰直角三角形,求的面积.