四川省资阳市2022-2023学年高一下学期期末数学试题
试卷更新日期:2023-08-24 类型:期末考试
一、单选题
-
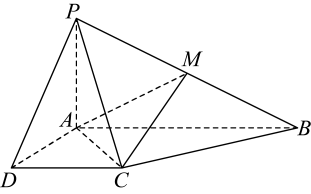
1. 复数( )A、 B、 C、 D、2. 数据1,2,3,4,5,6,7,8的分位数为( )A、4.5 B、5 C、5.5 D、63. 若角α是第二象限角,则是( )A、第一象限角 B、第二象限角 C、第一或第三象限角 D、第二或第四象限角4. 能使平面与平面平行的一个条件是( )A、与都平行于同一条直线 B、一条直线l分别与和所成的角相等 C、内有无数条直线都与平行 D、内的任何一条直线都与平行5. 的值为( )A、 B、 C、0 D、6. 在中,内角A , B , C的对边分别为a , b , c , 已知 , , , 则( )A、 B、 C、 D、为钝角三角形7. 三棱台中,两底面和分别是边长为2和1的等边三角形,平面ABC.若 , 则异面直线AC与所成角的余弦值为( )
 A、 B、 C、 D、8. 折扇又名“纸扇”是一种用竹木或象牙做扇骨、韧纸或者绫绢做扇面的能折叠的扇子.某折扇如图1所示,其平面图为如图2所示的扇形AOB , 其半径为3, , 点E , F分别在 , 上,且 , 则的取值范围是( )
A、 B、 C、 D、8. 折扇又名“纸扇”是一种用竹木或象牙做扇骨、韧纸或者绫绢做扇面的能折叠的扇子.某折扇如图1所示,其平面图为如图2所示的扇形AOB , 其半径为3, , 点E , F分别在 , 上,且 , 则的取值范围是( )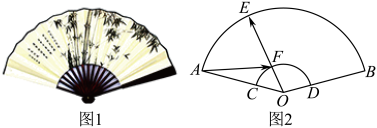 A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
9. 某运动员在一次射击训练中射靶10次,其命中环数依次为7,5,8,9,6,6,7,7,8,7,则该运动员射击成绩的( )A、众数为7 B、中位数为8 C、平均数为7 D、方差为10. 已知单位向量 , 满足 , 则以下结论正确的有( )A、 B、 C、向量 , 的夹角为 D、在上的投影向量为11. 已知函数的部分图象如图所示,下列说法正确的是( )
 A、 B、函数的图象关于直线对称 C、函数在上单调递增 D、将函数.的图象向左平移个单位后得到函数的图象,则为偶函数12. 如图,在正方体中,E是棱CD上的动点,则下列结论正确的是( )
A、 B、函数的图象关于直线对称 C、函数在上单调递增 D、将函数.的图象向左平移个单位后得到函数的图象,则为偶函数12. 如图,在正方体中,E是棱CD上的动点,则下列结论正确的是( )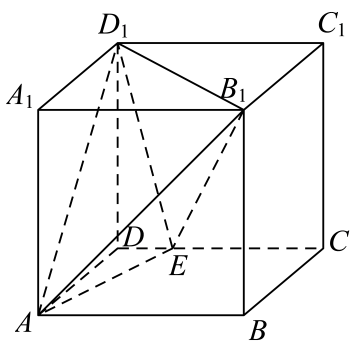 A、与所在的直线异面 B、 C、三棱锥的体积为定值 D、直线与平面所成角的正弦值为
A、与所在的直线异面 B、 C、三棱锥的体积为定值 D、直线与平面所成角的正弦值为三、填空题
-
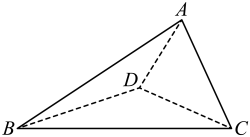
13. 某学校高中一年级有男生500人,女生400人,按性别进行分层,用分层抽样的方法从该年级学生中随机抽取一个容量为45的样本,则所抽取的女生人数为.14. 已知平面向量 , , .若 , 则x=.15. 复平面内复数 , 对应的两点之间的距离为.16. 如图,三棱锥中,平面平面BCD , 是边长为2的等边三角形, , .若A , B , C , D四点在某个球面上,则该球体的表面积为.
四、解答题
-
17. 已知复数 , , 其中i是虚数单位,.(1)、若为纯虚数,求m的值;(2)、若 , 求的虚部.18. 已知函数在区间上的最大值为1.(1)、求常数m的值;(2)、当时,求函数的最小值,以及相应x的集合.19. 为了解某市家庭用电量的情况,统计部门随机调查了200户居民去年一年的月均用电量(单位:),将全部数据按区间 , , …,分成8组,得到如下的频率分布直方图:
 (1)、求图中a的值;并估计这200户居民月用电量的平均值(同一组中的数据用该组区间的中点值为代表);(2)、为了既满足居民的基本用电需求,又提高能源的利用效率,市政府计划采用阶梯电价,使75%的居民缴费在第一档,20%的居民缴费在第二档,其余5%的居民缴费在第三档,试基于统计数据确定各档月均用电量的范围(计算百分位数时,结果四舍五入取整数).
(1)、求图中a的值;并估计这200户居民月用电量的平均值(同一组中的数据用该组区间的中点值为代表);(2)、为了既满足居民的基本用电需求,又提高能源的利用效率,市政府计划采用阶梯电价,使75%的居民缴费在第一档,20%的居民缴费在第二档,其余5%的居民缴费在第三档,试基于统计数据确定各档月均用电量的范围(计算百分位数时,结果四舍五入取整数).