四川省成都市2024届新高三上学期6月零诊模拟考试数学(文)试题
试卷更新日期:2023-08-24 类型:高考模拟
一、单选题:共12道小题,每题5分,共60分.
-
1. 直线:与直线:平行,则( )A、 B、 C、2 D、2. 设 , 则的虚部为( )A、 B、 C、1 D、33. 一组数据包括47、48、51、54、55,则这组数据的标准差为( )A、 B、 C、10 D、504. 已知函数在其定义域上的导函数为 , 当时,“”是“单调递增”的( )A、充要条件 B、既不充分也不必要条件 C、必要不充分条件 D、充分不必要条件5. 圆:与直线:的位置关系为( )A、相切 B、相交 C、相离 D、无法确定6. 如图所示的算法框图思路源于我国古代数学名著《九章算术》中的“更相减相术”,执行该算法框图,若输入的、分别为36、96,则输出的( )
 A、0 B、8 C、12 D、247. 直线与抛物线:交于、两点,若 , 其中为坐标原点,则的准线方程为( )A、 B、 C、 D、8. 函数的图象经过变换:后得到函数的图象,则( )A、 B、 C、 D、9. 有甲、乙、丙、丁四名学生参加歌唱比赛,其中只有一位获奖,有人走访了四人,甲说:“是乙或丙获奖.”乙说:“甲、丙都未获奖.”丙说:“我获奖了.”丁说:“是乙获奖.”四位歌手的话只有两句是对的,则获奖的歌手是( )A、甲 B、乙 C、丙 D、丁10. 点、在以为直径的球的表面上,且 , , 已知球的表面积是 , 下列说法中正确的个数是( )
A、0 B、8 C、12 D、247. 直线与抛物线:交于、两点,若 , 其中为坐标原点,则的准线方程为( )A、 B、 C、 D、8. 函数的图象经过变换:后得到函数的图象,则( )A、 B、 C、 D、9. 有甲、乙、丙、丁四名学生参加歌唱比赛,其中只有一位获奖,有人走访了四人,甲说:“是乙或丙获奖.”乙说:“甲、丙都未获奖.”丙说:“我获奖了.”丁说:“是乙获奖.”四位歌手的话只有两句是对的,则获奖的歌手是( )A、甲 B、乙 C、丙 D、丁10. 点、在以为直径的球的表面上,且 , , 已知球的表面积是 , 下列说法中正确的个数是( )①平面;②平面平面;③ .
A、0 B、1 C、2 D、311. 关于圆周率 , 数学史上出现过很多有创意的求法,如著名的浦丰实验和查理斯实验.受其启发,可通过设计如下实验来估计值:先请100名同学每人随机写下一组正实数对 , 且要求 , 均小于1;再统计、和1作为三边长能形成钝角三角形的数对的个数;最后利用统计结果估计值.假如某次实验结果得到 , 那么本次实验可以将值估计为( )A、 B、 C、 D、12. 函数零点个数为( )A、4 B、3 C、2 D、1二、填空题:共4道小题,每题5分,共20分.
-
13. 命题“ , ”的否定为 .14. 函数的图象在处的切线方程为 .15. 某区为了解全区12000名高二学生的体能素质情况,在全区高二学生中随机抽取了1000名学生进行体能测试,并将这1000名的体能测试成绩整理成如下频率分布直方图.根据此频率分布直方图,这1000名学生平均成绩的估计值为 .
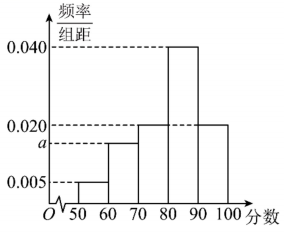 16. 双曲线:其左、右焦点分别为、 , 倾斜角为的直线与双曲线在第一象限交于点 , 设双曲线右顶点为 , 若 , 则双曲线的离心率的取值范围为 .
16. 双曲线:其左、右焦点分别为、 , 倾斜角为的直线与双曲线在第一象限交于点 , 设双曲线右顶点为 , 若 , 则双曲线的离心率的取值范围为 .三、解答题:共5道大题,共70分.
-
17. 设函数 ,(1)、求、的值;(2)、求在上的最值.18. 如图1,、、分别是边长为4的正方形的三边、、的中点,先沿着虚线段将等腰直角三角形裁掉,再将剩下的五边形沿着线段折起,连接、就得到了一个空间五面体,如图2.

 (1)、若是四边形对角线的交点,求证:平面;(2)、若 , 求三棱锥的体积.19. 信创产业即信息技术应用创新产业,是一条规模庞大、体系完整的产业链,是数字经济的重要抓手之一.在政府、企业等多方面的共同努力下,中国信创产业市场规模不断扩大,市场释放出前所未有的活力.下表为2018-2022年中国信创产业规模(单位:千亿元),其中2018-2022年对应的代码依次为1~5.
(1)、若是四边形对角线的交点,求证:平面;(2)、若 , 求三棱锥的体积.19. 信创产业即信息技术应用创新产业,是一条规模庞大、体系完整的产业链,是数字经济的重要抓手之一.在政府、企业等多方面的共同努力下,中国信创产业市场规模不断扩大,市场释放出前所未有的活力.下表为2018-2022年中国信创产业规模(单位:千亿元),其中2018-2022年对应的代码依次为1~5.年份代码
1
2
3
4
5
中国信创产业规模/千亿元
8.1
9.6
11.5
13.8
16.7
(1)、从2018-2022年中国信创产业规模中任取2个数据,求这2个数据都大于10的概率.(2)、由上表数据可知,可用指数型函数模型拟合与的关系,请建立关于的回归方程( , 的值精确到0.01),并预测2023年中国信创产业规模能否超过20千亿元.参考数据:
2.45
38.52
6.81
1.19
2.84
其中 , .
参考公式:对于一组数据 , , , , 其回归直线的斜率和截距的最小二乘估计公式分别为 , .
20. 椭圆:上顶点为 , 左焦点为 , 中心为 . 已知为轴上动点,直线与椭圆交于另一点;而为定点,坐标为 , 直线与轴交于点 . 当与重合时,有 , 且 .(1)、求椭圆的标准方程;(2)、设的横坐标为 , 且 , 当面积等于时,求的取值.