陕西省渭南市临渭区2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-08-24 类型:期末考试
一、单选题
-
1. 下列图形中,是轴对称图形的个数是( )
 A、1 B、2 C、3 D、42. 下列计算正确的是( )A、 B、 C、 D、3. 随着科技不断发展,芯片的集成度越来越高,我国企业中芯国际已经实现14纳米量产,14纳米 毫米,0.000014用科学记数法表示为( )A、 B、 C、 D、4. 若长度分别是a、3、5的三条线段能组成一个三角形,则a的值可以是( )A、1 B、2 C、4 D、85. 下列事件中的必然事件是( )A、任意买一张电影票,座位号是的倍数 B、打开电视机,它正在播放广告 C、明年月日渭南一定会下雨 D、早上的太阳从东方升起6. 如图,直线a∥b,△ABC的顶点C在直线b上,边AB与直线b相交于点D.若△BCD是等边三角形,∠A=20°,则∠1度数为( )
A、1 B、2 C、3 D、42. 下列计算正确的是( )A、 B、 C、 D、3. 随着科技不断发展,芯片的集成度越来越高,我国企业中芯国际已经实现14纳米量产,14纳米 毫米,0.000014用科学记数法表示为( )A、 B、 C、 D、4. 若长度分别是a、3、5的三条线段能组成一个三角形,则a的值可以是( )A、1 B、2 C、4 D、85. 下列事件中的必然事件是( )A、任意买一张电影票,座位号是的倍数 B、打开电视机,它正在播放广告 C、明年月日渭南一定会下雨 D、早上的太阳从东方升起6. 如图,直线a∥b,△ABC的顶点C在直线b上,边AB与直线b相交于点D.若△BCD是等边三角形,∠A=20°,则∠1度数为( ) A、∠1=20° B、∠1=60° C、∠1=40° D、无法判断7.
A、∠1=20° B、∠1=60° C、∠1=40° D、无法判断7.如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
 A、
A、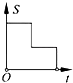 B、
B、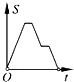 C、
C、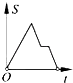 D、
D、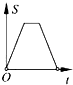 8. 在学习完“探索三角形全等的条件”一节后,一同学总结出很多全等三角形的模型,他设计了以下问题给同桌解决:如图,做一个“U”字形框架PABQ,其中AB=42cm,AP,BQ足够长,PA⊥AB于A,QB⊥AB于点B,点M从B出发向A运动,同时点N从B出发向Q运动,使M,N运动的速度之比3:4,当两点运动到某一瞬间同时停止,此时在射线AP上取点C,使△ACM与△BMN全等,则线段AC的长为( )
8. 在学习完“探索三角形全等的条件”一节后,一同学总结出很多全等三角形的模型,他设计了以下问题给同桌解决:如图,做一个“U”字形框架PABQ,其中AB=42cm,AP,BQ足够长,PA⊥AB于A,QB⊥AB于点B,点M从B出发向A运动,同时点N从B出发向Q运动,使M,N运动的速度之比3:4,当两点运动到某一瞬间同时停止,此时在射线AP上取点C,使△ACM与△BMN全等,则线段AC的长为( ) A、18cm B、24cm C、18cm或28cm D、18cm或24cm
A、18cm B、24cm C、18cm或28cm D、18cm或24cm二、填空题
-
9. 如果一个角等于 , 那么它余角的补角是 .10. 某农场引进一批新菜种,播种前在相同条件下进行发芽试验,结果如表所示:
试验的菜种数
500
1000
2000
10000
20000
发芽的频率
0.974
0.983
0.971
0.973
0.971
在与实验条件相同的情况下,估计种一粒这样的菜种发芽的概率为.(精确到0.01)
11. 已知 ,则m=.12. 如图,要把池中的水引到处,可过点作于 , 然后沿开渠,可使所开水渠长度最短,如此设计的数学原理是 .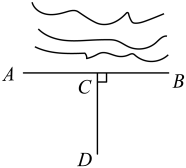 13. 如图,在△ABC中,AB=6,AC=9,EF垂直平分线段BC,P是直线EF上的任意一点,则△ABP周长的最小值是 .
13. 如图,在△ABC中,AB=6,AC=9,EF垂直平分线段BC,P是直线EF上的任意一点,则△ABP周长的最小值是 .
三、解答题
-
14. 计算: .15. 先化简,再求值: , 其中 , .16. 如图,在边长为1个单位长度的小正方形组成的6×8的网格中,给出了格点(顶点为网格线的交点)△ABC,l是过网格线的一条直线.

⑴求△ABC的面积;
⑵作△ABC关于直线l对称的图形△A′B′C′;
⑶在边BC上找一点D,连接AD,使得∠BAD=∠ABD.(保留作图痕迹)
17. 如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE. 18. 如图,点E、F在BD上,且 , , , 试说明:点O是AC的中点.请你在横线上补充其推理过程或理由.
18. 如图,点E、F在BD上,且 , , , 试说明:点O是AC的中点.请你在横线上补充其推理过程或理由.
解:因为
所以 , 即 ▲
因为 ,
所以 ▲ (理由:SSS)
所以(理由: )
因为(理由: )
所以(理由: )
所以 ▲ (理由:全等三角形对应边相等)
所以点O是AC的中点.
19. 如图,已知△ABC,∠C=90°,∠A=30°,用尺规作图法在AC上确定一点P,使PB+PC=AC.(不写作法,保留作图痕迹.) 20. 如图,长为25米,宽为12米的长方形地面上,修筑宽度均为m米的两条互相垂直的小路(图中阴影部分),其余部分作草地,如果将两条小路铺上地砖,选用地砖的价格是45元/平方米.
20. 如图,长为25米,宽为12米的长方形地面上,修筑宽度均为m米的两条互相垂直的小路(图中阴影部分),其余部分作草地,如果将两条小路铺上地砖,选用地砖的价格是45元/平方米. (1)、写出买地砖需要的费用y(元)与m(米)之间的关系式.(2)、计算当m=2时,买地砖需要的费用.21. 一个不透明的口袋中装有6个红球,9个黄球,3个白球,这些球除颜色外其他均相同.从中任意摸出一个球.(1)、求摸到的球是白球的概率.(2)、如果要使摸到白球的概率为 ,需要在这个口袋中再放入多少个白球?22. 一辆汽车油箱内有油56升,从某地出发,每行驶1千米,耗油0.08升,如果设油箱内剩油量为y(升),行驶路程为x(千米),则y随x的变化而变化.(1)、在上述变化过程中,自变量是 , 因变量是 .(2)、用表格表示汽车从出发地行驶100千米、200千米、300千米、400千米时的剩油量.请将表格补充完整:
(1)、写出买地砖需要的费用y(元)与m(米)之间的关系式.(2)、计算当m=2时,买地砖需要的费用.21. 一个不透明的口袋中装有6个红球,9个黄球,3个白球,这些球除颜色外其他均相同.从中任意摸出一个球.(1)、求摸到的球是白球的概率.(2)、如果要使摸到白球的概率为 ,需要在这个口袋中再放入多少个白球?22. 一辆汽车油箱内有油56升,从某地出发,每行驶1千米,耗油0.08升,如果设油箱内剩油量为y(升),行驶路程为x(千米),则y随x的变化而变化.(1)、在上述变化过程中,自变量是 , 因变量是 .(2)、用表格表示汽车从出发地行驶100千米、200千米、300千米、400千米时的剩油量.请将表格补充完整:行驶路程x(千米)
100
200
300
400
油箱内剩油量y(升)
40
24
(3)、试写出y与x的关系式是 .(4)、这辆汽车行驶350千米时,剩油量是多少?汽车油箱内剩油8升时,汽车行驶了多少千米?23. 如图,在△ABC中,D是BC边上的一点, , BE平分∠ABC,交AC边于点E,连接DE. (1)、试说明;(2)、若 , , 求∠DEC的度数.24. 如图,在中,垂直平分 , 交于点F,于点D, , 连接 .
(1)、试说明;(2)、若 , , 求∠DEC的度数.24. 如图,在中,垂直平分 , 交于点F,于点D, , 连接 . (1)、若平分 , 求的度数;(2)、若的周长为 , , 求的长.25. 如图
(1)、若平分 , 求的度数;(2)、若的周长为 , , 求的长.25. 如图 (1)、问题背景:如图 , 在四边形中, , , , , 分别是 , 上的点,且 , 探究图中线段 , , 之间的数量关系.小王同学探究此问题的方法是:延长到点 , 使 , 连接 , 先证明 , 再证明 , 可得出结论,他的结论应是, ▲ , 请说明理由;(2)、实际应用:如图 , 在新修的小区中,有块四边形绿化 , 四周修有步行小径,且 , , 在小径 , 上各修一凉亭 , , 在凉亭与之间有一池塘,不能直接到达.经测量得到 , 米,米,试求两凉亭之间的距离 .
(1)、问题背景:如图 , 在四边形中, , , , , 分别是 , 上的点,且 , 探究图中线段 , , 之间的数量关系.小王同学探究此问题的方法是:延长到点 , 使 , 连接 , 先证明 , 再证明 , 可得出结论,他的结论应是, ▲ , 请说明理由;(2)、实际应用:如图 , 在新修的小区中,有块四边形绿化 , 四周修有步行小径,且 , , 在小径 , 上各修一凉亭 , , 在凉亭与之间有一池塘,不能直接到达.经测量得到 , 米,米,试求两凉亭之间的距离 .