陕西省渭南市蒲城县2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-24 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若 , 则下列不等式正确的是( )A、 B、 C、 D、3. 若一个多边形的每一个外角都等于 , 则这个多边形的边数是( )A、9 B、10 C、7 D、84. 下列各式从左到右的变形中,属于因式分解的是( )A、 B、 C、 D、5. 下面给出四边形中,、、、的度数之比,其中能判定四边形是平行四边形的是( )A、 B、 C、 D、6. 如图,在△ABC中,BC=1,AB=3, , D为AC上一点,连接BD,若 , 则的度数为( )
2. 若 , 则下列不等式正确的是( )A、 B、 C、 D、3. 若一个多边形的每一个外角都等于 , 则这个多边形的边数是( )A、9 B、10 C、7 D、84. 下列各式从左到右的变形中,属于因式分解的是( )A、 B、 C、 D、5. 下面给出四边形中,、、、的度数之比,其中能判定四边形是平行四边形的是( )A、 B、 C、 D、6. 如图,在△ABC中,BC=1,AB=3, , D为AC上一点,连接BD,若 , 则的度数为( )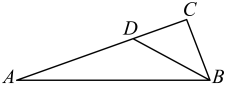 A、40° B、35° C、30° D、20°7. 若关于的分式方程有增根,则的值为( )A、 B、3 C、2 D、8. 如图、在平行四边形中, , , 平分 , 对角线、相交下点 , 连接 , 下列结论:①;②;③;④ . 其中正确的有( )
A、40° B、35° C、30° D、20°7. 若关于的分式方程有增根,则的值为( )A、 B、3 C、2 D、8. 如图、在平行四边形中, , , 平分 , 对角线、相交下点 , 连接 , 下列结论:①;②;③;④ . 其中正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 若分式的值为0,则 .10. 因式分解: .11. 函数与的图像如图所示,根据图像可知不等式的解集是 .
 12. 如图,在平面直角坐标系中,四边形是平行四边形, , , 轴,则的长为 .
12. 如图,在平面直角坐标系中,四边形是平行四边形, , , 轴,则的长为 . 13. 如图,在中, , , 是的中点, , 垂足为点 , 是的中点,连接 , 过点作的垂线交的延长线于点 , 若 , 则的长为 .
13. 如图,在中, , , 是的中点, , 垂足为点 , 是的中点,连接 , 过点作的垂线交的延长线于点 , 若 , 则的长为 .
三、解答题
-
14. 分解因式: .15. 解方程: .16. 如图,在中,请用尺规作图法在边上找一点 , 连接 , 使得.(保留作图痕迹,不写作法)
 17. 如图,在△ABC中,AD平分∠BAC,点E在BA的延长线上,且EC∥AD.证明:△ACE是等腰三角形.
17. 如图,在△ABC中,AD平分∠BAC,点E在BA的延长线上,且EC∥AD.证明:△ACE是等腰三角形. 18. 如图,四边形对角线交于点 , 且为中点,点、在直线上, , . 求证:四边形是平行四边形.
18. 如图,四边形对角线交于点 , 且为中点,点、在直线上, , . 求证:四边形是平行四边形. 19. 解不等式组: , 并把解集在数轴上表示出来.
19. 解不等式组: , 并把解集在数轴上表示出来. 20. 先化简,再求值: , 其中a=2023.21. 如图,方格纸中每个小正方形的边长都是1个单位长度,建立平面直角坐标系,的三个顶点坐标分别为 , , .
20. 先化简,再求值: , 其中a=2023.21. 如图,方格纸中每个小正方形的边长都是1个单位长度,建立平面直角坐标系,的三个顶点坐标分别为 , , .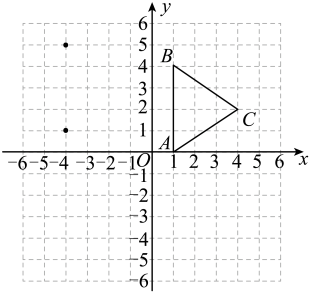 (1)、将向左平移5个单位,再向上平移1个单位,画出平移后的;(2)、画出将绕原点按顺时针方向旋转后的 , 并写出点的对应点的坐标.22. 常用的因式分解的方法有:提公因式法和公式法,但有的多项式用上述方法无法分解,例如 ,我们细心观察就会发现,前两项可以分解,后两项也可以分解,分别分解后会产生公因式就可以完整的分解了,具体分解过程如下:
(1)、将向左平移5个单位,再向上平移1个单位,画出平移后的;(2)、画出将绕原点按顺时针方向旋转后的 , 并写出点的对应点的坐标.22. 常用的因式分解的方法有:提公因式法和公式法,但有的多项式用上述方法无法分解,例如 ,我们细心观察就会发现,前两项可以分解,后两项也可以分解,分别分解后会产生公因式就可以完整的分解了,具体分解过程如下:这种方法叫分组分解法,请利用这种方法因式分解下列多项式:
(1)、 ;(2)、 .23. 如图,在中, , 平分 , 交平点 , 且 , 过作交于点 . 求证: (1)、是等边三角形;(2)、点是的中点.24. 如图,在中,点E在上,点F在上,且 .
(1)、是等边三角形;(2)、点是的中点.24. 如图,在中,点E在上,点F在上,且 .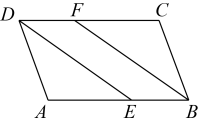 (1)、求证:四边形是平行四边形;(2)、若为的平分线,且 , , 求的周长.25. 生态优先,绿色发展,让美丽的地球添上更多“中国绿”.某小区为抓好“园区绿化”,购买了甲、乙两种树苗,购买甲种树苗花了1200元,购买乙种树苗花了900元,甲种树苗的单价是乙种树苗的倍,购买甲种树苗的数量比购买乙种树苗的数量少10棵.(1)、求甲、乙两种树苗单价分别是多少元?(2)、为扩大园区绿化面积,该小区准备再次购进甲、乙两种树苗共100棵,若总金额不超过1314元,问最少购进多少棵乙种树苗?26. 如图
(1)、求证:四边形是平行四边形;(2)、若为的平分线,且 , , 求的周长.25. 生态优先,绿色发展,让美丽的地球添上更多“中国绿”.某小区为抓好“园区绿化”,购买了甲、乙两种树苗,购买甲种树苗花了1200元,购买乙种树苗花了900元,甲种树苗的单价是乙种树苗的倍,购买甲种树苗的数量比购买乙种树苗的数量少10棵.(1)、求甲、乙两种树苗单价分别是多少元?(2)、为扩大园区绿化面积,该小区准备再次购进甲、乙两种树苗共100棵,若总金额不超过1314元,问最少购进多少棵乙种树苗?26. 如图
【操作】
如图1,是等腰直角三角形, , 是其内部的一点,连接 . 将绕点顺时针旋转90°得到 , 连接、 , 作直线交于点 .
(1)、求证:;(2)、设与交于点 , 求的度数;(3)、【探究】
如图2,连接图1中的 , 分别取、、的中点、、 , 作 . 若 , 求的周长.