陕西省渭南市大荔县2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-08-24 类型:期末考试
一、单选题
-
1. 如图,数轴上雪容融所在点表示的数可能为( )
 A、3 B、1 C、 D、2. 计算的结果为( )A、 B、 C、 D、23. 下列各选项中能用“垂线段最短”来解释的现象是( )A、
A、3 B、1 C、 D、2. 计算的结果为( )A、 B、 C、 D、23. 下列各选项中能用“垂线段最短”来解释的现象是( )A、 B、
B、 C、
C、 D、
D、 4. 根据下列表述,能确定具体位置的是( )A、钟楼北偏东 , 320米处 B、文投影院3号厅2排 C、北纬 D、渭南市西岳路5. 如图,请你观察,最接近( )
4. 根据下列表述,能确定具体位置的是( )A、钟楼北偏东 , 320米处 B、文投影院3号厅2排 C、北纬 D、渭南市西岳路5. 如图,请你观察,最接近( )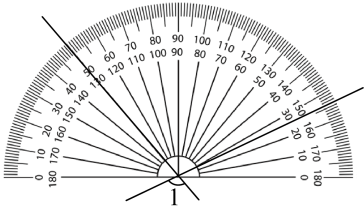 A、 B、 C、 D、6. 用代入法解方程组 时,代入正确的是( )A、x-2-x=4 B、x-2-2x=4 C、x-2+2x=4 D、x-2+x=47. 如图是一款手推车的平面示意图,其中 , , , 则的度数为( )
A、 B、 C、 D、6. 用代入法解方程组 时,代入正确的是( )A、x-2-x=4 B、x-2-2x=4 C、x-2+2x=4 D、x-2+x=47. 如图是一款手推车的平面示意图,其中 , , , 则的度数为( )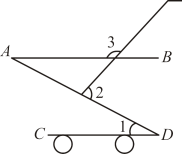 A、 B、 C、 D、8. 小红每分钟踢毽子的次数正常范围为少于80次,但不少于50次,用不等式表示为( )A、50<x<80 B、50≤x≤80 C、50≤x<80 D、50<x≤80
A、 B、 C、 D、8. 小红每分钟踢毽子的次数正常范围为少于80次,但不少于50次,用不等式表示为( )A、50<x<80 B、50≤x≤80 C、50≤x<80 D、50<x≤80二、填空题
-
9. 计算: .10. “5的算术平方根”这句话用数学符号表示为 .11. 调查大荔县居民的垃圾分类情况应采用(填“普查”或“抽样调查”)12. 某品牌电热水壶的进价为每个200元,以每个300元的标价山售.“五一节”期间,商店为让利于顾客,准备打折销售,但要保证利润率不低于 , 则最低可按标价的折出售.
 13. 如图,根据图中给出的数据,判断第一个图形的周长与第二个图形的周长的关系: . (填“等于”或“大于”或“小于”或“无法判断”).
13. 如图,根据图中给出的数据,判断第一个图形的周长与第二个图形的周长的关系: . (填“等于”或“大于”或“小于”或“无法判断”).
三、解答题
-
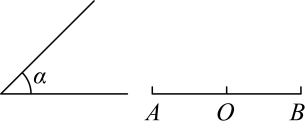
14.15. (用加减消元法).16. 已知 , 求代数式的值.17. 如图,已知锐角和平角 , 在内部求作 , 使与互补.(不要求尺规作图)
 18. 中国清代学者华衡芳和英国人傅兰雅合译英国瓦里斯的《代数学》,卷首有“代数之头,无论何数,皆可以任何记号代之”,说明了所谓“代数”,就是和符号来代表数的一种方法,若一个正数的平方根分别是和 , 求这个正数.19. 如图,数轴上点O为原点,点A,B,C表示的数分别是 .
18. 中国清代学者华衡芳和英国人傅兰雅合译英国瓦里斯的《代数学》,卷首有“代数之头,无论何数,皆可以任何记号代之”,说明了所谓“代数”,就是和符号来代表数的一种方法,若一个正数的平方根分别是和 , 求这个正数.19. 如图,数轴上点O为原点,点A,B,C表示的数分别是 . (1)、(用含m的代数式表示);(2)、求当与的差不小时,m的最小整数值.20. 用火柴棒按图中的方式搭图形.如图所示:
(1)、(用含m的代数式表示);(2)、求当与的差不小时,m的最小整数值.20. 用火柴棒按图中的方式搭图形.如图所示:
图形标号
①
②
③
④
⑤
…
火柴棒根数
5
9
13
17
…
(1)、根据规律填空:;(2)、按照这种方式搭下去,搭第n个图形需要火柴棒的根数为;(含n的式了表示)(3)、按这种方式搭下去,用(2)中的式子求第多少个图形需要4045根火柴?21. 如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.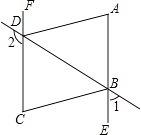 (1)、AE与FC会平行吗?说明理由;(2)、AD与BC的位置关系如何?为什么?(3)、BC平分∠DBE吗?为什么.22. 2022年3月23日,“天宫课堂”第二课开讲.“太空教师”翟志刚、王亚平、叶光富在中国空间站为广大青少年又一次带来了精彩的太空科普课.为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分为如下5组(满分100分),其中A组:75≤x<80,B组:80≤x<85,C组:85≤x<90,D组:90≤x<95,E组:95≤x<100,并绘制了如下不完整的统计图.
(1)、AE与FC会平行吗?说明理由;(2)、AD与BC的位置关系如何?为什么?(3)、BC平分∠DBE吗?为什么.22. 2022年3月23日,“天宫课堂”第二课开讲.“太空教师”翟志刚、王亚平、叶光富在中国空间站为广大青少年又一次带来了精彩的太空科普课.为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分为如下5组(满分100分),其中A组:75≤x<80,B组:80≤x<85,C组:85≤x<90,D组:90≤x<95,E组:95≤x<100,并绘制了如下不完整的统计图. (1)、本次调查一共随机抽取了名学生的成绩,频数分布直方图中m= , 扇形统计图中A组占%;(2)、补全学生成绩频数分布直方图;(3)、若将竞赛成绩在90分及以上的记为优秀,求优秀学生所在扇形对应圆心角的度数.23. 小开到早餐店买早点,下面是他和店主阿姨的对话小开说:“阿姨,我买个肉包和根油条”阿姨说:“一共元角”付款后,小开说:“阿姨,这根油条不要了,换个肉包吧阿姨说:“可以,但还需补交元钱”从他们的对话中你能知道肉包和油条的单价吗?24. 在平面直角坐标系中,若点的坐标满足 , 则我们称点N为“健康点”;若点的坐标满足 , 则我们称Q为“快乐点”.
(1)、本次调查一共随机抽取了名学生的成绩,频数分布直方图中m= , 扇形统计图中A组占%;(2)、补全学生成绩频数分布直方图;(3)、若将竞赛成绩在90分及以上的记为优秀,求优秀学生所在扇形对应圆心角的度数.23. 小开到早餐店买早点,下面是他和店主阿姨的对话小开说:“阿姨,我买个肉包和根油条”阿姨说:“一共元角”付款后,小开说:“阿姨,这根油条不要了,换个肉包吧阿姨说:“可以,但还需补交元钱”从他们的对话中你能知道肉包和油条的单价吗?24. 在平面直角坐标系中,若点的坐标满足 , 则我们称点N为“健康点”;若点的坐标满足 , 则我们称Q为“快乐点”. (1)、若点是“健康点”,则点A的坐标为 .(2)、在(1)的条件下,若点B是x轴上的“健康点”,点C是y轴上的“快乐点”,如果P为x轴上一点,且与面积相等,求点P的坐标.25. 根据下列证明过程填空:
(1)、若点是“健康点”,则点A的坐标为 .(2)、在(1)的条件下,若点B是x轴上的“健康点”,点C是y轴上的“快乐点”,如果P为x轴上一点,且与面积相等,求点P的坐标.25. 根据下列证明过程填空:如图, , 点在直线上,点、在直线上,且 , 点在线段上,连接 , 且平分 .

求证: .
证明:(已知),
( ),
▲ ,
(平角的定义),
,
平分(已知),
▲ ( ),
( ),
( ),
▲ ( ),
(等量代换).
26. 我们将内角互为对顶角的两个三角形称为“对顶二角形”.例如,在图1中,的内角与的内角为对顶角,则与为“对顶三角形”,根据三角形三个内角和是 , “对顶三角形”有如下性质: . (1)、性质理解:
(1)、性质理解:如图1,在“对顶三角形”与中,则 , 则 .
(2)、性质应用:如图2,在中,分别平分和 , 若 , 比大8°,求的度数.
(3)、拓展提高:如图3,是的角平分线,且和的平分线和相交于点P,设 , 请尝试求出的度数(用含的式了表示).