陕西省渭南市大荔县2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列等式成立的是（）．

A、 $\sqrt{16} = \pm 4$ B、 $\sqrt{{(- 2)}^{2}} = - 2$ C、 $\sqrt{\frac{1}{16}} = \frac{1}{8}$ D、 $\sqrt[3]{- 8} = - 2$

查看试题解析
2. 已知点P（m ， n）在第二象限，则直线y=nx＋m图象大致是下列的（）

A、 B、 C、 D、

查看试题解析
3. 添加下列一个条件，能使矩形 $A B C D$ 成为正方形的是（）

A、 $A B = C D$ B、 $A C ⊥ B D$ C、 $∠ B A D = 90 °$ D、 $A C = B D$

查看试题解析
4. 将直线 $y = - 2 x - 1$ 向右平移3个单位长度得到的直线不经过（）

A、第四象限 B、第三象限 C、第二象限 D、第一象限

查看试题解析
5. 如图，平行四边形 $A B C D$ 的周长为30， $A D ： A B = 3 ： 2$ ，那么 $B C$ 的长度是（）

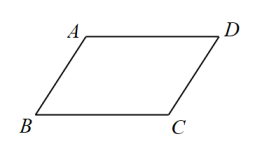A、9 B、12 C、15 D、18

查看试题解析
6. 为迎接亚运，某校购买了一批篮球和足球，已知购买足球的数量是篮球的2倍，购买足球用了5000元，购买篮球用了4000 元，篮球单价比足球贵30元.根据题意可列方程 $\frac{5000}{x} = 2 \times \frac{4000}{30 + x}$ ，则方程中x表示（）

A、篮球的数量 B、篮球的单价 C、足球的数量 D、足球的单价

查看试题解析
7. 如图，若点A在y轴上，点B在x轴上， $∠ O A B$ 的平分线交 $△ O A B$ 外角 $∠ O B D$ 的平分线于点C，则 $∠ C$ 的度数是（）

A、 $30 °$ B、 $45 °$ C、 $50 °$ D、 $60 °$

查看试题解析
8. 从甲，乙，丙，丁四人中选一人参加区里举办的垃圾分类知识大赛，经过三轮初赛，他们的平均成绩都是92.5分，方差分别是 ${s_{甲}}^{2} = 3.4$ ， ${s_{乙}}^{2} = 2.1$ ， ${s_{丙}}^{2} = 2.5$ ， ${s_{丁}}^{2} = 2.7$ ．你认为最合适的选手是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

二、填空题

9. $\sqrt{x} + 1$ 的一个有理化因式是．

查看试题解析
10. 如图，矩形内有两个相邻的正方形，面积分别是 $x^{2} (x > 2)$ 和4，那么阴影部分的面积．（用含x的代数式表示）

查看试题解析
11. 已知x，y为等腰三角形的两条边长，且x，y满足 $y = \sqrt{2 - x} + \sqrt{3 x - 6} + 3$ ，则此三角形的周长为．

查看试题解析
12. 对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形 $A B C D$ ，对角线 $A C$ ， $B D$ 交于点O．若 $A D = 2$ ， $B C = 5$ ，则 $A B^{2} + C D^{2} =$ ．

查看试题解析
13. 在菱形 $A B C D$ 中， $A B = 4$ ， $∠ B = 2 ∠ A$ ，点E，F分别是 $A D ， A B$ 的中点，动点P从B出发，沿着顺时针方向运动到C点，当 $△ P E F$ 为直角三角形时， $F P$ 的长度为．

查看试题解析

三、解答题

14. 计算： $2 \sqrt{3} - (3 \sqrt{2} + \sqrt{3})$

查看试题解析
15. 计算： $\sqrt[3]{- 8} + | 2 - \sqrt{5} | + {(1 - \sqrt{3})}^{0} + 4 \times \frac{\sqrt{5}}{2}$

查看试题解析
16. 化简 $\frac{x}{x + 1} - \frac{3 x}{2 (x + 1)} - 1$ 圆圆的解答过程如下：
解： $\frac{x}{x + 1} - \frac{3 x}{2 (x + 1)} - 1 = 2 x - 3 x - 1 = - 5 x - 1$
圆圆的解答正确吗？如果不正确，写出正确的解答．

查看试题解析
17. 如图，四边形ABCD是矩形，用直尺和圆规作出∠A的平分线与BC边的垂直平分线的交点Q（不写作法，保留作图痕迹）．连接QD，在新图形中，你发现了什么？请写出一条．

查看试题解析
18. “三农”问题是关系国计民生的根本问题，实施乡村振兴战略是建设美丽中国的关键举措．如图，某村有一块三角形空地 $A B C$ ，现计划将这块三角形空地进行新的规划，点D是 $B C$ 边上的一点，过点D作垂直于 $A C$ 的小路 $D E$ ．经测量， $A B = 13$ 米， $A D = 12$ 米， $A C = 15$ 米， $B D = 5$ 米．

(1)、求 $D C$ 的长；

(2)、求小路 $D E$ 的长．

查看试题解析
19. 2022午3月25日，教育部印发《义务教育课程方案和课程标准（2022年版）》，优化了课程设置，将劳动从综合实践活动课程中独立出来．某校为了解该校学生一周的课外劳动情况，随机抽取部分学生调查了他们一周的课外劳动时间，将数据进行整理并制成如一统计图．

请根据图中提供的信息，解答下向的问题：

(1)、求图1中的 $m =$ ，本次调查数据的中位数是 $h$ ，本次调查数据的众数是h；

(2)、若该校共有2000名学生，请根据统计数据，估计该校学生一周的课外劳动时间不小于3h的人数．

查看试题解析
20. 看着冉冉升起的五星红旗，你们是否想过旗杆到底有多高呢？某数学兴趣小组为了测量旗杆高度，进行以下操作：如图1，先将升旗的绳子拉到旗杆底端，发现绳子末端刚好接触到地面；如图2，再将绳子末端拉到距离旗杆8m处，发现绳子末端距离地面2m．请根据以上测量情况，计算旗杆的高度．

查看试题解析
21. 如图所示是个骑车者与一个跑步者的 $s$ 与t的图象，从图象中能够获得的合理信息有：（写出两条）

查看试题解析
22. 已知：如图，在 $▱ A B C D$ 中，点 $E ， F$ 分别在 $A D ， B C$ 上， $B E$ 平分 $∠ A B C$ ．请从以下三个条件：① $A E = B F$ ；② $A B = E F$ ；③ $A B ∥ E F$ 中，选择一个合适的条件，使四边形 $A B F E$ 为菱形．

(1)、你添加的条件是（填序号）；

(2)、添加了条件后，请证明四边形 $A B F E$ 为菱形．

查看试题解析
23. 2022年11月30日7时33分，神舟十五号3名航天员顺利进驻天宫空间站，与神舟十四号航天员乘组首次实现“太空会师”．某航模店看准商机，推出了“长征火箭”和“天宫空间站”两款模型．已知每个“天宫”模型的成本比“火箭”模型多10元，花费150元购进火箭模型的数量与花费250元购进天宫模型的数量一样多．

(1)、每个“火箭”模型和“天宫”模型的成本价各是多少元？

(2)、航模店计划购买两种模型共200个，其中“天宫”模型售价为40元，“火箭”模型的售价为20元．设购买“天宫”模型m个，销售批模型的利润为 $w$ 元．
①求 $w$ 与m的函数关系式（不要求写出m的取值范围）；
②若购进“天宫”模型的数量不超过“火箭”模型数量的 $\frac{1}{3}$ ，则购进“天宫”模型多少个时，售完这批模型可以获得最大利润？最大利润是多少？

查看试题解析
24. 如图①所示，平行四边形 $A B C D$ 是某公园的平面示意图． $A$ 、 $B$ 、 $C$ 、 $D$ 分别是该公园的四个入口，两条主干道 $A C$ 、 $B D$ 交于点 $O$ ，请你帮助公园的管理人员解决以下问题：

(1)、若 $A B = 1 k m$ ， $A C = 2.6 k m$ ， $B D = 2 k m$ ，公园的面积为 $k m^{2}$ ；

(2)、在（1）的条件下，如图②，公园管理人员在参观了南湖绿道后，为提升游客游览的体验感，准备修建三条绿道 $A N$ 、 $M N$ 、 $C M$ ，其中点 $M$ 在 $O B$ 上，点 $N$ 在 $O D$ 上，且 $B M = O N$ （点 $M$ 与点 $O$ 、 $B$ 不重合），并计划在 $△ A O N$ 与 $△ C O M$ 两块绿地所在区域种植郁金香，求种郁金香区域的面积；

(3)、若将公园扩大，此时 $A B = 2 k m$ ， $A C = 4 k m$ ， $B D = 4 k m$ ，修建（2）中的绿道每千米费用为 $10$ 万元，请你计算该公园修建这三条绿道投入资金的是小值．

查看试题解析