陕西省西安市莲湖区2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列数学曲线中（不含x，y轴），是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列条件中，能判断四边形 $A B C D$ 是平行四边形的是（）

A、 $A B / / C D ， A D = B C$ B、 $∠ A = ∠ B ， ∠ C = ∠ D$ C、 $A B = A D ， C B = C D$ D、 $A B / / C D ， A B = C D$

查看试题解析
3. 下列从左边到右边的变形中，是因式分解的是（）

A、 $x^{2} + 3 x + 1 = x (x + 3 + \frac{1}{x})$ B、 $(x - y)^{2} = x^{2} - 2 x y + y^{2}$ C、 $x^{2} - 1 + 4 k = (x + 1) (x - 1) + 4 k$ D、 $a^{2} - 9 = (a - 3) (a + 3)$

查看试题解析
4. 过多边形一个顶点的所有对角线把这个多边形分成了7个三角形，则这个多边形的边数是（）

A、8 B、9 C、10 D、11

查看试题解析
5. 若 $x > y$ 成立，则下列不等式成立的是（）

A、 $2 x - 1 > 2 y - 1$ B、 $- x + 1 > - y + 1$ C、 $\frac{x}{2} < \frac{y}{2}$ D、 $- x > - y$

查看试题解析
6. 如图，将 $△ A B C$ 沿 $B C$ 方向平移得到 $△ A^{'} B^{'} C^{'}$ ．连接 $A A^{'}$ ，若 $A A^{'} = 2.5 c m$ ， $B C^{'} = 10 c m$ ，则 $B^{'} C$ 的长为（）

A、 $3 c m$ B、 $4 c m$ C、 $5 c m$ D、 $6 c m$

查看试题解析
7. 如图，将 $△ A B C$ 绕点 $A$ 顺时针旋转 $120 °$ 得到 $△ A B^{'} C^{'}$ ，若点 $C ， B ， C^{'}$ 共线，则 $∠ B^{'} C^{'} C$ 的度数为（）

A、 $60 °$ B、 $45 °$ C、 $30 °$ D、 $15 °$

查看试题解析
8. 如图，直线 $y = k x + b$ 交坐标轴于 $A (- 2 ， 0) ， B (0 ， 1)$ 两点，则不等式 $- k x - b > 0$ 的解集为（）

A、 $x > - 2$ B、 $x < - 2$ C、 $x > 2$ D、 $x < 2$

查看试题解析

二、填空题

9. 若分式 $\frac{x - 2}{2 x + 1}$ 的值为0，那么x的值为．

查看试题解析
10. 若点 $P$ 与点 $Q (2 ， - 3)$ 关于坐标原点成中心对称，则点 $P$ 的坐标是．

查看试题解析
11. 已知关于 $x$ 的不等式 $x - m > - 3$ 的解集如图所示，则 $m$ 的值为．

查看试题解析
12. 如图，在 $▱ A B C D$ 中， $B D = 4 ， ∠ C = ∠ A B D$ ，则 $A D$ 的长为．

查看试题解析
13. 在 $Rt △ A B C$ 中， $∠ C = 90 ° ， A C = 6 ， B C = 8$ ，点N是 $B C$ 边上一点，点M为 $A B$ 边上的动点，点D、E分别为 $C N ， M N$ 的中点，则 $D E$ 的最小值是．

查看试题解析

三、解答题

14. 分解因式： $2 m^{3} n - 18 m n$ ．

查看试题解析
15. 解不等式组： ${\begin{array}{l} 2 x - 5 \leq 3 \\ 2 x - 1 > x + 1 \end{array}$ ．

查看试题解析
16. 化简： $(m + \frac{2 m + 1}{m}) \div \frac{m + 1}{m^{2}}$ ．

查看试题解析
17. 如图，在 $△ A B C$ 中，在 $B C$ 上找一点 $E$ ，连接 $A E$ ，使 $∠ B E A = 2 ∠ C$ ．（保留作图痕迹，不写作法）

查看试题解析
18. 如图， $A C$ 与 $B D$ 相交于点O， $D A ⊥ A C$ ， $D B ⊥ B C$ ， $A C = B D$ ．说明 $O D = O C$ 成立的理由．

查看试题解析
19. 如图，在平面直角坐标系中，已知点 $A (- 2 ， 2) ， B (- 3 ， 6) ， C (- 5 ， 3)$ ．

(1)、将 $△ A B C$ 沿着 $x$ 轴的方向平移得到 $△ A_{1} B_{1} C_{1}$ ，当点 $C$ 的对应点 $C_{1}$ 落在 $y$ 轴上时，画出 $△ A_{1} B_{1} C_{1}$ 的图形．

(2)、将 $△ A_{1} B_{1} C_{1}$ 原点 $O$ 顺时针旋转 $90 °$ 后，点 $A_{1}$ 的对应点 $A_{2}$ 的坐标是．

查看试题解析
20. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A B = 8$ ， $A D$ 是 $△ A B C$ 的一条角平分线．若 $C D = 2.5$ ，求 $△ A B D$ 的面积．

查看试题解析
21. 又是一年端阳至，绿杨带雨垂垂重，五色新丝缠角粽．端午节前夕，某超市打算用不超过3000元购买A，B两种品牌的粽子50盒，其中A种品牌粽子的单价是56元，B种品牌粽子的单价是64元，且购买B种品牌的粽子不少于23盒，请你求出所有购买方案．

查看试题解析
22. 已知一个正多边形的边数为n．

(1)、若这个多边形的内角和为其外角和的4倍，求n的值．

(2)、若这个正多边形的一个内角为 $108 °$ ，求n的值，

查看试题解析
23. 阅读下列材料，并解答相应问题：
对于二次三项式 $x^{2} + 2 a x + a^{2}$ 这样的完全平方式，可以用公式法将它分解成 $(x + a)^{2}$ 的形式，但是对于一般的二次三项式，就不能直接应用完全平方公式了，我们可以在二次三项式中先加上一项，使其配成完全平方式，再减去这项，使整个式子的值不变，例如： $x^{2} + 2 a x - 3 a^{2} = x^{2} + 2 a x + a^{2} - a^{2} - 3 a^{2} = (x + a)^{2} - (2 a)^{2} =$ ____．

(1)、用平方差公式补全上面算式最后一步．

(2)、用上述方法把 $m^{2} + 6 m + 8$ 分解因式．

查看试题解析
24. 如图，在四边形 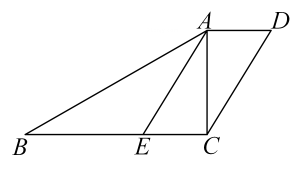$A B C D$ 中， $∠ A C B = ∠ C A D = 90 °$ ，点 $E$ 在 $B C$ 上， $A E ∥ D C$ ．

(1)、求证：四边形 $A E C D$ 是平行四边形．

(2)、若 $∠ B = 30 ° ， A E$ 平分 $∠ B A C ， A D = 2$ ，求四边形 $A E C D$ 的面积．

查看试题解析
25. 某药品生产车间为提高生产效益引进了新的设备，每台新设备每小时包装速度是旧设备包装速度的5倍．经过测试，用1台新设备包装1600盒药品的时间，比4台旧设备包装同样数量的药品节省4小时．

(1)、求一台新设备每小时可以包装多少盒药品．

(2)、该车间为了每小时完成不少于1000盒药品包装的任务量，决定同时使用新旧两种设备共18台，并且同时开始生产产品，那么至少需要新设备多少台？

查看试题解析
26. 如图

问题提出

(1)、如图1， $A D$ 是 $△ A B C$ 高，且 $B D = C D$ ，则 $△ A B C$ 是三角形．

(2)、问题探究
如图2，在 $▱ A B C D$ 中， $E$ 是 $A D$ 的中点，延长 $B E$ 交 $C D$ 的延长线于点 $F$ ．求证： $△ A E B ≌ △ D E F$ ．

(3)、问题解决
如图3，现有一块 $▱ A B C D$ 型板材， $E$ 为 $B C$ 边上的中点，工人师傅要在这块板材开出一个 $△ D E F$ 型凹槽，并要求 $∠ E F B + ∠ C D E = 90 °$ ，若 $D F = 13 ， A F = 3$ ，求 $B F$ 的长度．

查看试题解析