陕西省西安市莲湖区2022-2023学年七年级下学期末数学试题
试卷更新日期:2023-08-24 类型:期末考试
一、单选题
-
1. 下列字母是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算正确的是( )A、 B、 C、 D、3. 下列各组线段,能组成三角形的是( )A、1,3,5 B、1,5,6 C、2,3,5 D、2,5,64. 已知直线 , 一个直角三角板按如图方式放置,则∠1=( )
2. 下列运算正确的是( )A、 B、 C、 D、3. 下列各组线段,能组成三角形的是( )A、1,3,5 B、1,5,6 C、2,3,5 D、2,5,64. 已知直线 , 一个直角三角板按如图方式放置,则∠1=( ) A、 B、 C、 D、5. 从某郁金香种子中抽取7批,在同一条件下进行发芽试验,有关数据如下表:
A、 B、 C、 D、5. 从某郁金香种子中抽取7批,在同一条件下进行发芽试验,有关数据如下表:种子粒数
100
300
500
700
1000
2000
3000
发芽种子粒数
80
239
403
559
802
1594
2403
发芽频率
根据以上数据,该郁金香种子发芽的概率约为( )
A、 B、 C、 D、6. 如图,是一个“机器图”,它直观地表示了自变量和因变量之间的关系,即“输入”一个x的值,就可以“输出”一个y的值.下列说法不正确的是( ) A、当时, B、当自变量x的值增加1时,y的值也增加1 C、当时, D、随着自变量x的值的增大,y的值也增大7. 若的展开式中不含项和x项,则m,n的值应该是( )A、 B、 C、 D、8. 如图,在中, , 是的角平分线.若 , 则点D到的距离是( )
A、当时, B、当自变量x的值增加1时,y的值也增加1 C、当时, D、随着自变量x的值的增大,y的值也增大7. 若的展开式中不含项和x项,则m,n的值应该是( )A、 B、 C、 D、8. 如图,在中, , 是的角平分线.若 , 则点D到的距离是( ) A、2 B、4 C、3 D、6
A、2 B、4 C、3 D、6二、填空题
-
9. 计算:=10. 如图,在等腰三角形中, , 则y与x的关系式是(不需要写出x的取值范围)
 11. 牛顿在《自然哲学的数学原理》一书中系统地介绍了万有引力定律,即宇宙间任何两个质点都存在相互吸引力,其大小与两质点的质量 , 乘积成正比,与它们之间距离r的平方成反比,用数学公式表示为 , 其中 , 为万有引力常数,将数据0.0000000000667用科学记数法可表示为 .12. 若 , 则 .13. 如图,是等腰三角形, , 且B,C,D三点共线.连接 , 分别交于点M,N,连接 , 则= .
11. 牛顿在《自然哲学的数学原理》一书中系统地介绍了万有引力定律,即宇宙间任何两个质点都存在相互吸引力,其大小与两质点的质量 , 乘积成正比,与它们之间距离r的平方成反比,用数学公式表示为 , 其中 , 为万有引力常数,将数据0.0000000000667用科学记数法可表示为 .12. 若 , 则 .13. 如图,是等腰三角形, , 且B,C,D三点共线.连接 , 分别交于点M,N,连接 , 则= .
三、解答题
-
14. .15. 如图所示的是某飞机机翼设计图的一部分,请以直线l为对称轴补全机翼.
 16. 先化简,再求值: , 其中 , .17. 如图,已知 , 请用尺规作图法在BC边上找一点P,使得 . (不写作法,保留作图痕迹)
16. 先化简,再求值: , 其中 , .17. 如图,已知 , 请用尺规作图法在BC边上找一点P,使得 . (不写作法,保留作图痕迹)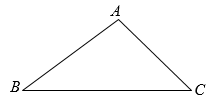 18. 如图, , 且 , , 试说明 .
18. 如图, , 且 , , 试说明 . 19. 将四个长与宽分别为a,b的相同的小长方形拼成如图所示的图形,请你认真观察图形,写出你发现的等式(用含a,b的代数式表示),并说明理由.
19. 将四个长与宽分别为a,b的相同的小长方形拼成如图所示的图形,请你认真观察图形,写出你发现的等式(用含a,b的代数式表示),并说明理由. 20. 一个不透明的口袋中装有4个红球,6个白球,8个黄球,这些球除颜色外其他均相同,从中任意摸出一个球.(1)、求摸到的球是白球的概率.(2)、要使摸到黄球的概率为 , 需要在这个口袋中再放入多少个黄球?21. 完成推理并填空:如图,点B,E分别在上, , 试说明 .
20. 一个不透明的口袋中装有4个红球,6个白球,8个黄球,这些球除颜色外其他均相同,从中任意摸出一个球.(1)、求摸到的球是白球的概率.(2)、要使摸到黄球的概率为 , 需要在这个口袋中再放入多少个黄球?21. 完成推理并填空:如图,点B,E分别在上, , 试说明 .
解:因为(已知),(对顶角相等),
所以(等量代换),
所以 ▲ ▲ ( )
所以( )
又因为(已知),
所以 ▲ = ▲ (等量代换),
所以 ▲ ▲ (内错角相等,两直线平行),
所以( )
22. 小明和小宇想用刚学过的数学知识来测量科艺楼的高,他们设计的测量方案是小明站在科艺楼与旗杆之间的空地上点P处,不断尝试调整位置,使得站在点P处看向旗杆顶部点M时,视线与水平线的夹角 , 小明转身面向科艺楼,看向科艺楼顶部点A时的视线与水平线的夹角 , 此时,小宇测量发现点P到科艺楼的距离和旗杆的部分的高度都是6米,测量旗杆与楼之间的距离米,小明眼睛到地面是米,请你计算科艺楼的高. 23. 体育课上,老师对男生的1000米长跑进行了测试,如图所示的是小玮和小哲同学的路程s(米)与时间t(分钟)之间关系的图象,根据图象解答下列问题:
23. 体育课上,老师对男生的1000米长跑进行了测试,如图所示的是小玮和小哲同学的路程s(米)与时间t(分钟)之间关系的图象,根据图象解答下列问题: (1)、2分钟时,两人谁跑在前面?(2)、两人谁先跑到终点?(3)、起跑后两人第一次相遇时距离终点多少米?24. 如图 , 点C在上, , 平分 , 且平分 .
(1)、2分钟时,两人谁跑在前面?(2)、两人谁先跑到终点?(3)、起跑后两人第一次相遇时距离终点多少米?24. 如图 , 点C在上, , 平分 , 且平分 . (1)、试猜想的位置关系,并说明理由.(2)、试猜想∠1与∠B的数量关系,并说明理由.
(1)、试猜想的位置关系,并说明理由.(2)、试猜想∠1与∠B的数量关系,并说明理由.
