陕西省西安市临潼区2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列式子中，属于最简二次根式的是（）

A、 $\sqrt{1.5}$ B、 $\sqrt{15}$ C、 $\sqrt{\frac{3}{2}}$ D、 $\sqrt{8}$

查看试题解析
2. 在以下列数值为边长的三角形中，不是直角三角形的是（）

A、 $5$ ， $12$ ， $13$ B、 $6$ ， $8$ ， $10$ C、 $7$ ， $23$ ， $25$ D、 $8$ ， $15$ ， $17$

查看试题解析
3. 已知关于x的一元二次方程（a﹣2）x²﹣2x+a²﹣4=0有一个根为0，则a的值为（）

A、0 B、±2 C、2 D、﹣2

查看试题解析
4. 一次函数y=﹣3x+2的图象不经过（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 在九年级体育中考中，某班参加排球测试的一组女生（每组 $8$ 人）测试成绩如下（单位：次 $/$ 分）： $46$ ， $44$ ， $43$ ， $42$ ， $50$ ， $46$ ， $47$ ， $45$ ．则这组数据的中位数是（）

A、 $45$ B、 $46$ C、 $45.5$ D、 $47$

查看试题解析
6. 下列说法正确的是（）

A、一组对边平行另一组对边相等的四边形是平行四边形 B、对角线互相垂直平分的四边形是菱形 C、对角线相等的四边形是矩形 D、对角线互相垂直且相等的四边形是正方形

查看试题解析
7. 已知点 $(x_{1} ， - 5) (x_{2} ， 2)$ 都在直线 $y = - 2 x + b$ 上，则 $x_{1}$ 与 $x_{2}$ 的大小关系为（）

A、 $x_{1} > x_{2}$ B、 $x_{1} = x_{2}$ C、 $x_{1} < x_{2}$ D、无法比较

查看试题解析
8. 如图，矩形ABCD的对角线AC，BD相交于点O，过点O作 $O E ⊥ A C$ 交AD于E，若 $A B = 4 ， B C = 8$ ，则AE的长为（）

A、3 B、4 C、5 D、 $2 \sqrt{10}$

查看试题解析

二、填空题

9. 若二次根式 $\sqrt{1 - 2 x}$ 有意义，则x的取值范围是．

查看试题解析
10. 跳高训练时，甲、乙两名同学在相同条件下各跳了10次，统计他们的平均成绩都是1.36米，且方差为 $s^{2}_{甲} =0 .4$ ， $s^{2}_{乙} = 0.3$ ，则成绩较为稳定的是（填“甲”或“乙”）．

查看试题解析
11. 直线 $y = - \frac{1}{2} x - 1$ 向上平移 $m$ 个单位长度，得到直线 $y = - \frac{1}{2} x + 4$ ，则 $m =$ ．

查看试题解析
12. 如图，桌上有一个圆柱形玻璃杯（无盖），高 $6$ 厘米，底面周长 $16$ 厘米，在杯口内壁离杯口 $1.5$ 厘米的 $A$ 处有一滴蜜糖，在玻璃杯的内壁， $A$ 的相对方向有一小虫 $P$ ，小虫离杯底的垂直距离为 $1.5$ 厘米，小虫爬到蜜糖处的最短距离是厘米．

查看试题解析
13. 如图，在矩形 $A B C D$ 中， $A B = 4$ ， $A D = 6$ ，点 $P$ 在边 $A D$ 上，点 $Q$ 在边 $B C$ 上，且 $A P = C Q$ ，连接 $C P$ ， $Q D$ ，则 $P C + Q D$ 的最小值等于．

查看试题解析

三、解答题

14. 计算： $(\sqrt{2} - 1) (\sqrt{2} + 1) + \sqrt{12} - (- 1)^{0}$ ．

查看试题解析
15. 解方程：

(1)、 $x^{2} - 6 x + 5 = 0$ ；

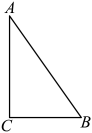
(2)、 $2 x^{2} - x + 1 = 4$ ．

查看试题解析
16. 《九章算术》中有一道“折竹”问题：“今有竹高一丈，末折抵地，去根三尺，问折者高几何？”题意是：有一根竹子原高1丈（1丈=10尺），中部有一处折断，竹梢触地面处离竹根3尺，试问折断处离地面多高？

查看试题解析
17. 已知：如图，点E，F分别为 $▱ A B C D$ 的边BC，AD上的点，且 $∠ 1 = ∠ 2$ .求证： $A F = C E$ .

查看试题解析
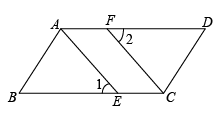18. 如图，从一个大正方形中裁去面积为 $12 c m^{2}$ 和 $15 c m^{2}$ 的两个小正方形，求留下部分的面积．

查看试题解析
19. 已知函数 $y = 2 x - 4$ ．

(1)、填表，并画出这个函数的图象；
$x$
$\dots$
$0$
▲
$\dots$
$y = 2 x - 4$
$\dots$
▲
$0$
$\dots$

(2)、判断点 $A (3 ， 1)$ 是否在该函数的图象上，并说明理由．

查看试题解析
20. 某公司对应聘者进行面试，按专业知识、工作经验、仪表形象给应聘者打分，这三个方面的重要性之比为 $5 ： 4 ： 1$ ，应聘的甲、乙两人的打分如下表：

甲
乙
专业知识
$16$
$18$
工作经验
$17$
$16$
仪表形象
$18$
$14$
如果两人中只录取一人，若你是人事主管，你会录用谁？

查看试题解析
21. 已知一次函数的图象与 $y = - x$ 的图象平行，且经过点 $(2 ， 3)$ ，求此一次函数图象与 $x$ 轴的交点坐标．

查看试题解析
22. 为积极响应“弘扬传统文化”的号召，某学校倡导全校开展了以“畅游书海，阅动心智”为主题的读书活动 $.$ 学校政教处对本校七年级学生四月份“阅读该主题相关书籍的读书量” $($ 下面简称“读书量” $)$ 进行了随机抽样调查，并对所有随机抽取的学生的“读书量”进行了统计，如图：

根据以上信息解答下列问题：

(1)、补全条形统计图，本次所抽取的学生四月份“读书量”的众数为；

(2)、求本次所抽取的学生四月“读书量”的平均数；

(3)、已知该校七年级有 $1400$ 名学生，请你估计该校七年级学生中，四月份“读书量”为 $5$ 本的学生人数．

查看试题解析
23. 为落实“精准扶贫”精神，市农科院专家指导贫困户李大爷种植优质百香果喜获丰收，上市20天全部销售完，专家对销售情况进行了跟踪记录，并将记录情况绘成图象，日销售量y(单位：千克)与上市时间x(单位：天)的函数关系如图所示.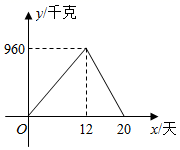

(1)、观察图示，直接写出日销售量的最大值为；

(2)、根据图示，求李大爷家百香果的日销售量y与上市时间x的函数解析式，并求出第15天的日销售量.

查看试题解析
24. 如图，△ABC中，AB=AC，AD是△ABC的角平分线，点O为AB的中点，连接DO并延长到点E，使OE=OD，连接AE，BE．

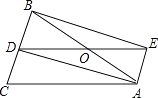(1)、求证：四边形AEBD是矩形；

(2)、当△ABC满足什么条件时，矩形AEBD是正方形，并说明理由

查看试题解析
25. 张先生准备在一家房屋中介租房开公司．该中介有甲、乙两类房屋出租，甲类房屋精装修，乙类房屋是毛坯房，同一类房屋的月租相同．若两类房屋各租一间月租共5000元；甲类房租2间，乙类房租3间，月租共12000元．

(1)、甲、乙两类房屋每间月租多少元？

(2)、张先生打算租一间房，可以租甲类房，也可以租乙类房，但是租乙类房必须按甲类房的规格装修，需要装修费20000元，请你自行定义变量，建立函数，利用函数有关的知识帮助张先生设计一个租房方案（只从最省钱的角度设计租房方案）．

查看试题解析
26. 如图，直线 $y = k x + 6 (k \neq 0)$ 与 $x$ 轴， $y$ 轴分别交于点 $E$ ， $F$ ，点 $E$ 的坐标为 $(- 8 ， 0)$ ，点 $A$ 的坐标为 $(- 6 ， 0)$ ，点 $P (x ， y)$ 是线段 $E F$ 上的一个动点．

(1)、求 $k$ 的值；

(2)、求点 $P$ 在运动过程中 $△ O P A$ 的面积 $S$ 与 $x$ 的函数关系式，并写出自变量 $x$ 的取值范围；

(3)、求 $△ O P A$ 面积的最大值．

查看试题解析

	甲	乙
专业知识	$16$	$18$
工作经验	$17$	$16$
仪表形象	$18$	$14$

$x$	$\dots$	$0$	▲	$\dots$
$y = 2 x - 4$	$\dots$	▲	$0$	$\dots$