陕西省西安市临潼区2022-2023学年七年级下学期期末数学试题

试卷更新日期：2023-08-24 类型：期末考试

进入出卷网下载

一、单选题

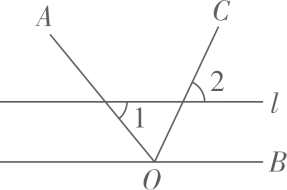
1. 16的算术平方根是（）

A、4 B、－4 C、±4 D、 $\sqrt{4}$

查看试题解析
2. 如图，OC是∠AOB的角平分线，l//OB，若∠1=52°，则∠2的度数为（）

A、52° B、54° C、64° D、69°

查看试题解析
3. 已知 $a < b$ 则下列各式中一定成立的是（）

A、 $a - b > 0$ B、 $- 2 a > - 2 b$ C、 $a c^{2} < b c^{2}$ D、 $\frac{a}{3} > \frac{b}{3}$

查看试题解析
4. 以下问题不适合用抽样调查的时（）

A、学校对应聘教师的面试 B、了解某地区居民的防火意识 C、调查市场上某食品色素含量 D、检测某城市空气质量

查看试题解析
5. 解为 ${\begin{matrix} x = 1 \\ y = 2 \end{matrix}$ 的方程组是（）

A、 ${\begin{matrix} x - y = 1 \\ 3 x + y = 5 \end{matrix}$ B、 ${\begin{matrix} x - y = - 1 \\ 3 x + y = - 5 \end{matrix}$ C、 ${\begin{matrix} x - y = 3 \\ 3 x - y = 1 \end{matrix}$ D、 ${\begin{matrix} x - 2 y = - 3 \\ 3 x + y = 5 \end{matrix}$

查看试题解析
6. 已知 $a < b < 0$ ，则点 $A (a - b ， b)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 为保住耕地红线，宁夏某县响应国家号召，将一部分林地改为耕地，改变后，耕地面积和林地面积共有180平方千米，林地面积是耕地面积的 $25 %$ ，求改变后林地面积和耕地面积各多少平方千米？设改变后耕地面积x平方千米，林地面积y平方千米，根据题意，下面的方程组中正确的是（）

A、 ${\begin{array}{l} x + y = 180 \\ y = x \cdot 25 % \end{array}$ B、 ${\begin{array}{l} x + y = 180 \\ x = y \cdot 25 % \end{array}$ C、 ${\begin{array}{l} x + y = 180 \\ x - y = 25 % \end{array}$ D、 ${\begin{array}{l} x + y = 180 \\ y - x = 25 % \end{array}$

查看试题解析
8. 不等式组 ${\begin{matrix} 5 x - 3 < 3 x + 5 \\ x < a \end{matrix}$ 的解集为x＜4，则a满足的条件是（）

A、a＜4 B、a=4 C、a≤4 D、a≥4

查看试题解析

二、填空题

9. 已知 $a$ 、 $b$ 为两个连续的整数，且 $a < \sqrt{5} < b$ ，则 $a^{b} =$ ．

查看试题解析
10. 不等式 $4 x \leq 12$ 的正整数解的和为．

查看试题解析
11. 如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法，其理由是．

查看试题解析
12. 已知点 $E (b + 1 ， 2)$ 和点 $F (3 ， - 5)$ ，若 $E F ∥ y$ 轴，则 $b =$ ．

查看试题解析
13. 若关于x，y的方程组 ${\begin{array}{l} 2 x + y = 4 \\ x + 2 y = - 3 m + 2 \end{array}$ 的解满足 $x - y > - \frac{3}{2}$ ，则 $m$ 的最小整数解为．

查看试题解析

三、解答题

14. 计算： $| - 3 | + \sqrt{2} \times (\sqrt{2} - 1) - \sqrt[3]{8}$ ．

查看试题解析
15. 解方程组 ${\begin{array}{l} x + 2 y = 1 \\ 3 x - 4 y = 5 \end{array}$ ．

查看试题解析
16. 解不等式组 ${\begin{array}{l} x + 1 \geq 0 \\ \frac{2 x - 1}{3} < x - 1 \end{array}$ ，并把解集在数轴上表示出来．

查看试题解析
17. 如图，已知点 $A (- 4 ， 1)$ ， $B (- 2 ， 3)$ ， $C (- 1 ， 0)$ ， $△ A B C$ 经过平移得到的 $△ A^{'} B^{'} C^{'}$ ， $△ A B C$ 中任意一点 $P (x_{1} ， y_{1})$ 平移后的对应点为 $P^{'} (x_{1} + 5 ， y_{1} - 1)$

(1)、请在图中作出 $△ A^{'} B^{'} C^{'}$

(2)、写出点 $A^{'}$ 、 $B^{'}$ 、 $C^{'}$ 的坐标．

查看试题解析
18. 某种商品的进价为80元，出售时标价为120元，后来由于该商品积压，商店准备打折出售，但要保证利润率不低于5%，则至多可打几折？

查看试题解析
19. 已知关于x，y的方程组 ${\begin{array}{l} 2 x - 3 y = 1 \\ a x + b y = 2 \end{array}$ 的解和 ${\begin{array}{l} 2 a x - b y = - 1 \\ x + y = 3 \end{array}$ 的解相同，求代数式 $\frac{a}{b}$ 的值．

查看试题解析
20. 把一些书作为参加运动会获奖学生的奖品，如果每人分3本，那么余8本；如果前面的每名同学分5本，那么最后一人就不足3本，但不少于1本．求共有多少名学生获奖？

查看试题解析
21. 如图，已知 $A D ∥ E C$ ， $∠ 1 = ∠ B D C$ ，求证： $∠ 2 + ∠ 3 = 180 °$ ．

查看试题解析
22.
如图，8块相同的长方形地砖拼成一个长方形，每块长方形地砖的长和宽分别是多少？

查看试题解析

23. 某市为了解学生垃圾分类知识掌握情况，组织全市学生参加垃圾分类知识竞赛，随机抽取了部分参赛学生的成绩，整理并制作出如下不完整的统计表和统计图，如图所示，请根据图表信息解答以下问题．

组别	成绩x/分	频数
A组	$60 \leq x < 70$	a
B组	$70 \leq x < 80$	8
C组	$80 \leq x < 90$	12
D组	$90 \leq x < 100$	14

(1)、表中

a =

，并补全频数分布直方图．

(2)、计算扇形统计图中“B”对应的圆心角度数；

(3)、若成绩在80分以上（包括80分）的为“优”等，该市共有学生120万人，那么该市学生中能获得“优秀”的有多少人？

查看试题解析

24. 已知二元一次方程 $2 x - y = 2$ ．

(1)、请任意写出此方程的三组解；

(2)、若 ${\begin{array}{l} x = x_{0} \\ y = y_{0} \end{array}$ 为此方程的一组解，我们规定 $(x_{0} ， y_{0})$ 为某一点的坐标，请根据你在（1）中写出的三组解，对应写出三个点的坐标，并将这三个点描在平面直角坐标系中；

(3)、观察这三个点的位置，你发现了什么？

查看试题解析
25. 为实现区域教育均衡发展，我市计划对某县A、B两类薄弱学校全部进行改造，根据预算，共需资金1575万元，改造一所A类学校和两所B类学校共需资金230万元；改造两所A类学校和一所B类学校共需资金205万元．

(1)、改造一所A类学校和一所B类学校所需的资金分别是多少万元；

(2)、我市计划今年对该县A、B两类学校共6所进行改造，改造资金由国家财政和地方财政共同承担．若今年国家财政拨付的改造资金不超过400万元；地方财政投入的改造资金不少于70万元，其中地方财政投入到A、B两类学校的改造资金分别为每所10万元和15万元．请你通过计算求出有几种改造方案．

查看试题解析
26. 阅读下列材料：
小明同学遇到下列问题：解方程组 ${\begin{array}{l} \frac{2 x + 3 y}{4} + \frac{2 x - 3 y}{3} = 7 \\ \frac{2 x + 3 y}{3} + \frac{2 x - 3 y}{2} = 8 \end{array}$ 小明发现如果用代入消元法或加减消元法求解，运算量比较大，容易出错．如果把方程组中的（2x+3y）看成一个整体，把（2x﹣3y）看成一个整体，通过换元，可以解决问题．以下是他的解题过程：令m＝2x+3y，n＝2x﹣3y．原方程组化为 ${\begin{array}{l} \frac{m}{4} + \frac{n}{3} = 7 \\ \frac{m}{3} + \frac{n}{2} = 8 \end{array}$ ，解的 ${\begin{array}{l} m = 60 \\ n = - 24 \end{array}$ ，把 ${\begin{array}{l} m = 60 \\ n = - 24 \end{array}$ 代入m＝2x+3y，n＝2x﹣3y，得 ${\begin{array}{l} 2 x + 3 y = 60 \\ 2 x - 3 y = - 24 \end{array}$ 解得 ${\begin{array}{l} x = 9 \\ y = 14 \end{array}$ 所以，原方程组的解为 ${\begin{array}{l} x = 9 \\ y = 14 \end{array}$ ．
请你参考小明同学的做法解方程组：

(1)、 ${\begin{array}{l} \frac{x + y}{6} + \frac{x - y}{10} = 3 \\ \frac{x + y}{6} - \frac{x - y}{10} = - 1 \end{array}$ ；

(2)、 ${\begin{array}{l} \frac{5}{x} + \frac{2}{y} = 11 \\ \frac{3}{x} - \frac{2}{y} = 13 \end{array}$ ．

查看试题解析