陕西省西安市西咸新区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-24 类型:期末考试
一、单选题
-
1. 下列各图中不是中心对称图形的是( )A、
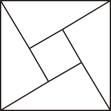 B、
B、 C、
C、 D、
D、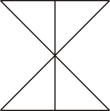 2. 若 , 则下列关系不正确的是( )A、 B、 C、 D、3. 如图,是等边三角形,D,E别是的中点,连接 , 若 , 则的周长为( )
2. 若 , 则下列关系不正确的是( )A、 B、 C、 D、3. 如图,是等边三角形,D,E别是的中点,连接 , 若 , 则的周长为( )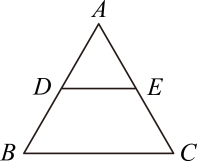 A、15 B、20 C、25 D、304. 下列等式从左到右的变形,属于因式分解的是( )A、 B、 C、 D、5. 一次函数与的图像如下图所示,则的解集为( )
A、15 B、20 C、25 D、304. 下列等式从左到右的变形,属于因式分解的是( )A、 B、 C、 D、5. 一次函数与的图像如下图所示,则的解集为( )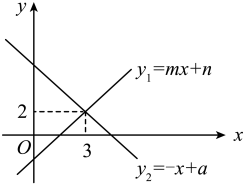 A、 B、 C、 D、6. 在四边形中, , 若四边形是平行四边形,则还需要满足( )A、 B、 C、 D、7. 已知 , , 则的值为( )A、-2 B、1 C、-1 D、28. 如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F,连接AC、CF. 下列结论:①△ABC≌△EAD;②△ABE是等边三角形;③AD=AF;④S△BEF=S△ABE . 其中正确的有( )
A、 B、 C、 D、6. 在四边形中, , 若四边形是平行四边形,则还需要满足( )A、 B、 C、 D、7. 已知 , , 则的值为( )A、-2 B、1 C、-1 D、28. 如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F,连接AC、CF. 下列结论:①△ABC≌△EAD;②△ABE是等边三角形;③AD=AF;④S△BEF=S△ABE . 其中正确的有( )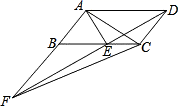 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 要使分式有意义,则的取值范围为 .10. 正十五边形其中一个内角的度数为 .11. 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=10,将△ABC沿CB方向向右平移得到△DEF . 若四边形ABED的面积为20,则平移距离为 .
 12. 若关于的方程有增根,则的值是 .13. 如图在中, , D是上一点,且 , F是延长线上一点, , , 连接交于E,若 , 则线段的长为 .
12. 若关于的方程有增根,则的值是 .13. 如图在中, , D是上一点,且 , F是延长线上一点, , , 连接交于E,若 , 则线段的长为 .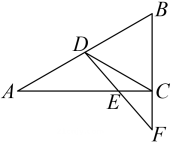
三、解答题
-
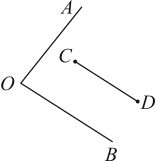
14. 分解因式: .15. 解方程: .16. 如图,已知和线段 , 请用尺规作图法在线段上找一点P,使得点P到的距离相等.(保留作图痕迹,不写作法)
 17. 解不等式组: , 并把解集在数轴上表示出来.
17. 解不等式组: , 并把解集在数轴上表示出来.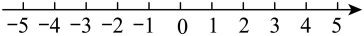 18. 某车间工人刘伟接到一项任务,要求10天内加工完190个零件,最初2天,每天加工15个,要在规定时间内完成任务,以后平均每天至少加工多少个零件?19. 如图,已知在中,D、E是上两点,且 , 求证: .
18. 某车间工人刘伟接到一项任务,要求10天内加工完190个零件,最初2天,每天加工15个,要在规定时间内完成任务,以后平均每天至少加工多少个零件?19. 如图,已知在中,D、E是上两点,且 , 求证: .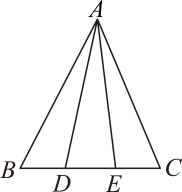 20. 已知:如图,在中,D、E分别是的中点,连接 , 过点E作交的延长线于点F.求证: .
20. 已知:如图,在中,D、E分别是的中点,连接 , 过点E作交的延长线于点F.求证: .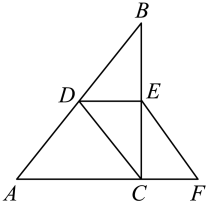 21. 先化简,再求值: , 其中 .22. 如图,在平面直角坐标系中,已知点 , , , 请解答下列问题:
21. 先化简,再求值: , 其中 .22. 如图,在平面直角坐标系中,已知点 , , , 请解答下列问题: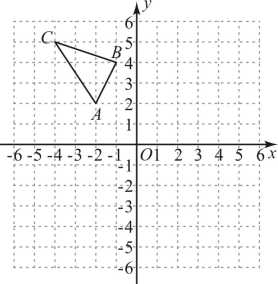
⑴若经过平移后得到 , 已知点的坐标为作出并写出其余两个顶点的坐标;
⑵将绕点O按顺时针方向旋转得到 , 作出 .
23. 某药品生产车间引进智能机器人替换人工包装药品,每台机器人每小时包装的速度是人工包装速度的5倍,经过测试,由1台智能机器人包装1600盒药品的时间,比4个工人包装同样数量的药品节省4小时.一台智能机器人每小时可以包装多少盒药品?24. 阅读材料,并解决问题:分解因式 .
解:设 , 则原式 .
这样的解题方法叫做“换元法”,即当复杂的多项式中某一部分重复出现时,我们用字母将其替换,从而简化这个多项式.换元法是一个重要的数学方法,不少问题能用换元法解决.
请你用“换元法”对下列多项式进行因式分解:
(1)、;(2)、 .25. 如图,在平行四边形中,对角线、交于点O, , , 垂足分别为E、F.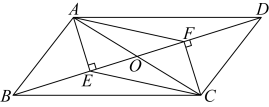 (1)、求证:四边形是平行四边形;(2)、若 , , 求四边形的面积.26. 解决问题
(1)、求证:四边形是平行四边形;(2)、若 , , 求四边形的面积.26. 解决问题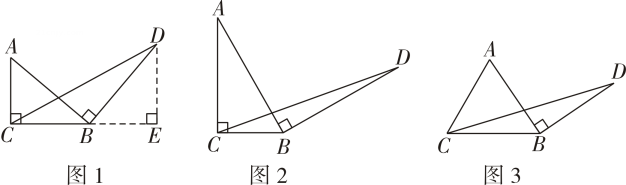 (1)、感知:
(1)、感知:如图1,在等腰三角形ABC中,∠ACB=90°,BC=x,将边AB绕点B顺时针旋转90°得到线段BD,过点D作DE⊥CB交CB的延长线于点E,连接CD.则线段BC与DE的数量关系是 , △BCD的面积为(用含x的式子表示);
(2)、应用:如图2,在一般的Rt△ABC中,∠ACB=90°,BC=x,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,用含x的式子表示△BCD的面积,并说明理由.
(3)、拓展:如图3所示,在等腰三角形ABC中,AB=AC=5,将边AB绕点B顺时针旋转,当AB⊥BD,连接CD,若△BCD的面积为9,则CD的长为.