江苏省连云港市灌南县2022-2023学年八年级下册数学期末试卷

试卷更新日期：2023-08-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 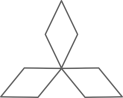B、 C、 D、

查看试题解析
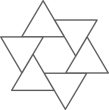2. 下列适合抽样调查的是（）

A、了解某一药品的有效性 B、了解本班学生的视力情况 C、某单位组织职工到医院检查身体 D、对组成人造卫星零部件的检查

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{18} \div \sqrt{2} = 3$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $\sqrt{3} \times 3 \sqrt{3} = 6$ D、 $\sqrt{18} - \sqrt{12} = \sqrt{6}$

查看试题解析
4. 从一副扑克牌中任意抽取1张，则下列事件中发生的可能性最大的是（）

A、这张牌是“ $A$ ” B、这张牌是“红心” C、这张牌是“大王” D、这张牌是“红色的”

查看试题解析
5. 计算 ${(\sqrt{3})}^{2}$ 的结果是（）

A、 $\sqrt{3}$ B、3 C、 $2 \sqrt{3}$ D、9

查看试题解析
6. 数学家斐波那契编写的《算经》中有如下问题：一组人平分100元钱，每人分得若干，若再加上5人，平分150元钱，则第二次每人所得与第一次相同，求第二次分钱的人数．设第二次分钱的人数为x人，则可列方程为（）

A、 $100 x = 150 (x + 5)$ B、 $100 (x - 5) = 150 x$ C、 $\frac{100}{x} = \frac{150}{x + 5}$ D、 $\frac{100}{x - 5} = \frac{150}{x}$

查看试题解析
7. 若关于x的方程 $\frac{m x - 1}{x - 1} = 3$ 无解，则m的值为（）

A、1 B、1或3 C、1或2 D、2或3

查看试题解析
8. 如图，矩形OABC与反比例函数 $y_{1} = \frac{k_{1}}{x}$ （k₁是非零常数，x>0）的图象交于点M，N，与反比例函数 $y_{2} = \frac{k_{2}}{x}$ （k₂是非零常数，x>0）的图象交于点B，连接OM，ON．若四边形OMBN的面积为3，则k₁-k₂=（）

A、3 B、-3 C、 $\frac{3}{2}$ D、 $- \frac{3}{2}$

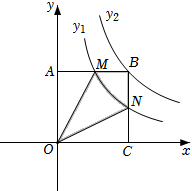查看试题解析

二、填空题

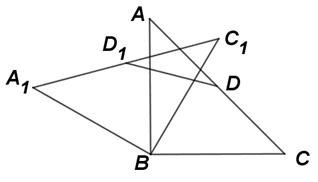
9. 若分式 $\frac{x - 2}{x + 5}$ 的值为0，则x的值是．

查看试题解析
10. 分式 $\frac{1}{x}$ ， $\frac{1}{2 x}$ 与 $\frac{1}{3 x^{2}}$ 的最简公分母是．

查看试题解析
11. 最简二次根式 $\sqrt{x - 1}$ 与 $\sqrt{18}$ 是同类二次根式，则 $x$ 的值是．

查看试题解析
12. 若 $\sqrt{3} < m < \sqrt{7}$ ，其中 $m$ 是正整数，则 $m$ 的值是．

查看试题解析
13. 若反比例函数y＝ $\frac{m - 2}{x}$ 的图像经过第二、四象限，则m的取值范围是．

查看试题解析
14. 如图，在 $△ A B C$ 中， $∠ A B C = 90 °$ ， $A B = B C = 2$ .将 $△ A B C$ 绕点B逆时针旋转60°，得到 $△ A_{1} B C_{1}$ ，则 $A C$ 边的中点D与其对应点 $D_{1}$ 的距离是.

查看试题解析
15. 关于x的方程 $\frac{2 x + a}{x - 1} = 1$ 的解是正数，则a的取值范围是．

查看试题解析
16. 在正方形 $A B C D$ 中， $E$ 是 $B C$ 的中点， $F$ 、 $G$ 分别是边 $A B$ 、 $C D$ 上的动点，且 $F G ⊥ A E$ 交 $A E$ 于 $M$ ，连接 $E F$ 和 $A G$ ，当 $A B = 2$ 时，则 $E F + A G$ 的最小值为．

查看试题解析

三、解答题

17. 计算：

(1)、 $(\sqrt{24} - \sqrt{\frac{2}{3}}) \div \sqrt{6}$ ；

(2)、 $(\sqrt{5} + 1) (\sqrt{5} - 1) - {(\sqrt{3} - \sqrt{2})}^{2}$ ．

查看试题解析
18. 解分式方程：

(1)、 $\frac{9}{x} = \frac{8}{x - 1}$ ；

(2)、 $\frac{1}{x - 2} - 3 = \frac{x - 1}{2 - x}$ ．

查看试题解析
19. 先化简再求值： $1 - \frac{x - 2}{x} \div \frac{x^{2} - 4}{x^{2} + x}$ ，其中 $x = \sqrt{3} - 2$ .

查看试题解析
20. 近年来，随着人们健康睡眠的意识不断提高，社会各界对于初中生的睡眠时间是否充足越发关注．近日我市某学校从全校1200人中随机抽取了部分同学，调查他们平均每日睡眠时间，将得到的数据整理后绘制了如图所示的扇形统计图和频数分布直方图：

(1)、本次接受调查人数为；图中a=；b=；c=.

(2)、教育部《关于进一步加强中小学生睡眠管理工作的通知》文件指出，初中生睡眠时间应达到9小时，试估算该校学生睡眠时间达标人数．

查看试题解析
21. 在 $▱ A B C D$ 中，

(1)、若 $∠ A = 45 °$ ，如图1，点 $E$ 、 $F$ 分别是边 $A D$ 、 $A B$ 的中点， $A D = 3 \sqrt{2}$ ， $A B = 7$ ，求 $E F$ 的长；

(2)、若 $∠ A = 90 °$ ，如图2，点 $E$ 、 $F$ 分别是边 $A D$ 、 $A B$ 的中点，请仅用无刻度的直尺在图2中画一个以 $E F$ 为边的菱形 $E F G H$ ．（不写作法，保留作图痕迹，标明字母）

查看试题解析
22. “元旦节”前夕，某商场根据市场调查，用3000元购进第一批盒装饼干，上市后很快售完，接着又用7500元购进第二批这种盒装瓶干．已知第二批所购瓶干的盒数是第一批所购瓶干盒数的3倍，且每盒的进价比第一批的进价少4元，求第一批盒装瓶干每盒的进价是多少元？

查看试题解析
23. 某水果生产基地在气温较低时，用装有恒温系统的大棚栽培一种新品种水果，如图是试验阶段的某天恒温系统从开启到关闭后，大棚内的温度 $y (℃)$ 与时间 $x (h)$ 之间的函数关系，其中线段 $A B$ 、 $B C$ 表示恒温系统开启后阶段，双曲线的一部分 $C D$ 表示恒温系统关闭阶段．
请根据图中信息解答下列问题：

(1)、这个恒温系统设定的恒定温度为多少 $℃$ ；

(2)、求全天的温度 $y (℃)$ 与时间 $x (h)$ 之间的函数表达式；

(3)、若大棚内的温度低于 $10 ℃$ 时，蔬菜会受到伤害．问：这天内恒温系统最多可以关闭多少小时，才能避免水果生长受到影响？

查看试题解析
24. 先阅读材料，然后回答问题：
形如 $\sqrt{a \pm 2 \sqrt{b}}$ 的化简，只要找到两个正数 $x$ 、 $y$ ，使 $x + y = a$ ， $x y = b$ ，

使得 ${(\sqrt{x})}^{2} + {(\sqrt{y})}^{2} = a$ ， $\sqrt{x} \cdot \sqrt{y} = b$ ，

那么则有 $\sqrt{a \pm 2 \sqrt{b}} = \sqrt{{(\sqrt{x} \pm \sqrt{y})}^{2}} = \sqrt{x} \pm \sqrt{y} (x > y)$ ，例如：化简 $\sqrt{6 - 2 \sqrt{5}}$ ， $\sqrt{6 - 2 \sqrt{5}} = \sqrt{5 - 2 \sqrt{5 \times 1} + 1} = \sqrt{{(\sqrt{5})}^{2} - 2 \sqrt{5} \times \sqrt{1} + {(\sqrt{1})}^{2}} = \sqrt{{(\sqrt{5} - \sqrt{1})}^{2}} = \sqrt{5} - 1$ ．

(1)、请根据你从上述材料中得到的启发，化简： $\sqrt{5 - 2 \sqrt{6}} =$ ； $\sqrt{7 + 4 \sqrt{3}} =$ ；

(2)、在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 15 °$ ，其中 $A B$ 边的垂直平分线分别交 $A B$ 、 $B C$ 于点 $D$ 、 $E$ ，当 $A C = 1$ 时，求 $A B$ 的长．（结果要化为最简形式）

查看试题解析
25. 如图，一次函数y=mx+1的图象与反比例函数y= $\frac{k}{x}$ 的图象相交于A、B两点，点C在x轴正半轴上，点D(1，-2)，连接OA、OD、DC、AC ，四边形OACD为菱形．

(1)、求一次函数与反比例函数的解析式；

(2)、根据图象，直接写出反比例函数的值小于2时，x的取值范围；

(3)、设点P是直线AB上一动点，且S_△OAP= $\frac{1}{2}$ S_菱形OACD ，求点P的坐标．

查看试题解析
26. 定义：若四边形有一组对角互补，一组邻边相等，且相等邻边的夹角为直角，像这样的图形称为“角等邻对补”四边形，简称“直等补”四边形．根据以上定义，解决下列问题：

(1)、如图1，以菱形 $A B C D$ 的一边 $C D$ 为边向外作正方形 $C D E F$ ， $M$ 、 $N$ 分别是菱形和正方形的对角线交点，连接 $M N$ ．
求证：四边形 $D M C N$ 是“直等补”四边形．
②若 $M N = \sqrt{2}$ ，求四边形 $D M C N$ 的面积．

(2)、如图2，已知四边形 $A B C D$ 是“直等补”四边形，其中 $A B = B C = 5$ ， $C D > A B$ ，过点 $B$ 作 $B E ⊥ C D$ 于点 $E$ 且 $B E = 4$ ，连接 $B D$ ，若点 $P$ 是线段 $B D$ 上的动点，请你直接写出 $△ P E C$ 周长的最小值．

查看试题解析