江苏省连云港市东海县2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-08-24 类型:期末考试
一、单选题
-
1. 下列新能源汽车标志图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、3. 数轴上表示数a的点在原点左侧,表示数b的点在原点右侧,下列事件是随机事件的是( )A、 B、 C、 D、4. 下表是我市5月1日-7日最高气温的记录表:
2. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、3. 数轴上表示数a的点在原点左侧,表示数b的点在原点右侧,下列事件是随机事件的是( )A、 B、 C、 D、4. 下表是我市5月1日-7日最高气温的记录表:5月1日
5月2日
5月3日
5月4日
5月5日
5月6日
5月7日
21℃
25℃
27℃
29℃
28℃
30℃
26℃
如果要更直观反映我市一周每天的最高气温的变化趋势,你认为应该采用( )
A、折线统计图 B、条形统计图 C、频数分布直方图 D、扇形统计图5. 下列点中和 , 在同一个反比例函数图象上的是( )A、 , B、 , C、 , D、 ,6. 分式 可变形为( )A、 B、- C、 D、7. 如图1,直线 , 直线分别交直线 , 于点A,B.小嘉在图1的基础上进行尺规作图,得到如图2,并探究得到下面两个结论:①四边形ABCD是邻边不相等的平行四边形;②四边形ABCD是对角线互相垂直的平行四边形.下列判断正确的是( )
 A、①②都正确 B、①错误,②正确 C、①②都错误 D、①正确,②错误8. 如图,在△ABC中,AB=AC,若M是BC边上任意一点,将△ABM绕点A逆时针旋转得到△ACN,点M的对应点为点N,连接MN,则下列结论一定正确的是( )
A、①②都正确 B、①错误,②正确 C、①②都错误 D、①正确,②错误8. 如图,在△ABC中,AB=AC,若M是BC边上任意一点,将△ABM绕点A逆时针旋转得到△ACN,点M的对应点为点N,连接MN,则下列结论一定正确的是( )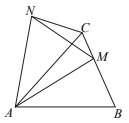 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 若分式 有意义,则x的取值范围是.10. 写出一个图象位于第二、第四象限的反比例函数的解析式 .11. 端午节期间,质监部门要对市场上粽子质量情况进行调查,适合采用的调查方式是 .(填“全面调查”或“抽样调查”)12. 投壶是中国古代一种传统礼仪和宴饮游戏.下表记录了一组游戏参与者的投查结果.

投壶次数n
50
100
150
200
250
300
400
500
投中次数m
28
46
72
104
125
153
200
250
投中频率
0.56
0.46
0.48
0.52
0.50
0.51
0.50
0.50
根据以上数据,估计这组游戏参与者投中的概率约为(结果精确到0.1).
13. 若为整数,x为正整数,则x的值为 .14. 综合实践活动课上,小亮将一张面积为6cm2 , 其中一边BC为4cm的锐角三角形纸片(如图1),经过两刀裁剪,拼成了一个无缝隙、无重叠的矩形BCDE(如图2),则矩形的周长为 . 15. 若关于x的分式方程的解为正数,则m的取值范围是 .16. 如图,矩形中, , , 点O为矩形的对称中心,点E为边上的动点,连接并延长交于点F . 将四边形沿着翻折,得到四边形边交边于点G , 连接、 , 则的面积的最小值为 .
15. 若关于x的分式方程的解为正数,则m的取值范围是 .16. 如图,矩形中, , , 点O为矩形的对称中心,点E为边上的动点,连接并延长交于点F . 将四边形沿着翻折,得到四边形边交边于点G , 连接、 , 则的面积的最小值为 .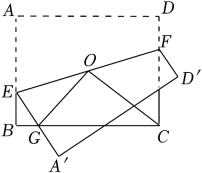
三、解答题
-
17. 计算:(1)、;(2)、 .18. 计算:(1)、;(2)、 .19. 解下列方程:(1)、;(2)、 .20. 先化简,再求值: , 其中.21. 科学课上,同学用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度h(单位:cm)是液体的密度(单位:)的反比例函数,当密度计悬浮在密度为的水中时, .
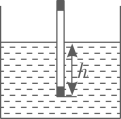 (1)、求h关于的函数解析式.(2)、当密度计悬浮在另一种液体中时, , 求该液体的密度 .22. 为了解中学生的视力情况,某区卫健部门决定随机抽取本区部分初、高中学生进行调查,并对他们的视力数据进行整理,得到如下统计表和统计图.
(1)、求h关于的函数解析式.(2)、当密度计悬浮在另一种液体中时, , 求该液体的密度 .22. 为了解中学生的视力情况,某区卫健部门决定随机抽取本区部分初、高中学生进行调查,并对他们的视力数据进行整理,得到如下统计表和统计图.整理描述
初中学生视力情况统计表
人数
百分比
8
16
28
34
m
及以上
46
n
合计
200
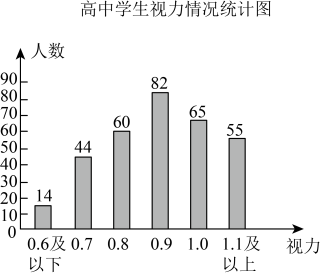
分析处理
(1)、 , ;(2)、被调查的高中学生视力情况的样本容量为 .(3)、视力未达到1.0为视力不良.若该区有26000名初中学生,估计该区有多少名初中学生视力不良?(4)、请对该区中学生视力保护提出一条合理化建议.23. 如图在平行四边形中, , 相交于点 , , 分别是 , 的中点. (1)、求证:;(2)、设 , 当k为何值时,四边形DEBF是矩形?请说明理由.24. 端午节是中国传统节日,人们有吃粽子的习俗,今年端午节来临之际,某商场进来鲜肉粽和红枣粽.每千克鲜肉粽进价比红枣粽多6元,用360元购进鲜肉粽的数量和用240元购进红枣粽的数量同样多.根据以上信息,解答下列问题:(1)、该商场每千克鲜肉粽的进价是多少元?(2)、如果该商场购进鲜肉粽和红枣粽500千克,且总费用不超过8400元,并按照鲜肉粽每千克24元,红枣粽每千克16元全部售出,那么该商场购进多少千克鲜肉粽获得利润最大?最大利润是多少?25. 【问题情境】期中调研试题中的第26题对苏科版八年级下册数学教材第94页第19题第(1)题进行了探究.小明在期末复习时,对该题进行了新的探究.
(1)、求证:;(2)、设 , 当k为何值时,四边形DEBF是矩形?请说明理由.24. 端午节是中国传统节日,人们有吃粽子的习俗,今年端午节来临之际,某商场进来鲜肉粽和红枣粽.每千克鲜肉粽进价比红枣粽多6元,用360元购进鲜肉粽的数量和用240元购进红枣粽的数量同样多.根据以上信息,解答下列问题:(1)、该商场每千克鲜肉粽的进价是多少元?(2)、如果该商场购进鲜肉粽和红枣粽500千克,且总费用不超过8400元,并按照鲜肉粽每千克24元,红枣粽每千克16元全部售出,那么该商场购进多少千克鲜肉粽获得利润最大?最大利润是多少?25. 【问题情境】期中调研试题中的第26题对苏科版八年级下册数学教材第94页第19题第(1)题进行了探究.小明在期末复习时,对该题进行了新的探究. (1)、【探究活动1】
(1)、【探究活动1】如图,在正方形中,点、、分别在边、和上,且 , 垂足为 . 那么与相等吗?证明你的结论;
(2)、【探究活动2】如图,在(1)的条件下,当M在正方形的对角线上时,连接 , 将沿着翻折,点落在点处.
①四边形是正方形吗?请说明理由;
②若 , 如图,点在上,且 , 直接写出的最小值为 ▲ .
26. 【提出定义】已知y是x的函数,当时,函数值;当时,函数值 , 若(i为正整数),则称为该函数的i倍区间.如,函数中,当时, , 当时, , , 所以是函数的3倍区间.(1)、【理解内化】若是函数的i倍区间,则;
(2)、已知是函数(k≠0)的i倍区间(i为正整数),点、是函数(k≠0)图象上的两点.①试说明:;
②当 , 时,求的面积;
(3)、【拓展应用】已知是函数的3倍区间,在此区间内,该函数的最大值与最小值的差为 , 求a、k的值.