江苏省淮安市2022-2023学年八年级下册数学期末试卷

试卷更新日期：2023-08-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下面四个图形分别是节水、回收和绿色食品、低碳标志，在这四个标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 等腰三角形的两边分别为3和6，则这个三角形的周长是（）

A、9 B、12 C、15 D、12或15

查看试题解析
3. $16$ 的平方根是（）

A、 $4$ B、 $- 4$ C、 $8$ D、 $\pm 4$

查看试题解析
4. 关于 $\sqrt{13}$ 的叙述错误的是（）

A、 $\sqrt{13}$ 是无理数 B、在数轴上存在表示 $\sqrt{13}$ 的点 C、 $\sqrt{13} = \sqrt{4} + \sqrt{9}$ D、 $\sqrt{13} > 3$

查看试题解析
5. 如图，在一个直角三角形中，要求用圆规和直尺作图，把它分成两个三角形，其中一个三角形是等腰三角形，其作法不一定正确的是（）

A、 B、 C、 D、

查看试题解析
6. 如图， $A D$ 是 $△ A B C$ 的角平分线， $D E ⊥ A B$ ，垂足为 $E$ ，若 $S_{△ A B C} = 8 ， D E = 2 ， A B = 5$ ，则 $A C$ 的长为（） ．

A、 $2$ B、 $3$ C、 $5$ D、 $7$

查看试题解析
7. 如图，在 $△ A B C$ 中，分别以点 $B$ 和点 $C$ 为圆心，大于 $\frac{1}{2} B C$ 长为半径画弧，两弧相交于点 $M$ 、 $N$ ．作直线 $M N$ ，交 $A C$ 于点 $D$ ，交 $B C$ 于点 $E$ ，连接 $B D$ ．若 $A B = 8 ， A C = 12 ， B C = 5$ ，则 $△ A B D$ 的周长为（）

A、 $20$ B、 $17$ C、 $13$ D、 $25$

查看试题解析
8. 甲、乙两位同学放学后走路回家，他们走过的路程s（米）与所用的时间t（分钟）之间的函数关系如图所示．根据图中信息，下列说法错误的是（）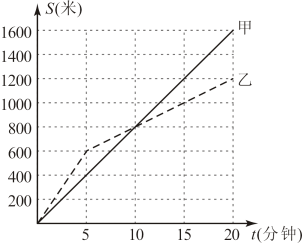

A、前5分钟，甲比乙的速度慢 B、经过20分钟，甲比乙走过的路程少 C、甲的平均速度为80米/分钟 D、经过10分钟，甲、乙都走了800米

查看试题解析

二、填空题

9. 在平面直角坐标系中，点 $P (- 4 ， 3)$ 关于 $y$ 轴对称的点的坐标是．

查看试题解析
10. 点 $A (2 ， y_{1}) ， B (3 ， y_{2})$ 都在一次函数 $y = - x + 2$ 的图像上，则 $y_{1}$ $y_{2}$ （用“ $>$ ”、“ $<$ ”或“ $=$ ”填空）

查看试题解析
11. 将一次函数 $y = 2 x - 6$ 的图像向上平3个单位长度，得到函数的图像．

查看试题解析
12. 弹簧的自然长度为 $5 c m$ ，在弹簧的弹性限度内，所挂的物体的质量x每增加 $1 k g$ ，弹簧的长度y增加 $0.5 c m$ ，则y与x之间的函数关系式是．

查看试题解析
13. 若一个直角三角形的两条直角边长分别为6和8，则它斜边上的中线长为．

查看试题解析
14. 函数 $y = a x + b$ 和 $y = - x + 2$ 的图像如图所示，两图像交于点 $P (- 1 ， m)$ ，则二元一次方程组： ${\begin{array}{l} y - a x = b \\ y + x = 2 \end{array}$ 的解是．

查看试题解析
15. 如图，一次函数 $y = \frac{3}{4} x + 3$ 的图像与x轴、y轴分别交于A、B两点，C是 $O A$ 上的一点，若 $△ A B C$ 将沿 $B C$ 折叠，点A恰好落在y轴上的点 $A^{'}$ 处，则点C的坐标是.

查看试题解析
16. 如图，正方形 $A B C D$ 的边长为6，线段 $E F$ 在边 $B C$ 上左右滑动，若 $E F = 1$ ，则 $A E + D F$ 的最小值为．

查看试题解析

三、解答题

17. 计算：

(1)、 $(π - 3)^{0} - \sqrt{9} \times {(- \frac{1}{2})}^{2}$

(2)、 $(\sqrt{3})^{2} + \sqrt[3]{(- 2)^{3}} - | \sqrt{7} - 3 |$

查看试题解析
18. 求下列各式中的x ．

(1)、 $144 x^{2} = 25$

(2)、 $(x + 1)^{2} = 400$

(3)、 $3 (x - 1)^{3} = 81$

查看试题解析
19. 在平面直角坐标系中 $x O y$ 中，已知点 $M (m - 1 ， 2 m + 6)$ ．

(1)、若点 $M$ 在 $x$ 轴上，求 $m$ 的值；

(2)、若点 $M$ 在第二象限内，求 $m$ 的取值范围．

查看试题解析
20. 在如图所示的正方形网格中，每个小正方形的边长都是 $1$ ， $△ A B C$ 的顶点都在正方形网格的格点（网格线的交点）上．

(1)、 $△ A B C$ 的面积是；

(2)、试利用方格图，用无刻度直尺按要求画图：
①画 $A B$ 边的中线 $C D$ ；

②画线段 $M N$ （ $M 、 N$ 均为格点），使 $M N ⊥ B C$ ．（只画出一条即可）

查看试题解析
21. 如图，点D、E分别是AB、AC的中点，BE、CD相交于点O，∠B＝∠C，BD＝CE.求证：

(1)、OD＝OE；

(2)、△ABE≌△ACD.

查看试题解析
22. 如图，已知 $△ A B C$ ， $C A = C B$ ， $∠ A C D$ 是 $△ A B C$ 的一个外角．

(1)、用尺规作图法，求作直线 $C P$ ，使 $C P ∥ A B$ ；（保留作图痕迹，不写作法，并用2B铅笔描粗）

(2)、请说明（1）中你所作的直线 $C P ∥ A B$ ．

查看试题解析
23. 勾股定理是人类早期发现并证明的重要数学定理之一，是用代数思想解决几何问题的最重要的工具之一，它不但因证明方法层出不穷吸引着人们，更因为应用广泛而使人着迷．

(1)、应用场景1——在数轴上画出表示无理数的点．如图1，在数轴上找出表示2的点A ，过点A作直线l垂直于OA ，在l上取点B ，使 $A B = 1$ ，以原点O为圆心， $O B$ 为半径作弧，则弧与数轴负半轴的交点C表示的数是；

(2)、应用场景2——解决实际问题．如图2，有一个小朋友拿着一根竹竿要通过一个长方形的门，如果把竹竿竖放就比门高出2尺，斜放就恰好等于门的对角线（ $B D$ ），已知门宽6尺，求竹竿长．

查看试题解析
24. 学习“一次函数”时，我们从“数”和“形”两方面研究一次函数的性质，并积累了一些经验和方法．小聪同学尝试运用积累的经验和方法对函数 $y = | x - 1 | - 2$ 的图像与性质进行探究，下面是小聪同学的探究过程，请你补充完整．

(1)、列表：
x
…
$- 2$
$- 1$
0
1
2
3
4
…
y
…
1
0
a
$- 2$
$- 1$
b
1
…
则 $a =$ ， $b =$ ．

(2)、描点并画出该函数的图象；

(3)、①请写出一条关于函数 $y = | x - 1 | - 2$ 的性质：；
②观察函数图象，当 $2 < y < 4$ 时，x的取值范围是；
③观察图像，直接写出函数 $y = | x - 1 | - 2$ 的最小值．

查看试题解析
25. 王老师家、公园、学校依次在同一条直线上，她从家出发匀速步行到公园后，停留 $4 m i n$ ，然后匀速步行到学校．设王老师离公园的距离为y（单位：m），所用时间为x（单位： $m i n$ ），下图表示y与x之间函数关系的图像．

根据图像解答下列问题：

(1)、写出题中的变量：（写两个）：

(2)、①王老师家到学校的距离为 $m$ ；②王老师从家到公园的速度为 $m / m i n$ ；

(3)、求王老师从公园到学校时， $y (m)$ 与 $x (m i n)$ 之间的函数关系式；

(4)、直接写出王老师从家出发 $m i n$ 距离公园 $160 m$ ．

查看试题解析
26. $△ A B C$ 是边长为2的等边三角形，点P是直线 $B C$ 上的一点（不与B、C重合），以 $A P$ 为边向右侧作等边 $△ A P Q$ ，连接 $C Q$ ．

(1)、如图1，点P在边 $B C$ 上．
①请说明： $△ A B P ≌ △ A C Q$ ；
②求出 $△ C P Q$ 周长的最小值；

(2)、当点P在点B的左侧时，在图2中画出符合题意的图形，并直接写出 $C P 、 C Q 、 A C$ 之间的数量关系；

(3)、直接写出当 $△ C P Q$ 为直角三角形时， $B P$ 的长．

查看试题解析
27.

(1)、【情境建模】苏科版教材八年级上册第60页，研究了等腰三角形的轴对称性，我们知道“等腰三角形底边上的高线、中线和顶角平分线重合”，简称“三线合一”．
小明尝试着逆向思考：若三角形一个角的平分线与这个角对边上的高重合，则这个三角形是等腰三角形．即如图1，已知，点D在 $△ A B C$ 的边 $B C$ 上， $A D$ 平分 $∠ B A C$ ，且 $A D ⊥ B C$ ，求证： $A B = A C$ ．请你帮助小明完成证明；

(2)、【理解内化】
请尝试直接应用“情境建模”中小明反思出的结论解决下列问题：
①如图2，在 $△ A B C$ 中， $A D$ 是角平分线，过点B作 $A D$ 的垂线交 $A D$ 、AC于点E、F ， $∠ A B F = 2 ∠ C$ ．求证： $B E = \frac{1}{2} (A C - A B)$ ；
②如图3，在四边形 $A B D C$ 中， $B C = \sqrt{7} ， A C - A B = \sqrt{2}$ ， $A D$ 平分 $∠ C A B ， A D ⊥ C D$ ，当 $△ B C D$ 的面积最大时，请直接写出此时 $C D$ 的长．

(3)、【拓展应用】
如图4， $△ A B C$ 是两条公路岔路口绿化施工的一块区域示意图，其中 $∠ A C B = 90 °$ ， $A C = 30 m$ ， $B C = 40 m$ ，该绿化带中修建了健身步道 $O A 、 O B 、 O M 、 O N 、 M N$ ，其中入口M、N分别在 $A C 、 B C$ 上，步道 $O A 、 O B$ 分别平分 $∠ B A C$ 和 $∠ A B C$ ， $O M ⊥ O A$ ， $O N ⊥ O B$ ．现要用围挡完全封闭 $△ C M N$ 区域，修建地下排水和地上公益广告等设施，试求需要围挡多少m？（步道宽度和接头忽略不计）

查看试题解析

x	…	$- 2$	$- 1$	0	1	2	3	4	…
y	…	1	0	a	$- 2$	$- 1$	b	1	…