江苏省南京市秦淮区六校2022-2023学年八年级下册数学期末试卷

试卷更新日期：2023-08-24 类型：期末考试

进入出卷网下载

一、单选题

1. 如图图形中既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 为了解南京市近十年的降雨量变化情况，最适合用的统计图是（）

A、折线图 B、条形图 C、直方图 D、扇形图

查看试题解析
3. 今年某市有60000名考生参加中考，为了了解这些考生的数学成绩，从中抽取3000名考生的数学成绩进行统计分析．下列说法不正确的是（）

A、每名考生的数学成绩是个体 B、60000名考生数学成绩的全体是总体 C、3000名考生的数学成绩是总体的一个样本 D、样本容量为60000

查看试题解析
4. 菱形具有而平行四边形不一定具有的性质是（）

A、对角相等 B、对角线相等 C、对边平行且相等 D、对角线垂直

查看试题解析
5. 对于函数 $y = - \frac{2}{x}$ ，下列说法错误的是（）

A、它的图象分布在第二、四象限 B、它的图象是中心对称图形 C、y的值随x的增大而增大 D、点 $(- 1 ， 2)$ 是函数图象上的点

查看试题解析
6. 如图，在平行四边形 $A B C D$ 中， $A D = 2 A B = 2$ ， $∠ A B C = 60 °$ ， $E$ ， $F$ 是对角线 $B D$ 上的动点，且 $B E = D F$ ， $M$ ， $N$ 分别是边 $A D$ ，边 $B C$ 上的动点．下列四种说法：
①存在无数个平行四边形 $M E N F$ ；
②存在无数个矩形 $M E N F$ ；
③存在无数个菱形 $M E N F$ ；
④存在无数个正方形 $M E N F$ ．其中正确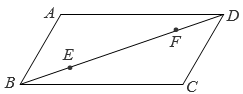的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

7. 计算： $\frac{1}{\sqrt{2}}$ ＝； $\sqrt{12}$ ＝．

查看试题解析
8. 若分式 $\frac{1}{3 x + 1}$ 有意义，则 $x$ 的取值范围是．

查看试题解析
9. 人的呼吸离不开氧气．正常情况下，空气中含氧量为21%左右，在扇形统计图中，表示氧气的扇形圆心角是度．

查看试题解析
10. 若分式 $\frac{2 x^{2}}{x - y}$ 的值为6，当x、y都扩大2倍后，所得分式的值是．

查看试题解析
11. 顺次连接矩形各边中点所得四边形为形．

查看试题解析
12. 反比例函数的图象经过点 $(- 2 ， 8)$ 、 $(a ， - 4)$ 及 $(8 ， b)$ ，则 $a + b =$ ．

查看试题解析
13. 如图所示，数轴上点A所表示的数是a ，化简 $\sqrt{{(a - 1)}^{2}}$ 的结果为．

查看试题解析
14. 若分式方程 $\frac{1}{x - 2} + 1 = \frac{a - x}{x - 2}$ 有增根，则 $a$ 的值是．

查看试题解析
15. 如图，正方形 $A B C D$ 和正方形 $C E F G$ 中，点D在 $C G$ 上， $B C = 1$ ， $C E = 3$ ， H是 $A F$ 的中点，那么 $C H$ 的长为．

查看试题解析
16. 如图，正比例函数 $y_{1} = \sqrt{3} x$ 与反比例函数 $y_{2} = \frac{k}{x} (x > 0)$ 的图像交于点A，另有一次函数 $y = - \sqrt{3} x + b$ 与 $y_{1}$ 、 $y_{2}$ 图像分别交于B、C两点（点C在直线 $O A$ 的上方），且 $O B^{2} - B C^{2} = \frac{16}{3}$ ，则 $k =$ .

查看试题解析

三、解答题

17. 解下列方程

(1)、 $\frac{3}{x} = \frac{2}{x - 2}$ ；

(2)、 $\frac{3}{x - 1} - \frac{x + 2}{x (x - 1)} = 0$ ．

查看试题解析
18. 计算

(1)、 $\sqrt{8 a} \cdot \sqrt{2 a^{5}} (a > 0)$

(2)、 $\sqrt{6} \times (2 \sqrt{3} - 3 \sqrt{\frac{1}{3}})$

查看试题解析
19. 先化简，再求值． $(1 - \frac{1}{a + 1}) \div \frac{a^{2}}{a^{2} - 1}$ ，其中 $a = - 3$ ．

查看试题解析
20. 如图， $▱ A B C D$ 的对角线 $A C$ ， $B D$ 相交于点O ，将对角线 $B D$ 向两个方向延长，分别至点E和点F ，且使 $B E = D F$ ．

(1)、求证：四边形 $A E C F$ 是平行四边形；

(2)、若 $O F = O A$ ，求证：四边形 $A E C F$ 是矩形．

查看试题解析
21. 为了响应国家提出的“每天锻炼1小时”的号召，某校积极开展了形式多样的“阳光体育”运动，小红对该班同学参加锻炼的情况进行了统计，（每人只能选其中一项）并绘制了下面的两幅统计图，请根据图中提供的信息解答下列问题：

(1)、小红这次一共调查了多少名学生？

(2)、通过计算补全条形统计图．

(3)、若该校有2000名学生，请估计该校喜欢乒乓球的学生约有多少人？

查看试题解析
22. 如图，在△ABC中，D是AB边上一点，且BC＝BD ．按下列要求完成尺规作图（保留作图痕迹，不写作法，请标明字母）．

⑴作∠ABC的角平分线交CD于点E；

⑵作线段AD的垂直平分线交AD于点F；

⑶连接EF ，直接写出线段EF和AC的数量关系及位置关系．

查看试题解析

23. 在一只不透明的口袋里，装有若干个除了颜色外均相同的小球，某数学学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复.下表是活动进行中的一组统计数据：

摸球的次数 $n$	100	150	200	500	800	1000
摸到白球的次数 $m$	59	96	$b$	295	480	601
摸到白球的频率 $\frac{m}{n}$	$a$	0.64	0.58	0.59	0.60	0.601

(1)、上表中的

a =

，

b =

；

(2)、“摸到白球的”的概率的估计值是（精确到0.1）；

(3)、如果袋中有12个白球，那么袋中除了白球外，还有多少个其它颜色的球？

查看试题解析

24. 如图，一次函数 $y = x + m$ 的图象与反比例函数 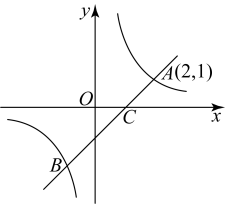$y = \frac{k}{x}$ 的图象交于 $A$ ， $B$ 两点，且与 $x$ 轴交于点 $C$ ，点 $A$ 的坐标为 $(2 ， 1)$ ，点 $B$ 的横坐标为 $- 1$ ．

(1)、求 $m$ 及 $k$ 的值；

(2)、连接 $O A$ ， $O B$ ，求 $△ A O B$ 中 $A B$ 边上的高；

(3)、结合图象直接写出不等式 $x + m \geq \frac{k}{x}$ 的解集．

查看试题解析
25. 某公司研发1000件新产品，需要精加工后才能投放市场．现在甲、乙两个工厂加工这批产品，已知甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天，而乙工厂每天加工的件数是甲工厂每天加工件数的 $1.25$ 倍，公司需付甲工厂加工费用每天100元，乙工厂加工费用每天125元．

(1)、甲、乙两个工厂每天各能加工多少件新产品？

(2)、两个工厂同时合作完成这批产品，共需付加工费多少元？

查看试题解析
26. 数学课上老师让学生们折矩形纸片．由于折痕所在的直线不同，折出的图形也不同，所以各个图形中所隐含的“基本图形”也不同．我们可以通过发现基本图形，来研究这些图形中的几何问题．

(1)、问题解决：
如图1，将矩形纸片 $A B C D$ 沿直线 $M N$ 折叠，使得点 $C$ 与点 $A$ 重合，点 $D$ 落在点 $D_{1}$ 的位置，连接 $M C ， A N ， A C$ ，线段 $A C$ 交 $M N$ 于点 $O$ ，则：

① $△ C D M$ 与 $△ A D_{1} M$ 的关系为，线段 $A C$ 与线段 $M N$ 的关系为，小强量得 $∠ M N C = 50 °$ ，则 $∠ D A N =$ ．

②小丽说：“图1中的四边形 $A N C M$ 是菱形”，请你帮她证明．

(2)、拓展延伸：
如图2，矩形纸片 $A B C D$ 中， $B C = 2 A B = 6 c m ， B M = 4 c m$ ，小明将矩形纸片 $A B C D$ 沿直线 $A M$ 折叠，点 $B$ 落在点 $B_{1}$ 的位置， $M B_{1}$ 交 $A D$ 于点 $N$ ，请你直接写出线段 $N D$ 的长：．

(3)、综合探究：
如图3， $A B C D$ 是一张矩形纸片， $A D = 1 ， A B = 5$ ，在矩形 $A B C D$ 的边 $A B$ 上取一点 $M$ （不与 $A$ 和 $B$ 点重合），在边 $C D$ 上取一点 $N$ （不与 $C$ 和 $D$ 点重合），将纸片沿 $M N$ 折叠，使线段 $M B$ 与线段 $D N$ 交于点 $P$ ，得到 $△ M N P$ ，请你确定 $△ M N P$ 面积的取值范围．

查看试题解析