江苏省扬州市仪征市2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-24 类型:期末考试
一、单选题
-
1. 下面的图案是中国品牌新能源汽车标志,其中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 二次根式中,的值不能是( )A、 B、1 C、0 D、3. 下列调查中,最适合采用普查方式的是( )A、环保部门调查长江的水质情况 B、调查五一期间到扬州旅游的游客满意度 C、调查我市中学生使用手机的时长 D、调查神舟飞船各零件部位是否正常4. 分式 可变形为( )
2. 二次根式中,的值不能是( )A、 B、1 C、0 D、3. 下列调查中,最适合采用普查方式的是( )A、环保部门调查长江的水质情况 B、调查五一期间到扬州旅游的游客满意度 C、调查我市中学生使用手机的时长 D、调查神舟飞船各零件部位是否正常4. 分式 可变形为( )
A、 B、 C、 D、5. 从数学的观点看,对以下成语及诗句中的事件判断正确的是( )A、成语“守株待兔”是随机事件 B、成语“水中捞月”是随机事件 C、诗句“清明时节雨纷纷”是必然事件 D、诗句“离离原上草,一岁一枯荣”是不可能事件6. 已知反比例函数的图象上有两点、 , 如果 , 则实数的取值范围是( )A、 B、 C、 D、或7. 《四元玉鉴》是我国古代数学重要著作之一,为元代数学家朱世杰所著,该著作记载了“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽,每株脚钱三文足,无钱准与一株椽.”大意是:现请人代买一批椽,这批橡的价钱为6210文,如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?(椽,装于屋顶以支持屋顶材料的木杆)设这批椽有株,则符合题意的方程是( )A、 B、 C、 D、8. 如图,直线 , 它们间的距离为2,在直线下方有一定点 , 到的距离为1,点分别是上的动点,平面内一点与三点构成 , 则对角线长度的最小值是( ) A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
9. 如果分式有意义,那么x的取值范围是10. 一个不透明的袋里装有除颜色外其他完全相同的8个小球,其中有4个红球,3个黄球,1个白球,将袋中的球摇匀,从中任意摸出一个球,摸出球的可能性最小.11. 若的值在两个连续整数与之间,则 .12. 某批篮球的质量检验结果如下:
抽取的篮球数
100
200
400
600
800
1000
1200
优等品的频数
93
192
380
561
752
941
1128
优等品的频率
从这批篮球中,任意抽取一只篮球是优等品的概率的估计值是.(精确到 )
13. 如图,把矩形绕点按逆时针方向旋转得到矩形 , 使点落在对角线上,连接 , 若 , 则°. 14. 反比例函数的图象与一次函数的图象交于点 , 则的值是 .15. 如图,已知中, , 于点,为边的中点,若 , , 则的长为 .
14. 反比例函数的图象与一次函数的图象交于点 , 则的值是 .15. 如图,已知中, , 于点,为边的中点,若 , , 则的长为 . 16. 关于x的方程 的解是正数,则a的取值范围是 .17. 定义运算“※”: , 若 , 则的值为 .18. 如图,位于平面直角坐标系中,点B在x轴正半轴上,点A及的中点D在反比例函数的图象上,点C在反比例函数的图象上,则k的值为.
16. 关于x的方程 的解是正数,则a的取值范围是 .17. 定义运算“※”: , 若 , 则的值为 .18. 如图,位于平面直角坐标系中,点B在x轴正半轴上,点A及的中点D在反比例函数的图象上,点C在反比例函数的图象上,则k的值为.
三、解答题
-
19.(1)、计算:;(2)、解方程: .20. 先化简: , 当为整数时,该代数式的值也为整数,请直接写出所有值.21. 为落实双减政策,某学校实行课后延迟服务计划,根据学生的兴趣爱好组建课外兴趣小组,并随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
 (1)、学校这次调查的样本容量是;(2)、在扇形统计图,“围棋”所在扇形的圆心角度数为 , 并补全条形统计图;(3)、设该校共有学生1200名,请你估计该校有多少名学生喜欢书法.22. 已知二次根式 .(1)、求使得该二次根式有意义的的取值范围;(2)、已知是最简二次根式,且与可以合并,
(1)、学校这次调查的样本容量是;(2)、在扇形统计图,“围棋”所在扇形的圆心角度数为 , 并补全条形统计图;(3)、设该校共有学生1200名,请你估计该校有多少名学生喜欢书法.22. 已知二次根式 .(1)、求使得该二次根式有意义的的取值范围;(2)、已知是最简二次根式,且与可以合并,求的值;
求与的乘积.
23. 小明用元买软面笔记本,小丽用元买硬面笔记本.已知每本硬面笔记本比软面笔记本贵元.(1)、设软面笔记本每本元,则小丽买硬面笔记本本;(2)、小明和小丽能买到相同数量的笔记本吗?24. 如图,点E、F分别在▱ABCD的边AB、CD的延长线上,且BE=DF,连接AC、EF、AF、CE,AC与EF交于点O.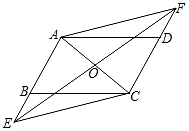 (1)、求证:AC、EF互相平分;(2)、若EF平分∠AEC,求证:四边形AECF是菱形.25. 如图,平行于轴的直尺(一部分)与双曲线交于点和 , 与轴交于点和 , 直尺的宽度为 , , .
(1)、求证:AC、EF互相平分;(2)、若EF平分∠AEC,求证:四边形AECF是菱形.25. 如图,平行于轴的直尺(一部分)与双曲线交于点和 , 与轴交于点和 , 直尺的宽度为 , , . (1)、求反比例函数解析式;(2)、若经过两点的直线关系式为 , 请直接写出不等式的解集;(3)、连接、 , 求的面积.26. 如图,已知正方形为上任意一点,请仅用无刻度的直尺完成下列作图,不写作法,保留作图痕迹.(用虚线表示画图过程,实线表示画图结果)
(1)、求反比例函数解析式;(2)、若经过两点的直线关系式为 , 请直接写出不等式的解集;(3)、连接、 , 求的面积.26. 如图,已知正方形为上任意一点,请仅用无刻度的直尺完成下列作图,不写作法,保留作图痕迹.(用虚线表示画图过程,实线表示画图结果) (1)、在边上找点 , 使得直线将正方形的面积平均分成相等的两部分;(在图1中完成)(2)、在边上找点 , 使得;(在图2中完成)(3)、连接 , 将绕点逆时针旋转 , 作出旋转后的三角形.(在图3中完成)27. 定义:若分式与分式的差等于它们的积,即 , 则称分式是分式“友好分式”.
(1)、在边上找点 , 使得直线将正方形的面积平均分成相等的两部分;(在图1中完成)(2)、在边上找点 , 使得;(在图2中完成)(3)、连接 , 将绕点逆时针旋转 , 作出旋转后的三角形.(在图3中完成)27. 定义:若分式与分式的差等于它们的积,即 , 则称分式是分式“友好分式”.如与 , 因为 , ,
所以是的“友好分式”.
(1)、分式分式的“友好分式”(填“是”或“不是”);(2)、小明在求分式的“友好分式”时,用了以下方法:设的“友好分式”为 , 则 ,
∴ ,
∴ .
请你仿照小明的方法求分式的“友好分式”.
(3)、①观察(1)(2)的结果,寻找规律,直接写出分式的“友好分式”: .②若是的“友好分式”,则的值为 .
28. 如图1所示,有公共顶点的两个正方形和正方形 , , , 将正方形绕点在平面内任意旋转.
 (1)、发现:
(1)、发现:①线段之间的数量关系是;
②直线之间的位置关系是;
(2)、①如图2,连接、、 , 分别取三条线段的中点、、 , 判断的形状并说明理由;②当时,求出面积的取值范围;
(3)、设点、到点的距离分别为、 , 直接写出的最小值.